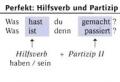
Bessel-függvények. Tanfolyam: Bessel-függvények A Bessel-függvény grafikonja

Megrendelések.

Habár $\backslash alpha$És $(-\backslash alfa)$ azonos egyenleteket generálnak, általában megegyeznek abban, hogy különböző függvények felelnek meg nekik (ezt pl. azért teszik, hogy a Bessel-függvény sima legyen $\backslash alpha$).

A Bessel-függvényeket először Daniel Bernoulli svájci matematikus határozta meg, és Friedrich Besselről nevezték el.

Alkalmazások

A Bessel-egyenlet akkor merül fel, amikor a Laplace-egyenletre és a Helmholtz-egyenletre hengeres és gömbkoordinátákban keresünk megoldást. Ezért a Bessel-függvényeket számos hullámterjedés, statikus potenciál stb. probléma megoldására használják, például:

• elektromágneses hullámok hengeres hullámvezetőben;
• hővezető képesség hengeres tárgyakban;
• vékony kerek membrán vibrációs módjai;
• kör alakú lyukkal elhajló fény intenzitáseloszlása;
• a részecskék sebessége egy folyadékkal töltött és a tengelye körül forgó hengerben;
• hullámfüggvények gömbszimmetrikus potenciáldobozban.

A Bessel-függvényeket más problémák megoldására is használják, például a jelfeldolgozásban.

Definíciók

Mivel a fenti egyenlet egy másodrendű lineáris differenciálegyenlet, két lineárisan független megoldással kell rendelkeznie. A körülményektől függően azonban ezeknek a döntéseknek különböző definícióit választják. Az alábbiakban ezek közül mutatunk be néhányat.

Az első típusú Bessel-függvények

Az első típusú Bessel-függvények, jelölve $J\_\backslash alpha(x)$, a megoldások végesek a pontban $x=0$ egész vagy nem negatív $\backslash alpha$. Egy adott függvény kiválasztását és normalizálását annak tulajdonságai határozzák meg. Ezeket a függvényeket a Taylor sorozat nulla körüli kiterjesztésével (vagy egy általánosabb hatványsorral a nem egész számokhoz) definiálhatjuk $\backslash alpha$):

$J\_\backslash alpha(x)\; =\; \backslash sum\_(m=0)^\backslash infty\; \backslash frac((-1)^m)(m!\backslash ,\; \backslash Gamma(m+\backslash alpha+1))\; (\backslash left((\backslash frac()\; x)(2))\backslash jobbra))^(2m+\backslash alfa)$

A Neumann-függvényeket másodlagos Bessel-függvényeknek is nevezik. Az első és a második típusú Bessel-függvények lineáris kombinációja a Bessel-egyenlet teljes megoldása:

$y(x)\; =\; C\_1\; J\_\backslash alpha(x)\; +\; C\_2\; Y\_\backslash alpha(x).$

Alul látható a grafikon $Y\_\backslash alpha\; (x)$ Mert $\backslash alpha\; =\; 0$, 1 és 2:

Tulajdonságok

Ortogonalitás

Hadd $\backslash mu\_1$És $\backslash mu\_2$- a Bessel-függvény nullái $J\_(\backslash alpha)(x)$. Akkor :

$\backslash int\_(0)^(1)(x\; J\_(\backslash alpha)(\backslash mu\_1\; x)\; J\_(\backslash alpha)(\backslash mu\_2\; x)\; dx)\; =\; \backslash left\backslash (\; \backslash begin(mátrix)$

0 & \mbox(;)\quad\mu_1\ne\mu_2 \\ \\ \frac(1)(2)(J"_(\alpha)(\mu_1))^2 & \mbox(;)\quad \mu_1=\mu_2

\end(mátrix) \jobbra. .

Aszimptotikumok

Az aszimptotikus képletek az első és a második típusú Bessel-függvényekre ismertek. Kisebb vitákhoz és nem negatív $\backslash alpha$így néznek ki:

$J\_\backslash alpha(x)\; \backslash rightarrow\; \backslash frac(1)(\backslash Gamma(\backslash alpha+1))\; \backslash left(\backslash frac(x)(2)\; \backslash right)\; ^\backslash alpha\; ,$

\end(mátrix) \jobbra. ,

$J\_\backslash alpha(z)=\backslash frac((z/2)^\backslash alpha)(\backslash Gamma(\backslash alpha+1))\; ()\_0F\_1\; (\backslash alpha+1;\; -z^2/4).$

Így egész számokra $\backslash alpha$ Bessel-függvény egyértelmű elemző, és a nem egész számokhoz - többértékű analitikus.

Generáló funkció

Létezik az első típusú és egész rendű Bessel-függvények reprezentációja egy bizonyos típusú függvény Laurent-sorának együtthatóin keresztül, nevezetesen:

$e^(\backslash frac(z)(2)\backslash left(w-\backslash frac(1)(w)\backslash right))=\backslash sum\_(n=-\backslash infty)^(+\backslash infty)J\_n(z)w^\; n.$

Arányok

Jacobi-Anger formula és kapcsolódó

Kifejezéseket kapunk az at generáló tényezőhöz $a=1$, $t=e^(i\backslash phi)$:

$e^(iz\backslash sin\backslash phi)=J\_0(z)+2\backslash sum\_(n=1)^\backslash infty\; J\_(2n)(z)\backslash cos(2n\backslash phi)+2i\backslash sum\_(n=1)^\; \backslash infty\; J\_(2n-1)(z)\backslash sin(2n-1)\backslash phi.$

Nál nél $a=1$, $t=ie^(i\backslash phi)$:

$e^(iz\backslash cos\backslash phi)=J\_0(z)+2\backslash sum\_(n=1)^\backslash infty\; i^nJ\_n(z)\backslash cos(n\backslash phi).$

Összeadás tétel

Bármilyen egészhez $n$és összetett $z\_1$És $z\_2$ teljesített

$J\_n(z\_1+z\_2)\; =\; \backslash sum\_(k=-\backslash infty)^\backslash infty\; J\_k(z\_1)\; J\_(n-k)(z\_2).$

Integrál kifejezések

Bármilyen $a$És $b$(beleértve a komplexet is) végzik

$\backslash int\_0^\backslash infty\; e^(-at)J\_n(bt)\backslash mathrm\; dt\; =\; \backslash frac(b^n)(\backslash sqrt(a^2+b^2)(\backslash sqrt(a^2+b^2)\; +a)^n).$

Az utolsó képlet speciális esete a kifejezés

$\backslash int\_0^\backslash infty\; e^(-at)J\_0(bt)\backslash mathrm\; dt\; =\; \backslash frac(1)(\backslash sqrt(a^2+b^2)).$

Lásd még

Írjon véleményt a "Bessel-függvények" című cikkről

Megjegyzések

Irodalom

• Watson G. A Bessel-függvények elmélete. - M.: IL, 1949.
• Bateman G., Erdelyi A. Bessel-függvények, parabolikus hengerfüggvények, ortogonális polinomok // Magasabb transzcendentális függvények. T. 2. 2. kiadás / Ford. angolról N. Ya. Vilenkina. - M.: Nauka, 1974. - 296 p.
• Lavrentiev M. A., Shabat B. V. Egy komplex változó függvényelméletének módszerei. - M.: Nauka, 1973. - 736 p.

A Bessel-függvényeket jellemzõ részlet

– Vera – szólt a grófnő legidősebb lányához, akit nyilvánvalóan nem szeretett. - Hogyhogy fogalmad sincs semmiről? Nem érzed úgy, hogy nincs itt a helyed? Menj a nővéreidhez, vagy...
A gyönyörű Vera megvetően mosolygott, láthatóan a legcsekélyebb sértést sem érezte.
– Ha már régen elmondtad volna, anya, azonnal elmentem volna – mondta, és felment a szobájába.
De a kanapé mellett elhaladva észrevette, hogy két pár szimmetrikusan ül két ablaknál. Megállt, és megvetően elmosolyodott. Sonya közel ült Nyikolajhoz, aki verseket másolt neki, amelyeket először írt. Borisz és Natasa egy másik ablaknál ültek, és elhallgattak, amikor Vera belépett. Sonya és Natasha bűntudatos és boldog arccal nézett Verára.
Szórakoztató és megható volt nézni ezeket a szerelmes lányokat, de a látványuk nyilván nem keltett kellemes érzést Verában.
– Hányszor kértelek – mondta –, hogy ne vigye el a cuccaimat, saját szobája van.
Nyikolajtól átvette a tintatartót.
– Most, most – mondta, és megnedvesítette a tollat.
– Tudod, hogyan kell mindent rosszkor csinálni – mondta Vera. – Aztán beszaladtak a nappaliba, így mindenki szégyellte magát miattad.
Annak ellenére, hogy vagy éppen azért, mert teljesen igazságos volt, amit mondott, senki nem válaszolt neki, és mind a négyen csak egymásra néztek. A tintatartóval a kezében elidőzött a szobában.
- És milyen titkok lehetnek a te korodban Natasa és Borisz között, valamint közted - ezek mind ostobaságok!
- Nos, mit érdekel, Vera? – szólt közbe Natasha halk hangon.
Úgy látszik, aznap még kedvesebb és ragaszkodóbb volt mindenkivel, mint mindig.
– Nagyon hülye – mondta Vera –, szégyellem magát. Mik a titkok?...
- Mindenkinek megvan a maga titka. Nem érintünk meg téged és Berget – mondta Natasha izgatottan.
– Azt hiszem, nem fogsz hozzám nyúlni – mondta Vera –, mert soha nem lehet semmi rossz a tetteimben. De elmondom anyucinak, hogyan bánsz Borisszal.
„Natalja Iljinisna nagyon jól bánik velem” – mondta Borisz. – Nem panaszkodhatok – mondta.
- Hagyd, Borisz, te olyan diplomata vagy (a diplomata szót nagyon használták a gyerekek körében abban a különleges jelentésben, amit ehhez a szóhoz tulajdonítottak); Még unalmas is – mondta Natasha sértett, remegő hangon. - Miért zaklat engem? Ezt soha nem fogod megérteni – mondta Verához fordulva –, mert soha nem szerettél senkit; nincs szíved, csak madame de Genlis [Madame Genlis] vagy (ezt a nagyon sértőnek tartott becenevet Nyikolaj adta Verának), és az első örömöd, hogy bajt okozol másoknak. – Amennyit csak akarsz, flörtölsz Berggel – mondta gyorsan.
- Igen, biztosan nem kezdek majd üldözni egy fiatalembert a vendégek előtt...
– Nos, elérte a célját – szólt közbe Nyikolaj –, mindenkinek kellemetlen dolgokat mondott, mindenkit feldúlt. Menjünk a gyerekszobába.
Mind a négyen, mint egy riadt madárcsapat, felkeltek, és elhagyták a szobát.
„Mondtak néhány problémát, de nem jelentettem senkinek semmit” – mondta Vera.
- Madame de Genlis! Madame de Genlis! - szóltak nevető hangok az ajtó mögül.
A szépséges Vera, aki olyan irritáló, kellemetlen hatással volt mindenkire, mosolygott, és láthatóan nem befolyásolva a neki elmondottakat, a tükörhöz lépett és megigazította a sálját és a frizuráját. Gyönyörű arcára nézve láthatóan még hidegebb és nyugodtabb lett.

A beszélgetés a nappaliban folytatódott.
- Ah! chere - mondta a grófnő -, és az életemben tout n"est pas rose. Hát nem látom, hogy du train, que nous allons, [nem minden rózsa. - életvitelünkből adódóan] állapotunk nem fog sokáig tart nekünk! És "Ez mind egy klub, és a kedvessége. Faluban élünk, tényleg pihenünk? Színházak, vadászat és Isten tudja, mit. De mit mondjak rólam! Nos, hogyan intézted el az egészet Gyakran meglepődök rajtad, Annette, hogy lehetséges, hogy te, a te korodban egyedül utazol egy hintón, Moszkvába, Szentpétervárra, minden miniszterhez, minden nemességhez, tudod, hogyan juthatsz el mindenkivel együtt, én is meglepődtem! Nos, ez hogy sikerült? Nem tudom, hogyan kell ezt csinálni.
- Ó, lelkem! - válaszolta Anna Mihajlovna hercegnő. – Adja Isten, hogy tudja, milyen nehéz özvegynek maradni tartás nélkül, és egy fiával, akit imádásig szeretsz. – Mindent megtanulsz – folytatta némi büszkén. – A folyamatom megtanított. Ha látnom kell egyet ezek közül az ászok közül, írok egy megjegyzést: „hercegnő une telle [az-az-az hercegnő] ezt-azt akar látni”, és legalább kettőt, legalább egy taxit vezetek. háromszor, legalább négyszer, amíg elérem, amire szükségem van. Nem érdekel, hogy ki mit gondol rólam.
- Nos, hát kit kérdeztél Borenkaról? – kérdezte a grófné. - Végül is a tied már őrtiszt, Nikolushka pedig kadét. Nincs kit zavarni. kit kérdeztél?
- Vaszilij herceg. Nagyon kedves volt. Most mindenbe beleegyeztem, jelentettem a szuverénnek” – mondta elragadtatva Anna Mihajlovna hercegnő, teljesen megfeledkezve arról a megaláztatásról, amelyet célja elérése érdekében átélt.
- Hogy megöregedett, Vaszilij herceg? – kérdezte a grófné. – A Rumjantsevok színháza óta nem láttam. És azt hiszem, megfeledkezett rólam. „Il me faisait la cour, [Utánam jött” – emlékezett vissza mosolyogva a grófnő.
- Még mindig ugyanaz - válaszolta Anna Mihajlovna -, kedves, omlós. Les grandeurs ne lui ont pas touriene la tete du tout. [A magas beosztás egyáltalán nem forgatta fel a fejét.] „Sajnálom, hogy túl keveset tehetek érted, drága hercegnőm – mondja –, rendet. Nem, ő egy kedves ember és egy csodálatos családtag. De tudod, Nathalieie, szerelmem a fiam iránt. Nem tudom, mit ne tennék, hogy boldoggá tegyem. - És a körülményeim olyan rosszak - folytatta Anna Mihajlovna szomorúan és lehalkítva a hangját -, olyan rosszak, hogy most a legszörnyűbb helyzetben vagyok. Az én nyomorúságos folyamatom az, hogy felfalok mindent, amim van, és nem mozdulok. Elképzelheti, hogy nincs a la lettre-em [szó szerint], egy fillér pénzem sincs, és nem tudom, mivel öltöztessem fel Borist. „Elővett egy zsebkendőt, és sírni kezdett. – Ötszáz rubelre van szükségem, de van egy huszonötrubeles bankjegyem. Ebben a helyzetben vagyok... Az egyetlen reményem most Kirill Vlagyimirovics Bezukhov gróf. Ha nem akarja eltartani a keresztfiát - elvégre ő keresztelte meg Borját -, és kijelölni neki valamit a fenntartására, akkor minden bajom elvész: nem lesz mivel felszerelni.
A grófné könnyeket hullatott, és némán gondolkozott valamin.
„Gyakran arra gondolok, talán ez bűn – mondta a hercegnő –, és gyakran arra gondolok: Kirill Vlagyimirovics Bezuhoj gróf egyedül él... ez hatalmas vagyon... és minek él? Az élet teher számára, de Borya csak most kezd élni.
– Valószínűleg hagy valamit Borisznak – mondta a grófnő.
- Isten tudja, chere amie! [kedves barátom!] Annyira önzőek ezek a gazdag emberek és nemesek. De most is elmegyek hozzá Borisszal, és egyenesen elmondom neki, hogy mi a helyzet. Hadd gondoljanak rólam, amit akarnak, tényleg nem érdekel, hogy mikor múlik rajta a fiam sorsa. - A hercegnő felállt. - Most két óra van, és négy órakor ebédelsz. lesz időm menni.
És egy szentpétervári üzletasszony technikájával, aki tudja, hogyan kell használni az időt, Anna Mihajlovna elküldte a fiát, és kiment vele a hallba.
- Viszlát, lelkem - mondta a grófnőnek, aki az ajtóig kísérte -, kívánok sok sikert - tette hozzá fia suttogva.
– Meglátogatja Kirill Vladimirovics grófot, ma chere? - mondta a gróf az ebédlőből, és szintén kiment a folyosóra. - Ha jobban érzi magát, hívd meg Pierre-t velem vacsorázni. Hiszen meglátogatott és táncolt a gyerekekkel. Mindenképpen hívj, ma chere. Nos, lássuk, hogyan tünteti ki magát Taras ma. Azt mondja, hogy Orlov grófnak soha nem volt olyan vacsorája, mint nálunk.

A Bessel-differenciálegyenlet egy valós szám, ahol és alakú egyenlet. Ennek az egyenletnek szinguláris pontja z = 0 (a (7) legmagasabb deriváltjának együtthatója x = 0-nál eltűnik). Az (5) és (7) összehasonlításból arra a következtetésre jutunk, hogy a Bessel-egyenletre úgy, hogy x = 0 a Po(x) függvény másodrendű nullája (m = 2), a p\ függvény elsőrendű nullája. (x) és nem a pi (x) függvény nullája (ha v Ф 0). Ezért a 17. Tétel értelmében a (7) egyenletnek van egy megoldása egy általánosított hatványsor formájában, ahol a a meghatározandó karakterisztikus kitevő. Írjuk át a (8) kifejezést alakra Bessel-egyenlet Bessel-függvények Differenciálegyenlet Euler G-függvénye és tulajdonságai Félegész index Bessel-függvényeinek ismétlődési képletei Bessel-függvények nullái Ortogonalitás és norma Neumann (Weber) függvények és keressük meg a deriváltokat: Helyettesítsük be ezeket kifejezéseket a (7) egyenletbe, és nullával egyenlővé téve x együtthatóit a hatványhoz kapunk egyenletrendszert, akkor az első (9) egyenletből az következik, hogy vagy Most a második (9) egyenletből lesz. először mérlegelje az esetet. Írjuk át a (9) rendszer egyenletét olyan alakban, amelyből ak-2-n keresztül egy ismétlődő képletet kapunk ak meghatározására".) Tekintettel arra, hogy innen a3 = 0 és általában Másrészt minden páros együttható az előzővel fejezhető ki a képlet segítségével A képlet egymást követő alkalmazása lehetővé teszi, hogy megtaláljuk az a2m kifejezést ao-n keresztül: Helyettesítsük be az együtthatók talált értékeit a (8), (10) képletbe. annak ellenőrzésére, hogy a (10) jobb oldalán lévő sorozat az x > 0 féltengelyen konvergál, és ott határozza meg a függvény(eke)t - a Bessel-egyenlet egy sajátos megoldása. Tekintsük most a második esetet, amikor a = -u Ha v nem egyenlő egy pozitív egész számmal, akkor írhatunk egy második parciális megoldást, amelyet a (10) kifejezésből kapunk úgy, hogy v-t -v-re cseréljük (v egyenletesen jelenik meg a (7) egyenletben), (“O ( Ha és egyenlő egy pozitív egész számmal, akkor a (101) megoldás érvényét veszti, mivel egy bizonyos számból kiindulva az (1(Y)) bővítési tagok nevezőjében szereplő egyik tényező nulla lesz. a jobb oldali sorozat (10”) is konvergál minden x > 0 értékre. Az yi(x) és y2(x) megoldások lineárisan függetlenek. Valójában kapcsolatuk nem állandó. 12.2. Euler G-függvénye és tulajdonságai A következőkhöz szükségünk lesz az Euler-féle G-függvény néhány tulajdonságára. A következőképpen definiálható: Részenkénti integrálással megkapjuk a G-függvény fő funkcionális egyenletét: Mivel és általában Az is kimutatható, hogy a (11) funkcionális egyenlet segítségével meghatározható a gammafüggvény negatív értékekre az érvről. Miután a (11) egyenletet Г(р) = alakban írtuk fel, megjegyezzük, hogy kis р esetén a Г(р) ~ £ összefüggés áll fenn. Hasonlóképpen, ha m egy pozitív egész szám, akkor az -m számhoz közeli p értékek esetén kimutatható, hogy Γ(p) Φ 0 bármely p-re, ezért az u függvény minden értékre folytonos lesz. p-ből, ha visszatérünk a (7) Bessel-egyenlet megoldásához. Az oq együttható eddig önkényes maradt. Ha v Ф -п, ahol n > 0 egy egész szám, akkor feltéve, hogy ezt a kifejezést behelyettesítjük a (9) együtthatókba, azt kapjuk, hogy a (12) sorozat egy függvényt definiál, amely a Bessel-egyenlet megoldása, és az ún. az első típusú és a harmadrendű Bessel-függvény. A sorozat megfelel az a = -u esetnek (és nem egész), és meghatározza a (7) egyenlet második megoldását, lineárisan független a So függvénnyel, ha v nem egyenlő az egész számmal (, akkor a Jv( x) és J-v(x) alapvető megoldási rendszert alkotnak a Bessel-egyenlet (7) és általános megoldása ebben az esetben V-re az egész lineáris összefüggés fennáll. , mivel a = 1. Az m = k + n jelölést bevezetve azt találjuk, hogy felírjuk az első típusú nulla (n = 0) és első (n = 1) sorrendű Bessel-függvények sorozatát: A Jb( x) és J\ (x) (4. ábra) gyakran megtalálhatók az alkalmazásokban, és ezekhez részletes táblázatok is találhatók 12.4 Bessel-függvények ismétlődési képlete A képlet közvetlen ellenőrzésével meg vagyunk győződve arról, hogy Pontosan ugyanazt a számítást találjuk Bővítés a (15) és a (16) képlet bal oldalán lévő szorzatok származékait, megkapjuk az egyenlőségeket, a (17) és (18) összeadásával és kivonásával két fontos ismétlődő képletet kapunk: A (19) képlet azt mutatja, hogy a A Bessel-függvények deriváltjait Bessel-függvények fejezik ki. A (20) képletből az következik, hogy Jv(x) és Jv-\(x) ismeretében megtalálhatjuk (/1/+\(x). Konkrétan az egész számok összes Bessel-függvényét két Jo függvény fejezi ki. (x) és J\(x)- Itt a (14) reláció bizonyul hasznosnak, 1/ = 1-re (20)-ból például 12.5. Félegész indexű Bessel-függvények Tekintsünk egy speciális osztályt A páratlan egész szám felével egyenlő indexű Bessel-függvények Ez az osztály az alkalmazásokban fordul elő, és figyelemre méltó, hogy a vizsgált esetben a Bessel-függvények elemi függvényekkel fejezhetők ki, így u = I esetén egyszerű transzformációkkal Hasonlóképpen, mert megkapjuk Mindkét képlet felírható a következő formában: Egyenlet Bessel-függvények Differenciálegyenlet Euler Г-függvénye és tulajdonságai Félegész indexű Bessel-függvények ismétlődő képletei Bessel-függvények nullai Ortogonalitás és norma Neumann (Weber) funkciók 12. 6. A Bessel-függvények nullái Sok alkalmazott probléma megoldása során szükség van a Bessel-függvények nullák eloszlására vonatkozó elképzelésre. A függvények és J-x^x) nullai egybeesnek sin x és cos x nulláival. Megmutatható, hogy x nagy értékeire létezik egy aszimptotikus ábrázolás1* (hasonlítsa össze, mi érvényes egész és tört számra is. A (22) képlet megmutatja, hogyan viselkedik a Bessel-függvény az argumentum növekedésével. Ez egy oszcilláló függvény amely nullává változik, és az oszcillációk amplitúdója nullára hajlik, mint x -» +oo. A pozitív egész indexű Bessel-függvény nulláinak eloszlását, azaz az egyenlet gyökét a következő tétel határozza meg. 18. A függvénynek nincsenek összetett nullái, de van egy végtelen halmaza valódi nulláknak, amelyek szimmetrikusan helyezkednek el az x = 0 ponthoz képest, amely n = 1,2,... esetben ezek egyike. függvények egyszerűek, kivéve az x = 0 pontot, amely n = 1,2,... esetén az n multiplicitás nulla. Könnyen ellenőrizhető, hogy a (23) egyenletet a Jv(\x) Bessel-függvény teljesíti. Írjuk át a (23) egyenletet alakba, és jelöljük - az A paraméter tetszőleges értékét. Ekkor megkapjuk az azonosságokat. Az első azonosságot megszorozva a másodikkal -) és kivonva egyiket a másikból, megkapjuk az összes szorzást. az utolsó azonosság feltételei w-vel, megjegyezzük, hogy felírható a következő alakban Ha az utolsó azonosságot x felett a 0-tól 1-ig terjedő tartományba integráljuk, akkor (25) egyenlőségeink lesznek, ebből következik, hogy ha Ai, Ar nullai a függvény, akkor a (25) bal oldala, tehát a jobb oldala nullával egyenlő, tehát Ez a definíció szerint azt jelenti, hogy a függvények p(x) = x súllyal merőlegesek egy p 3 súlyú szakaszon. Legyen A|, Ar annak az egyenletnek a gyöke, ahol h valamilyen rögzített szám. A (28) egyenlet megtalálható a matematikai fizikában, és v > -1 esetén végtelen sok pozitív gyöke van, de nincs összetett gyöke (kivéve azt az esetet, amikor két tisztán képzeletbeli gyök van). Miután a (25) egyenlőség bal oldalát a formába írtuk, meggyőződtünk a Bessel-függvények ortogonalitásáról a Bessel-függvény xJu(x) - hji,(x) = 0 lineáris kombinációjának nullaihoz viszonyítva. származéka: hol vannak a (28) egyenlet gyökei. Bessel-függvények normája Érték 12.8. Neumann (Weber) függvények A Bessel-egyenlet bármely nem triviális megoldását hengerfüggvénynek nevezzük. Ha v nem egész szám, a függvények a (7) Bessel-egyenlet megoldásainak funkcionális rendszerét alkotják. Ha u = n - egész szám, akkor lineáris függőség van, hogy olyan Jr\x) megoldást találjunk, amely nem arányos vele, ezt tesszük: nem egész számra és összeállítjuk a függvényt Ez egy lineáris kombináció a (7) lineáris homogén egyenlet megoldásai közül, és ezért maga is megoldása ennek az egyenletnek. Ha a (30)-t v -» n-ként lépjük át a határértékre, és L'Hopital-szabályt használunk, akkor a J/y\(x) függvények jellegzetes tulajdonságát kapjuk (2. típusú Bessel-függvények) - a szingularitás jelenléte. a koordináták origójában (5. ábra) A (7) Bessel-egyenlet v = n és Jn(x) mellett megtalált megoldása az egyenlet alapvető megoldási rendszerét alkotja. Egyenlet Bessel-függvények Differenciálegyenlet Euler G-függvénye és tulajdonságai Ismétlődés képletek félegész index Bessel-függvényeihez Bessel-függvények nullái Ortogonalitás és norma Neumann-függvények ( Weber) A Λ£(x) függvényt Neumann- vagy Weber-függvénynek is nevezik. Megfelelően nagy x esetén tehát az 1. és 2. típusú hengerfüggvények az origótól nagy távolságban koszinuszként és szinuszként viszonyulnak egymáshoz, de a faktor miatt csökkennek az x növekedésével Ezek a függvények alkalmasak állóhengeres hullámok ábrázolására. Az exponenciális függvényekkel (Euler-képletekkel) analóg módon meg lehet alkotni a Jv(x) függvények lineáris kombinációját, amely a mozgó hullámokhoz kapcsolódó függvényeket adja meg. Így jutunk el a 3. típusú Bessel-függvényekhez vagy a relációkkal definiált Hankel-függvényekhez. Gyakorlatok Keressünk általános megoldást az egyenletekre: Találjunk megoldást a Cauchy-problémára: Integráljuk az egyenleteket, részmegoldásokat keresve a jelzett helyeken: Keressünk általános megoldásokat a következőkre lineáris inhomogén differenciálegyenletek Parciális megoldások típusai Inhomogén lineáris egyenletek állandó együtthatóval különböző jobb oldalakra Differenciálegyenletek jobb oldala*) Karakterisztikus egyenlet gyökerei Konkrét megoldások típusai 1. A 0 nem gyöke a karakterisztikus egyenletnek A 0 szám az r 2 karakterisztikus egyenlet gyöke. Az a szám nem egy karakterisztikus egyenlet gyöke. Az a szám az r 3 karakterisztikus egyenlet gyöke. A ± ""/3 számok nem gyökei a karakterisztikus egyenletnek. a karakterisztikus egyenlet. A ± "/9 számok az r 4 multiplicitás karakterisztikus egyenletének gyökei. Az a ± i/3 számok nem a karakterisztikus egyenlet gyökei. Az a ± i/3 számok a karakterisztikának a gyökei r multiplicitás egyenlete *) A jobb oldalak első három típusa a negyedik speciális esete. Adja meg az alábbi lineáris inhomogén egyenletek részmegoldásának típusát: Az állandók variációs módszerével integrálja a következő egyenleteket: Integrálja a következő Euler-egyenleteket: Válaszok

BESSEL-FUNKCIÓK, 1. típusú hengeres függvények; kör- és hengerszimmetriájú területeken figyelembe vett fizikai folyamatok (hővezetőképesség, diffúzió, rezgések stb.) vizsgálatánál használatosak. A Bessel-függvények a Bessel-egyenlet megoldásai.

Bessel-függvények J p sorrendje (index) p, -∞<р<∞, представляется сходящимся при всех Х рядом

ahol G a gammafüggvény. J p (x) grafikonja x > 0 esetén egy görbe csillapított rezgésekkel; J p (x) végtelen számú nullával rendelkezik; a sorozat első tagjai a J p (x) aszimptotikus kifejezését adják kicsi |x| esetén, nagy x>0 esetén az aszimptotikus reprezentáció érvényes

A p = n + 1/2 rendű Bessel-függvényeket, ahol n egész szám, elemi függvényekkel fejezzük ki; különösen,

µ n p - a J egyenlet pozitív gyökei p (x) = 0, p > - 1/2, l - valamilyen pozitív szám, ortogonális rendszert alkotnak x súllyal a (0, l) intervallumon.

A J 0 függvényt először D. Bernoulli tanulmányozta a nehéz láncok rezgéseivel foglalkozó munkájában (1732). L. Euler, figyelembe véve a körmembrán rezgésének problémáját (1738), a Bessel-egyenlethez jutott p = n egész számokkal, és megtalálta a J n (x) kifejezést sorozat formájában x hatványaiban; később ezt a kifejezést kiterjesztette a p tetszőleges értékeinek esetére. F. Bessel a bolygók Nap körüli mozgásának tanulmányozása kapcsán tanulmányozta (1824) a J p (x) függvényeket, és összeállította az első táblázatokat J 0 (x), J 1 (x) függvényekre.

Lit.: Watson G. N. Bessel-függvények elmélete. M., 1949. 1-2. rész; Lebedev N. N. Speciális funkciók és alkalmazásaik. 2. kiadás M.; L., 1963; Bateman G., Erdelyi A. Magasabb transzcendentális funkciók. Bessel-függvények, parabola hengerfüggvények, ortogonális polinomok. M., 1974.

A Bessel- vagy hengeres függvények a Bessel-féle lineáris differenciálegyenlet megoldásai

Ahol z- komplex változó, ν – paraméter, sorrend, ikon vagy index, tetszőleges komplex szám is lehet.

Az alkalmazásoknál gyakran figyelembe kell venni azt az esetet, amikor ν = n– egész szám. A következő függvények hengeres függvények: Bessel-függvények J ν (z), Neumann függvények N ν (z), gyakran Weber-függvényeknek nevezik a jelöléssel Y ν (z), és Hankel függvények H ν (1) (z), H ν (2) (z). A fixen elnevezett függvények
analitikus függvények z. Gyakran a Bessel-függvényeket kell figyelembe venni egy fixhez z mint ikon funkciók ν . Ráadásul ezek egy komplex változó teljes függvényei ν .

Egy teljes függvény egy analitikus függvény, amely egy mindenhol konvergens Taylor-sorral ábrázolható
.

Funkciók között J ν (z), N ν (z) vagy Y ν (z), H ν (1) (z), H ν (2) (z) vannak az Euler-képletekhez hasonló függőségek:

; .

Fizikai szempontból a harmonikus függvények állandó frekvenciájú csillapítatlan rezgéseket írnak le, míg a Bessel-függvények egy gyengén csillapított oszcillációs folyamatot, amelynek frekvenciája csak aszimptotikában válik állandóvá.

Megoldást keresünk a (6.13) egyenletre általánosított hatványsor formájában
, Ahol a mÉs a– a meghatározandó együtthatók és a paraméter értéke, két részmegoldást kapunk:

;
, (6.14)

amely at
lineárisan függetlenek, és lineáris kombinációjuk a (6.13) egyenlet általános megoldását képezi. Ha ν = n, majd a funkciók között J P (z) És J -P (z) az alaknak lineáris függése van
. Ahhoz, hogy általános megoldást kapjunk a (6.13) egyenletre ν = nés bevezetik a Neumann-függvényt. Funkciók J ν (z) És N ν (z) alapvető, lineárisan független megoldási rendszert alkotnak a Bessel-egyenlet bármely érték esetén v, beleértve az egész számokat is.

Egy tisztán képzeletbeli argumentum Bessel-függvényei (módosított Bessel-függvények). Ha azt feltételezzük
, Ahol x egy valós változó, akkor ezt az értéket (6.14) behelyettesítve kapjuk:

;
.

Az ezekben a kifejezésekben szereplő sorozatok határozzák meg a módosított Bessel-függvényeket

;
. (6.15)

Az a tény, hogy a (6.14) sorozatok előjelben váltakoznak, a (6.15) pedig állandó előjelűek, meghatározza viselkedésük éles különbségét (lásd a 6.9 és 6.10 ábrákat, amelyek a függvények grafikonjait mutatják J n (x) És én n (x) illetve).

A továbbiakban a Bessel-függvény argumentumát valós számnak tekintjük x. A Bessel-függvények megkülönböztetésének szabályát a következő ismétlődési reláció határozza meg:
. Főleg mikor
figyelembe véve azt a tényt
, kapunk:
.

Három szomszédos Bessel-függvény kapcsolódik a relációhoz

. (6.16)

Hasonló képletek érvényesek módosított Bessel-függvényekre:

;
.

A (6.15) definícióból, figyelembe véve a gammafüggvény viselkedését az argumentum negatív egész értékeire, könnyen kimutatható, hogy én  n (x) = én n (x) és ezért
.

Fél egész szám ikonnal
, Ahol n egy egész szám, a Bessel-függvényeket elemi függvényekkel fejezzük ki, mivel az összefüggések teljesülnek
És
, amely lehetővé teszi a (6.16) ismétlődési reláció használatát a meghatározására
, stb.

A fél egész számból álló ikonok Bessel-függvényeinek általános kifejezései a következő alakúak
És
, ahol a szimbólum
eszközök P- a mögötte lévő kifejezés többszörös differenciálása és az eredmény szorzása
minden megkülönböztetés után.

Az utólagos megkülönböztetés ennek a tényezőnek a figyelembevételével történik. Például,

A fenti kifejezések ismét hangsúlyozzák a Bessel-függvények viselkedésének oszcilláló és gyengén csillapított jellegét.

A Bessel-függvény aszimptotikus viselkedésének tanulmányozásakor az argumentum viselkedésének különböző forgatókönyveit veszik figyelembe. zés ikonra v. A legérdekesebb és legegyszerűbb eset az, amikor v rögzített és
. Ebben az esetben az első közelítés a
úgy néz ki, mint a

,

és ennek megfelelően,
.

A Bessel-függvények sajátossága, hogy a növekedéssel növekednek v rés
amelynél a Bessel-függvény nullához közelít.

A függvények generálása fontos szerepet játszik a Bessel-függvények tanulmányozásában. Így például ha kibővítjük a függvényt
komplex változó zés valódi t egy Laurent-sorozatba egy lényegében szinguláris pont szomszédságában z = 0, akkor kapunk
.

hinni
és a komplex számok egyenlőségének feltételeit felírva két fontos bővítést kapunk a gyakorlat számára:

honnan az következik

;
. (6.17)

Kihasználva azt a tényt
és figyelembe véve a koszinusz paritását és a szinusz páratlanságát, ezek a kifejezések a következő formában írhatók fel:

;
.

Ha ezekben a kifejezésekben helyettesítjük tovább
, akkor megkapjuk

;
.

Ezeket a bővítményeket Jacobiról nevezték el, aki először szerezte meg őket.

Az első egyenlőség (6.17) bal és jobb oldalát megszorozva ezzel
, a második pedig
és 0-tól integrálva , kapunk:

Ezeket az egyenlőségeket hozzáadva azt találjuk, hogy bármely P:

.

Ezt az integrált, amely a Bessel-függvény egész előjelű integrálábrázolásaként fogható fel, Bessel-integrálnak nevezzük. Nál nél n = 0 a Bessel-integrálból Parseval-integrál lesz:

.

Egyéni ikonhoz v tekintettel arra
A Poisson-képlet érvényes

.

Győződjön meg róla, hogy mikor v = 0 a Parseval integrált kapjuk, ezt önállóan javasoljuk az olvasónak.

Módosított Bessel-függvényekhez
nál nél
a Poisson-integrál reprezentációja érvényes

.

Nál nél v = 0 változó helyettesítéssel
integrál reprezentációt kaphat

.

Sok feladatban hasznosak a Bessel (hengeres) függvények összeadási tételei, amelyek közül a legegyszerűbb a következő.

Hadd
ábrán látható háromszög oldalai. 6.11, a És – az oldalakkal szemben fekvő szögei És hogy a koszinusz és szinusz tételeinek megfelelően
És
. Aztán azért
a forma bomlása van

,

Neumann-képletnek nevezett, ahol
- Neumann szimbólum.

Csere óta R  R, r 1  r 1 , r 2  r 2  és  szög nem változik, akkor a fenti képlet a következő formában írható fel:

.

Amikor  = j ezt figyelembe véve J k (x) = j k én k (x), k = 0, 1, 2, …, kapjuk:

.

Egyéni ikonhoz vösszeadási tételek J v (R) És én v (R) a következő formában jelenik meg:

,

.

A hengeres függvények nullái és a függvények kiterjesztése a Fourier-sorokban Bessel. Mint már említettük, az alap- vagy anyafüggvény nullái határozzák meg a léptéktényezőt a Bessel-függvényeken alapuló bázisrendszer felépítésénél. Tekintsük az egyenletet
. Ennek az egyenletnek a gyökereit a Bessel-függvény nulláinak nevezzük
és mint

A Bessel-függvények nullái
És
közbeiktatva. Kimutatható, hogy a függvényrendszer
, Ahol
–n az egyenlet gyöke
, ortogonális az intervallumra
súllyal x, azaz

Mivel az indexben szomszédos Bessel-függvények nullái átlapolva vannak, akkor
.

Ha a funkció f(x) darabonként folytonos és korlátozott változást mutat bármely intervallumban ( c, d), megfelel a 0. feltételnek< c < d < a, És

van egy integrál
, majd a Fourier–Bessel sorozat
, Ahol
, konvergál és van egy összege, azaz egybeesik vele
folytonosságának minden pontján.

Adjunk példát a Bessel-függvények használatára egy tipikus rádiótechnikai problémában.

Frekvenciamodulált (FM) rezgések spektruma harmonikus modulációs törvény mellett. Határozzuk meg annak a jelnek a spektrumát, amelynek pillanatnyi frekvenciája egyenlő, ahol
- frekvencia eltérés,
- vivőfrekvencia,
– modulációs frekvencia. Az oszcillációs fázis óta
, akkor esetünkben
. Hozzáállás
modulációs indexnek nevezzük. Amint az alábbiakból látni fogjuk, ez határozza meg az FM rezgések spektrumának szerkezetét a moduláció harmonikus törvénye szerint.. Egy tetszőleges állandó - a kezdeti fázis  nullára állítható az általánosság elvesztése nélkül. Így a vizsgált jel alakja a következő:

Ahol
– rezgés amplitúdója.

A jól ismert képlet segítségével a jelünket a formába írjuk

A (6.17) kiterjesztések és az említett trigonometrikus képlet alkalmazásával megkapjuk az FM rezgések spektrumának végső kifejezését harmonikus modulációs törvény mellett:

.

Így a vizsgált jel spektruma diszkrét jellegű, a harmonikusok amplitúdóit pedig a szám határozza meg. nés modulációs index. Figyelembe véve a Bessel-függvények viselkedésének oszcilláló jellegét, megjegyezzük, hogy amikor a modulációs index változik a harmonikusok amplitúdói közötti összefüggések megváltoznak.

ábrára hivatkozva. 6.9, könnyen belátható, hogy mikor
csak a függvények lesznek nullától eltérőek
,
És
; Hadd emlékeztessük erre
És
csak előjelben különböznek. Így mikor

Ha ehhez hozzávesszük, hogy mikor
feltételezhető
És
, akkor végül megkapjuk:

Meg kell jegyezni, hogy ugyanannak az amplitúdóspektrumnak van egy amplitúdómodulált oszcillációja, harmonikus modulációs törvényével. Kérjük az olvasót, hogy ellenőrizze ezt.

A modulációs index növekedésével a nullától eltérő harmonikusok száma nő, és az oszcillációs spektrum bővül. Mivel jó minőségű FM adás érhető el nagy modulációs indexekkel, világossá válik, hogy miért a VHF tartományban történik a jó minőségű sztereó adás, nem pedig a hosszú és közepes hullámokon.

Az űrlap Fredholm integrál operátora
, ahol a mag
Bessel-függvények vagy kapcsolódó függvények, meghatározza a Bessel-transzformációt. Ennek az átalakításnak az egyik leggyakrabban használt speciális esete a Hankel-transzformáció

, .

Az inverz operátor (inverziós képlet) alakja

.

A Bessel-transzformáció egyéb alkalmazási eseteivel ismerkedhet meg a segítségével.

Az első típusú Bessel-függvények, amelyeket jelöl, olyan megoldások, amelyek egész vagy nem negatív pontban végesek. Egy adott függvény kiválasztását és normalizálását annak tulajdonságai határozzák meg. Ezeket a függvényeket a Taylor-sor nulla körüli kiterjesztésével (vagy egy általánosabb hatványsorral a nem egész értékekhez) definiálhatjuk:

Itt van az Euler-féle gammafüggvény, a faktoriális értékek általánosítása nem egész számokra. A Bessel-függvény grafikonja hasonló egy szinuszoshoz, amelynek rezgései arányosan csillapodnak, bár valójában a függvény nullái nem periodikusan helyezkednek el.

Az alábbiakban a következő grafikonok láthatók:

Ha nem egész szám, a és függvények lineárisan függetlenek, ezért megoldásai az egyenletre. De ha ez egy egész szám, akkor a következő összefüggés igaz:

5. Periodikus jelek amplitúdó- és fázisspektrumának kiszámítása FFT eljárással;

Van egy fájl a mathcad-ben

A teljesítményspektrum megfelel az egyes frekvenciák amplitúdójának négyzeteként számított teljesítménynek, de nincs információja a kezdeti fázisról. Mivel a teljesítményspektrum elveszíti a kezdeti fázisinformációkat, megpróbálhatjuk az FFT-t használni a jel frekvenciájának és fázisinformációjának meghatározására.

Az FFT által biztosított kezdeti fázisinformáció a jel kezdőpontjához viszonyított fázis az időtartományban. Ezért a mintavételezést a jel valamely pontjáról el kell kezdeni, hogy konzisztens legyen

információk a kezdeti szakaszról. A szinusztörvény szerinti oszcilláció kezdeti fázisa -90°. A koszinusztörvény szerinti oszcilláció kezdeti fázisa 0°. Jellemzően a jelspektrum-analízis elsődleges célja a spektrumkomponensek közötti fáziskülönbség, vagy két egyidejűleg felvett harmonikus hullám közötti fáziskülönbség mérése. Néhány fejlett FFT funkció segítségével megtekintheti a két jel közötti fáziskülönbséget.

Ennek eredményeként az FFT kétoldalas spektrumot állít elő komplex formában valós és képzeletbeli részekkel. A jel minden harmonikus összetevőjének amplitúdójának és fázisának meghatározásához a kétirányú spektrumot skálázni és poláris formára kell konvertálni. A poláris alakzat frekvenciatengelye megegyezik a kétirányú teljesítményspektrum frekvenciatengelyével.

A DFT-t gyakran használják a jel spektrumának megfigyelésére és elemzésére.
Ebben az esetben gyakran csak az egyes harmonikusok Ck amplitúdói a legérdekesebbek, és nem a fázisaik. Ebben az esetben a spektrum általában az amplitúdó-frekvencia grafikonjaként jelenik meg (2. ábra). A frekvenciaskálát gyakran decibelben osztják. A decibelek nem magukat az amplitúdókat mérik, hanem azok arányait. Például a 20 dB eltérés 10-szeres amplitúdókülönbséget jelent, a 40 dB eltérés 100-szoros amplitúdókülönbséget jelent. A 2-szeres amplitúdókülönbség körülbelül 6 dB különbségnek felel meg. A decibel különbség kiszámításának képlete a következő:

A frekvenciaskálát is gyakran logaritmikus skálán osztják be.

A jel spektrumának kiszámítása előtt ki kell választania azt a jelszegmenst, amelyen a spektrum kiszámításra kerül. A szegmens hosszának kettős hatványnak kell lennie (az FFT működéséhez). Ellenkező esetben a jelet a kívánt hosszúságig nullákkal kell kitölteni. Ezt követően az FFT a jel kiválasztott részére kerül alkalmazásra. Esély

A spektrum ilyen módon történő kiszámításakor a következő nemkívánatos hatások lehetségesek. Amikor egy függvényt Fourier-sorrá bővítünk, feltételezzük, hogy a függvény periodikus, periódusa megegyezik az FFT méretével. Pont egy ilyen függvény spektrumát számítjuk ki (és nem azt, amelyből a darabot kivontuk). Ugyanakkor egy ilyen függvénynek bizonyosan lesznek megszakadásai a periódusok határain (elvégre az eredeti függvény nem volt periodikus). A funkció megszakításai pedig erősen befolyásolják a spektrumát, torzítva azt.

Ennek a hatásnak a kiküszöbölésére úgynevezett mérlegablakot használnak. Simán kiiktatják a funkciót az elemzett terület szélei közelében. A súlyablakok a Gauss-féle alakhoz hasonlóak. Az elemzésre kiválasztott jelszakaszt megszorozzuk egy súlyozási ablakkal, amely kiküszöböli a függvény folytonossági zavarait, amikor ez a jelszakasz „ciklusra kerül”. A virtuális hurok a DFT-ben történik, mivel a DFT algoritmus feltételezi, hogy a függvény periodikus. Számos mérlegablakot neveztek el alkotóikról. Mindegyik hasonló alakú, és nagymértékben kiküszöböli a figyelembe vett spektrumtorzulásokat. Két jó ablak képletét mutatjuk be: Hamming ablak és Blackman ablak (1. ábra):

Itt az ablakot alkalmazzuk a jelre 0-tól N-ig terjedő indexekkel. A Hamming-ablak a leggyakrabban használt. A Blackman ablak erősebb hatással van a figyelembe vett torzítások kiküszöbölésére, de vannak hátrányai.

Rizs. 1 Hamming (felső) és Blackman (alsó) mérőablak.

A spektrális analízis fontos tulajdonsága, hogy egyetlen jelnek sincs egyetlen, csak helyes spektruma. A spektrum különböző FFT-méretekkel és különböző súlyozási ablakokkal számítható ki. Előnyös, ha az egyes alkalmazásokhoz különböző módszereket alkalmazunk. A spektrum frekvenciája és időbeli felbontása az FFT méretétől függ. Ha a jelnek egy hosszú szakaszát választjuk ki spektrummá bontásra, jó frekvenciafelbontást kapunk, de gyenge időfelbontást (mivel a spektrum a jel átlagos viselkedését tükrözi a teljes FFT mintavételi szakaszon). Ha a jel egy rövid szakaszát választjuk ki spektrummá bontásra, pontosabb időbeni lokalizációt kapunk, de frekvenciában gyenge felbontást kapunk (mivel a Fourier-transzformációban túl kevés lesz az alapfrekvencia). A spektrumszámításnál ez a bizonytalansági kapcsolat alapelve: nem lehet egyszerre jó spektrumfelbontást elérni mind frekvenciában, mind időben: ezek a felbontások fordítottan arányosak.

A spektrális elemzés másik fontos tulajdonsága, hogy spektrumra bontva nem találjuk meg az eredeti jelet alkotó szinuszos komponenseket, hanem csak azt tudjuk meg, hogy bizonyos többszörös frekvenciákon milyen amplitúdókat kell felvennünk ahhoz, hogy az eredeti jelet megkapjuk. Más szóval, a dekompozíció nem az „eredeti jel frekvenciái”, hanem „az FFT algoritmus alapfrekvenciái” szerint történik. Ez azonban általában (főleg súlyozási ablakok használatakor) szinte észre sem vehető a spektrumgrafikonon, vagyis a spektrumgráf eléggé megfelelően tükrözi az eredeti jel frekvenciáit.

Rizs. 2. Különféle jelek töredékei (kb. 800 pont) és e jelek hosszabb szakaszainak spektruma (4096 pont). Felülről lefelé: zongora hangjegy, hang (ének), dob (rúgás), cintányér (nyitott hi-hat).

6. Impulzusjelek spektrális sűrűségének kiszámítása FFT segítségével