Penyelesaian persamaan derajat 5. Persamaan derajat yang lebih tinggi
Secara umum, persamaan derajat yang lebih besar dari 4 tidak dapat diselesaikan secara radikal. Namun terkadang kita masih dapat menemukan akar-akar polinomial di sebelah kiri dalam persamaan derajat tertinggi jika kita menyatakannya sebagai hasil kali polinomial dengan derajat tidak lebih dari 4. Penyelesaian persamaan tersebut didasarkan pada pemfaktoran polinomial, jadi kami menyarankan Anda untuk meninjau topik ini sebelum mempelajari artikel ini.
Paling sering Anda harus berurusan dengan persamaan derajat yang lebih tinggi dengan koefisien bilangan bulat. Dalam kasus ini, kita dapat mencoba mencari akar-akar rasional lalu memfaktorkan polinomialnya sehingga kita dapat mengubahnya menjadi persamaan derajat lebih rendah yang mudah diselesaikan. Dalam materi ini kita akan melihat contoh-contoh seperti itu.
Persamaan derajat yang lebih tinggi dengan koefisien bilangan bulat
Semua persamaan berbentuk a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 , kita dapat membuat persamaan berderajat sama dengan mengalikan kedua ruasnya dengan a n n - 1 dan mengubah bentuk variabel y = a n x:
an x n + an - 1 x n - 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n - 1 · a n n - 1 · x n - 1 + … + a 1 · (an) n - 1 · x + a 0 · (an) n - 1 = 0 y = an x ⇒ y n + b n - 1 y n - 1 + … + b 1 y + b 0 = 0
Koefisien yang dihasilkan juga akan berupa bilangan bulat. Jadi, kita perlu menyelesaikan persamaan tereduksi derajat ke-n dengan koefisien bilangan bulat, yang berbentuk x n + a n x n - 1 + ... + a 1 x + a 0 = 0.
Kami menghitung akar bilangan bulat persamaan. Jika persamaan memiliki akar bilangan bulat, Anda perlu mencarinya di antara pembagi suku bebas a 0 . Mari kita tuliskan dan substitusikan ke persamaan aslinya satu per satu, periksa hasilnya. Setelah kita memperoleh identitas dan menemukan salah satu akar persamaan, kita dapat menuliskannya dalam bentuk x - x 1 · P n - 1 (x) = 0. Di sini x 1 adalah akar persamaan, dan P n - 1 (x) adalah hasil bagi dari x n + a n x n - 1 + ... + a 1 x + a 0 dibagi x - x 1 .
Sisa pembagi yang dituliskan kita substitusikan ke dalam P n - 1 (x) = 0, dimulai dengan x 1, karena akar-akarnya dapat diulang. Setelah diperoleh identitasnya, akar x 2 dianggap ditemukan, dan persamaannya dapat dituliskan dalam bentuk (x - x 1) (x - x 2) · P n - 2 (x) = 0. Disini P n - 2 (x) adalah hasil bagi pembagian P n - 1 (x) dengan x - x 2.
Kami terus memilah-milah pembagi. Mari kita cari semua akar bilangan bulat dan nyatakan bilangannya sebagai m. Setelah itu, persamaan aslinya dapat direpresentasikan sebagai x - x 1 x - x 2 · … · x - x m · P n - m (x) = 0. Di sini P n - m (x) adalah polinomial dengan derajat n - m. Untuk perhitungannya lebih mudah menggunakan skema Horner.
Jika persamaan awal kita memiliki koefisien bilangan bulat, pada akhirnya kita tidak dapat memperoleh akar pecahan.
Kita mendapatkan persamaan P n - m (x) = 0, yang akar-akarnya dapat ditemukan dengan cara apa pun yang mudah. Mereka bisa jadi tidak rasional atau rumit.
Mari kita tunjukkan dengan contoh spesifik bagaimana skema solusi ini digunakan.
Contoh 1
Kondisi: tentukan penyelesaian persamaan x 4 + x 3 + 2 x 2 - x - 3 = 0.
Larutan
Mari kita mulai dengan mencari akar utuh.
Kami memiliki istilah bebas sama dengan minus tiga. Ia memiliki pembagi sama dengan 1, - 1, 3 dan - 3. Mari kita substitusikan keduanya ke dalam persamaan awal dan lihat persamaan mana yang memberikan identitas yang dihasilkan.
Jika x sama dengan satu, kita mendapatkan 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0, artinya satu akan menjadi akar persamaan ini.
Sekarang mari kita bagi polinomial x 4 + x 3 + 2 x 2 - x - 3 dengan (x - 1) dalam satu kolom:
Jadi x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.
1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0
Kita mendapat identitas, artinya kita menemukan akar persamaan lain yang sama dengan - 1.
Bagilah polinomial x 3 + 2 x 2 + 4 x + 3 dengan (x + 1) dalam sebuah kolom:
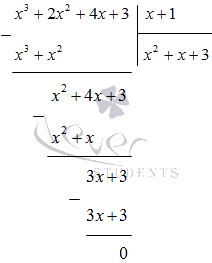
Kami mengerti
x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)
Kita substitusikan pembagi berikutnya ke dalam persamaan x 2 + x + 3 = 0, dimulai dari - 1:
1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0
Persamaan yang dihasilkan salah, artinya persamaan tersebut tidak lagi memiliki akar bilangan bulat.
Akar-akar yang tersisa akan menjadi akar-akar persamaan x 2 + x + 3.
D = 1 2 - 4 1 3 = - 11< 0
Oleh karena itu, trinomial kuadrat ini tidak mempunyai akar real, tetapi terdapat akar konjugat kompleks: x = - 1 2 ± i 11 2.
Mari kita perjelas bahwa alih-alih membagi menjadi sebuah kolom, skema Horner dapat digunakan. Hal ini dilakukan seperti ini: setelah kita menentukan akar pertama persamaan, kita mengisi tabelnya.
Pada tabel koefisien kita langsung dapat melihat koefisien hasil pembagian polinomial yang artinya x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3 .
Setelah menemukan root berikutnya, yaitu - 1, kita mendapatkan yang berikut:
Menjawab: x = - 1, x = 1, x = - 1 2 ± saya 11 2.
Contoh 2
Kondisi: selesaikan persamaan x 4 - x 3 - 5 x 2 + 12 = 0.
Larutan
Suku bebasnya mempunyai pembagi 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12.
Mari kita periksa secara berurutan:
1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0
Artinya x = 2 adalah akar persamaannya. Bagilah x 4 - x 3 - 5 x 2 + 12 dengan x - 2 menggunakan skema Horner:
Hasilnya, kita mendapatkan x - 2 (x 3 + x 2 - 3 x - 6) = 0.
2 3 + 2 2 - 3 2 - 6 = 0
Artinya 2 akan kembali menjadi root. Bagilah x 3 + x 2 - 3 x - 6 = 0 dengan x - 2:
Hasilnya, kita mendapatkan (x - 2) 2 · (x 2 + 3 x + 3) = 0.
Memeriksa pembagi yang tersisa tidak masuk akal, karena persamaan x 2 + 3 x + 3 = 0 lebih cepat dan mudah diselesaikan menggunakan diskriminan.
Mari selesaikan persamaan kuadrat:
x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0
Kita memperoleh pasangan akar konjugasi kompleks: x = - 3 2 ± i 3 2 .
Menjawab: x = - 3 2 ± saya 3 2 .
Contoh 3
Kondisi: Temukan akar real persamaan x 4 + 1 2 x 3 - 5 2 x - 3 = 0.
Larutan
x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0
Kita kalikan 2 3 pada kedua ruas persamaan:
2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0
Ganti variabel y = 2 x:
2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 tahun 4 + tahun 3 - 20 tahun - 48 = 0
Hasilnya, kami mendapatkan persamaan standar derajat ke-4, yang dapat diselesaikan sesuai skema standar. Mari kita periksa pembaginya, bagi dan dapatkan bahwa ia mempunyai 2 akar real y = - 2, y = 3 dan dua akar kompleks. Kami tidak akan memberikan solusi keseluruhan di sini. Karena substitusi tersebut, akar real persamaan ini adalah x = y 2 = - 2 2 = - 1 dan x = y 2 = 3 2.
Menjawab: x 1 = - 1 , x 2 = 3 2
Jika Anda melihat kesalahan pada teks, silakan sorot dan tekan Ctrl+Enter
Kunjungi saluran youtube situs web kami untuk terus mengikuti semua video pelajaran baru.
Pertama, mari kita ingat rumus dasar pangkat dan sifat-sifatnya.
Produk dari suatu angka A terjadi pada dirinya sendiri sebanyak n kali, kita dapat menulis ekspresi ini sebagai a a … a=an n
1. a 0 = 1 (a ≠ 0)
3. an am = an + m
4. (sebuah) m = sebuah nm
5. a n b n = (ab) n
7. an / am = an - m
Persamaan pangkat atau eksponensial– ini adalah persamaan yang variabelnya dipangkatkan (atau eksponen), dan basisnya adalah angka.
Contoh persamaan eksponensial:
Dalam contoh ini, angka 6 adalah basis; selalu di bawah, dan variabel X derajat atau indikator.
Mari kita berikan lebih banyak contoh persamaan eksponensial.
2 x *5=10
16 x - 4 x - 6=0
Sekarang mari kita lihat bagaimana persamaan eksponensial diselesaikan?
Mari kita ambil persamaan sederhana:
2 x = 2 3
Contoh ini dapat dipecahkan bahkan di kepala Anda. Dapat dilihat bahwa x=3. Lagi pula, agar ruas kiri dan kanan sama, Anda harus memasukkan angka 3, bukan x.
Sekarang mari kita lihat bagaimana memformalkan keputusan ini:
2 x = 2 3
x = 3
Untuk menyelesaikan persamaan seperti itu, kami menghilangkannya alasan yang identik(yaitu, dua) dan menuliskan sisanya, ini adalah derajat. Kami mendapat jawaban yang kami cari.
Sekarang mari kita rangkum keputusan kita.
Algoritma untuk menyelesaikan persamaan eksponensial:
1. Perlu diperiksa sama apakah persamaan tersebut mempunyai basis di kanan dan kiri. Jika alasannya tidak sama, kami mencari opsi untuk menyelesaikan contoh ini.
2. Setelah alasnya menjadi sama, menyamakan derajat dan selesaikan persamaan baru yang dihasilkan.
Sekarang mari kita lihat beberapa contoh:
Mari kita mulai dengan sesuatu yang sederhana.
Basis sisi kiri dan kanan sama dengan angka 2, artinya kita dapat membuang basisnya dan menyamakan pangkatnya.
x+2=4 Persamaan paling sederhana diperoleh.
x=4 – 2
x=2
Jawaban: x=2
Pada contoh berikut, Anda dapat melihat bahwa basisnya berbeda: 3 dan 9.
3 3x - 9 x+8 = 0
Pertama, pindahkan sembilan ke sisi kanan, kita mendapatkan:
Sekarang Anda perlu membuat pangkalan yang sama. Kita tahu bahwa 9=3 2. Mari kita gunakan rumus pangkat (an) m = a nm.
3 3x = (3 2) x+8
Kita peroleh 9 x+8 =(3 2) x+8 =3 2x+16
3 3x = 3 2x+16 Sekarang jelas bahwa sisi kiri dan kanan alasnya sama dan sama dengan tiga, artinya kita bisa membuangnya dan menyamakan derajatnya.
3x=2x+16 kita mendapatkan persamaan paling sederhana
3x - 2x=16
x=16
Jawaban: x=16.
Mari kita lihat contoh berikut:
2 2x+4 - 10 4 x = 2 4
Pertama-tama, kita melihat basisnya, basis dua dan empat. Dan kita membutuhkan mereka untuk menjadi sama. Kita transformasikan keempatnya menggunakan rumus (an) m = a nm.
4 x = (2 2) x = 2 2x
Dan kami juga menggunakan satu rumus a n a m = a n + m:
2 2x+4 = 2 2x 2 4
Tambahkan ke persamaan:
2 2x 2 4 - 10 2 2x = 24
Kami memberi contoh untuk alasan yang sama. Tapi angka 10 dan 24 lainnya mengganggu kita. Jika Anda perhatikan lebih dekat, Anda dapat melihat bahwa di sisi kiri kita memiliki 2 2x yang diulang, inilah jawabannya - kita dapat mengeluarkan 2 2x dari tanda kurung:
2 2x (2 4 - 10) = 24
Mari kita hitung ekspresi dalam tanda kurung:
2 4 — 10 = 16 — 10 = 6
Kami membagi seluruh persamaan dengan 6:
Bayangkan 4=2 2:
2 2x = 2 2 basanya sama, kita buang dan samakan derajatnya.
2x = 2 adalah persamaan paling sederhana. Bagilah dengan 2 dan kita dapatkan
x = 1
Jawaban: x = 1.
Mari selesaikan persamaannya:
9 x – 12*3 x +27= 0
Mari bertransformasi:
9 x = (3 2) x = 3 2x
Kami mendapatkan persamaan:
3 2x - 12 3 x +27 = 0
Basis kita sama, sama dengan tiga. Dalam contoh ini, Anda dapat melihat bahwa tiga bilangan pertama mempunyai derajat dua kali (2x) dibandingkan bilangan kedua (hanya x). Dalam hal ini, Anda bisa menyelesaikannya metode penggantian. Kita ganti angka tersebut dengan derajat terkecil:
Maka 3 2x = (3 x) 2 = t 2
Kami mengganti semua pangkat x dalam persamaan dengan t:
t 2 - 12t+27 = 0
Kami mendapatkan persamaan kuadrat. Menyelesaikan diskriminan, kita mendapatkan:
D=144-108=36
T 1 = 9
t2 = 3
Kembali ke variabel X.
Ambil t 1:
t 1 = 9 = 3 x
Itu adalah,
3x = 9
3 x = 3 2
x 1 = 2
Satu akar ditemukan. Kami mencari yang kedua dari t 2:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Jawaban: x 1 = 2; x 2 = 1.
Di situs web Anda dapat mengajukan pertanyaan apa pun yang Anda miliki di bagian BANTUAN MEMUTUSKAN, kami pasti akan menjawab Anda.
Bergabunglah dengan grup
Mari kita pertimbangkan menyelesaikan persamaan dengan satu variabel yang derajatnya lebih tinggi dari variabel kedua.
Derajat persamaan P(x) = 0 adalah derajat polinomial P(x), yaitu pangkat terbesar dari suku-sukunya dengan koefisien tidak sama dengan nol.
Jadi, misalnya persamaan (x 3 – 1) 2 + x 5 = x 6 – 2 mempunyai derajat kelima, karena setelah operasi pembukaan tanda kurung dan pengurangan tanda kurung, diperoleh persamaan ekuivalen x 5 – 2x 3 + 3 = 0 derajat kelima.
Mari kita mengingat kembali aturan-aturan yang diperlukan untuk menyelesaikan persamaan derajat yang lebih tinggi dari dua.
Pernyataan tentang akar-akar polinomial dan pembaginya:
1. Polinomial derajat ke-n mempunyai jumlah akar tidak melebihi n, dan akar-akar multiplisitas m muncul tepat m kali.
2. Polinomial berderajat ganjil mempunyai paling sedikit satu akar real.
3. Jika α adalah akar dari P(x), maka P n (x) = (x – α) · Q n – 1 (x), dimana Q n – 1 (x) adalah polinomial berderajat (n – 1) .
4.
5. Polinomial tereduksi dengan koefisien bilangan bulat tidak boleh memiliki akar rasional pecahan.
6. Untuk polinomial derajat ketiga
P 3 (x) = ax 3 + bx 2 + cx + d salah satu dari dua hal yang mungkin: dapat didekomposisi menjadi produk tiga binomial
Р 3 (x) = а(х – α)(х – β)(х – γ), atau didekomposisi menjadi hasil kali binomial dan trinomial persegi Р 3 (x) = а(х – α)(х 2 + βх + γ ).
7. Polinomial derajat keempat apa pun dapat diekspansi menjadi hasil kali dua trinomial persegi.
8. Suatu polinomial f(x) habis dibagi oleh suatu polinomial g(x) tanpa sisa jika terdapat polinomial q(x) sehingga f(x) = g(x) · q(x). Untuk membagi polinomial, digunakan aturan “pembagian sudut”.
9. Agar polinomial P(x) habis dibagi binomial (x – c), bilangan c harus menjadi akar dari P(x) (akibat teorema Bezout).
10. Teorema Vieta: Jika x 1, x 2, ..., x n adalah akar real dari polinomial
P(x) = a 0 x n + a 1 x n - 1 + ... + a n, maka persamaan berikut berlaku:
x 1 + x 2 + … + x n = -a 1 /a 0,
x 1 x 2 + x 1 x 3 + … + x n – 1 x n = a 2 /a 0,
x 1 x 2 x 3 + … + x n – 2 x n – 1 x n = -a 3 / a 0,
x 1 · x 2 · x 3 · x n = (-1) n a n / a 0 .
Contoh Penyelesaian
Contoh 1.
Hitunglah sisa pembagian P(x) = x 3 + 2/3 x 2 – 1/9 dengan (x – 1/3).
Larutan.
Akibat wajar dari teorema Bezout: “Sisa polinomial dibagi binomial (x – c) sama dengan nilai polinomial c.” Mari kita cari P(1/3) = 0. Jadi, sisanya adalah 0 dan bilangan 1/3 adalah akar polinomialnya.
Jawaban: R = 0.
Contoh 2.
Bagilah dengan “sudut” 2x 3 + 3x 2 – 2x + 3 dengan (x + 2). Temukan sisa dan hasil bagi tidak lengkap. 
Larutan:
2x 3 + 3x 2 – 2x + 3| x + 2
2x 3 + 4x 2 2x 2 – x
x 2 – 2 x
Jawaban: R = 3; hasil bagi: 2x 2 – x.
Metode dasar untuk menyelesaikan persamaan derajat yang lebih tinggi
1. Pengenalan variabel baru
Cara memasukkan variabel baru sudah familiar dari contoh persamaan biquadratic. Terdiri dari kenyataan bahwa untuk menyelesaikan persamaan f(x) = 0, variabel baru (substitusi) t = x n atau t = g(x) dimasukkan dan f(x) dinyatakan melalui t, memperoleh persamaan baru r (T). Kemudian menyelesaikan persamaan r(t), akar-akarnya ditemukan:
(t 1, t 2, …, t n). Setelah ini, diperoleh himpunan n persamaan q(x) = t 1 , q(x) = t 2 , … , q(x) = t n, yang darinya diperoleh akar-akar persamaan aslinya.
Contoh 1.
(x 2 + x + 1) 2 – 3x 2 – 3x – 1 = 0.
Larutan:
(x 2 + x + 1) 2 – 3(x 2 + x) – 1 = 0.
(x 2 + x + 1) 2 – 3(x 2 + x + 1) + 3 – 1 = 0.
Substitusi (x 2 + x + 1) = t.
t 2 – 3t + 2 = 0.
t 1 = 2, t 2 = 1. Substitusi terbalik:
x 2 + x + 1 = 2 atau x 2 + x + 1 = 1;
x 2 + x - 1 = 0 atau x 2 + x = 0;
Jawaban: Dari persamaan pertama: x 1, 2 = (-1 ± √5)/2, dari persamaan kedua: 0 dan -1.
2. Faktorisasi dengan mengelompokkan dan menyingkat rumus perkalian
Dasar dari metode ini juga bukanlah hal baru dan terdiri dari pengelompokan suku-suku sedemikian rupa sehingga setiap kelompok mengandung faktor yang sama. Untuk melakukan ini, terkadang perlu menggunakan beberapa teknik buatan.
Contoh 1.
x 4 – 3x 2 + 4x – 3 = 0.
Larutan.
Bayangkan - 3x 2 = -2x 2 – x 2 dan kelompokkan:
(x 4 – 2x 2) – (x 2 – 4x + 3) = 0.
(x 4 – 2x 2 +1 – 1) – (x 2 – 4x + 3 + 1 – 1) = 0.
(x 2 – 1) 2 – 1 – (x – 2) 2 + 1 = 0.
(x 2 – 1) 2 – (x – 2) 2 = 0.
(x 2 – 1 – x + 2)(x 2 – 1 + x - 2) = 0.
(x 2 – x + 1)(x 2 + x – 3) = 0.
x 2 – x + 1 = 0 atau x 2 + x – 3 = 0.
Jawab: Persamaan pertama tidak mempunyai akar, dari persamaan kedua: x 1, 2 = (-1 ± √13)/2.
3. Faktorisasi dengan metode koefisien tak tentu
Inti dari metode ini adalah polinomial asli difaktorkan dengan koefisien yang tidak diketahui. Dengan menggunakan sifat polinomial yang sama jika koefisiennya sama untuk pangkat yang sama, koefisien muai yang tidak diketahui ditemukan.
Contoh 1.
x 3 + 4x 2 + 5x + 2 = 0.
Larutan.
Polinomial berderajat 3 dapat diekspansi menjadi hasil kali faktor linier dan kuadrat.
x 3 + 4x 2 + 5x + 2 = (x – a)(x 2 + bx + c),
x 3 + 4x 2 + 5x + 2 = x 3 +bx 2 + cх – kapak 2 – abх – ac,
x 3 + 4x 2 + 5x + 2 = x 3 + (b – a)x 2 + (cx – ab)x – ac.
Setelah memecahkan sistem:
(b – a = 4,
(c – ab = 5,
(-ac = 2,
(sebuah = -1,
(b = 3,
(c = 2, yaitu
x 3 + 4x 2 + 5x + 2 = (x + 1)(x 2 + 3x + 2).
Akar-akar persamaan (x + 1)(x 2 + 3x + 2) = 0 mudah ditemukan.
Jawaban 1; -2.
4. Cara pemilihan akar menggunakan koefisien tertinggi dan bebas

Metode ini didasarkan pada penerapan teorema:
1) Setiap akar bilangan bulat dari suatu polinomial dengan koefisien bilangan bulat adalah pembagi suku bebasnya.
2) Agar pecahan tak tersederhanakan p/q (p adalah bilangan bulat, q adalah bilangan asli) menjadi akar persamaan dengan koefisien bilangan bulat, bilangan p harus merupakan pembagi bilangan bulat dari suku bebas a 0, dan q adalah pembagi natural dari koefisien terdepan.
Contoh 1.
6x 3 + 7x 2 – 9x + 2 = 0.
Larutan:
6: q = 1, 2, 3, 6.
Oleh karena itu, p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.
Setelah menemukan satu akar, misalnya – 2, kita akan mencari akar lainnya menggunakan pembagian sudut, metode koefisien tak tentu, atau skema Horner.
Jawaban: -2; 1/2; 1/3.
Masih ada pertanyaan? Tidak tahu cara menyelesaikan persamaan?
Untuk mendapatkan bantuan dari tutor, daftarlah.
Pelajaran pertama gratis!
situs web, ketika menyalin materi secara keseluruhan atau sebagian, diperlukan tautan ke sumber aslinya.
Pada abad ke-16, para ahli matematika menemukan bilangan kompleks secara tidak sengaja (lihat Bab 11). Pada abad ke-18, bilangan kompleks dianggap sebagai perpanjangan bidang bilangan real, namun penggunaan bilangan kompleks masih menimbulkan kesalahan paritas, karena karya besar Leonard E. tentang teori bilangan, Arithmetical Investigations (1801), menghindari penggunaan bilangan kompleks. yang disebut "bilangan imajiner". Bagi saya, bagian terpenting dari karya ini adalah bukti pertama dari teorema dasar aljabar. Gauss menyadari betapa pentingnya teorema ini, menghasilkan beberapa bukti tambahan pada tahun-tahun berikutnya. Pada tahun 1849, ia mengerjakan ulang versi pertama, kali ini menggunakan bilangan kompleks. Dalam istilah modern, kita dapat mengatakan bahwa untuk setiap persamaan polinomial berhingga dengan koefisien real atau kompleks, semua akarnya adalah bilangan real atau kompleks. Dengan demikian, kita mendapatkan jawaban negatif terhadap pertanyaan lama apakah menyelesaikan persamaan polinomial orde tinggi memerlukan pembangkitan bilangan dengan orde lebih tinggi daripada bilangan kompleks.
Salah satu masalah paling pelik dalam aljabar pada masa itu adalah pertanyaan apakah polinomial orde kelima, kuintik, dapat diselesaikan dengan metode aljabar, yaitu menggunakan sejumlah langkah aljabar yang terbatas. Saat ini di sekolah mereka mengajarkan rumus untuk menyelesaikan persamaan kuadrat, dan sejak abad ke-16 telah dikenal metode serupa untuk menyelesaikan persamaan derajat ketiga dan keempat (Bab 11). Namun tidak ada satu pun metode yang ditemukan untuk quintics. Teorema dasar aljabar mungkin tampak memiliki prospek jawaban positif, namun pada kenyataannya teorema tersebut hanya menjamin bahwa solusi ada, tidak menjelaskan apa pun tentang keberadaan rumus yang memberikan solusi eksak (perkiraan metode numerik dan grafis sudah ada pada saat itu). ). Dan kemudian dua orang jenius matematika dengan nasib tragis muncul.
Niels Henrik Abel (1802–1829) dilahirkan dalam keluarga besar miskin yang tinggal di sebuah desa kecil di Norwegia, sebuah negara yang hancur akibat perang bertahun-tahun dengan Inggris dan Swedia. Gurunya, yang baik hati kepada anak laki-laki itu, memberinya pelajaran privat, tetapi setelah kematian ayahnya, pada usia delapan belas tahun, meskipun usianya masih muda dan kesehatannya lemah, Abel terpaksa menghidupi keluarganya. Pada tahun 1824, ia menerbitkan sebuah artikel ilmiah yang menyatakan bahwa kuintik tidak dapat diselesaikan dengan cara aljabar, seperti halnya polinomial tingkat tinggi lainnya. Abel percaya bahwa artikel ini akan menjadi tiketnya ke dunia ilmiah, dan mengirimkannya ke Gauss di Universitas Göttingen. Sayangnya, Gauss tidak pernah sempat memotong halaman dengan pisau (setiap pembaca harus melakukan ini pada masa itu) dan tidak membaca artikelnya. Pada tahun 1826, pemerintah Norwegia akhirnya menyediakan dana bagi Abel untuk berkeliling Eropa. Khawatir komunikasi pribadi dengan Gauss tidak akan memberinya banyak kegembiraan, ahli matematika tersebut memutuskan untuk tidak mengunjungi Göttingen dan malah pergi ke Berlin. Di sana ia berteman dengan August Leopold Krelle (1780–1855), seorang matematikawan, arsitek dan insinyur yang menjadi penasihat Kementerian Pendidikan Prusia dalam bidang matematika. Krell bermaksud mendirikan Jurnal Matematika Murni dan Terapan. Sehingga Abel mendapat kesempatan untuk mendiseminasikan karyanya dan banyak menerbitkannya, terutama pada edisi-edisi awal Jurnal yang segera dianggap sebagai publikasi ilmiah yang sangat bergengsi dan berwibawa. Orang Norwegia itu menerbitkan versi panjang buktinya bahwa kuintik tidak dapat ditentukan dengan metode aljabar. Dan kemudian dia berangkat ke Paris. Perjalanan ini sangat mengecewakan Abel, karena dia praktis tidak menerima dukungan yang dia butuhkan dari ahli matematika Perancis. Ia menjadi dekat dengan Augustin Louis Cauchy (1789–1857), yang merupakan tokoh analisis matematika terkemuka pada saat itu, namun memiliki karakter yang sangat kompleks. Seperti yang dikatakan Abel sendiri, "Cauchy gila dan tidak ada yang bisa dilakukan untuk mengatasinya, meskipun saat ini dia adalah satu-satunya yang mampu melakukan apa pun dalam matematika." Jika kita mencoba membenarkan manifestasi rasa tidak hormat dan pengabaian yang berasal dari Gauss dan Cauchy, kita dapat mengatakan bahwa quintic mencapai ketenaran tertentu dan menarik perhatian baik ahli matematika maupun orisinalis yang dihormati. Abel kembali ke Norwegia, di mana ia semakin menderita TBC. Dia terus mengirimkan karyanya ke Crelle, tetapi meninggal pada tahun 1829, tidak menyadari betapa reputasinya telah mapan di dunia ilmiah. Dua hari setelah kematiannya, Abel menerima tawaran untuk mengambil posisi ilmiah di Berlin.
Abel menunjukkan bahwa polinomial apa pun di atas orde keempat tidak dapat diselesaikan dengan menggunakan akar kuadrat, akar pangkat tiga, atau akar pangkat lebih tinggi. Namun, kondisi eksplisit di mana, dalam kasus khusus, polinomial ini dapat diselesaikan, dan metode penyelesaiannya, dirumuskan oleh Galois. Évariste Galois (1811–1832) menjalani kehidupan yang singkat dan penuh peristiwa. Dia adalah seorang ahli matematika yang sangat berbakat. Galois tidak kenal ampun terhadap orang-orang yang dianggapnya kurang berbakat dibandingkan dirinya, dan pada saat yang sama ia membenci ketidakadilan sosial. Dia tidak menunjukkan bakat matematika sampai dia membaca Elements of Geometry karya Legendre (diterbitkan pada tahun 1794, buku ini menjadi buku teks utama selama seratus tahun berikutnya). Kemudian dia benar-benar melahap sisa karya Legendre dan, kemudian, Abel. Antusiasme, kepercayaan diri, dan intoleransinya menimbulkan konsekuensi yang sangat buruk dalam hubungannya dengan guru dan penguji. Galois mengikuti kompetisi untuk masuk ke Ecole Polytechnique, tempat lahirnya matematika Perancis, namun gagal dalam ujian karena kurangnya persiapan. Untuk beberapa waktu setelah bertemu dengan guru baru yang mengenali bakatnya, dia berhasil mengendalikan emosinya. Pada bulan Maret 1829, Galois menerbitkan makalah pertamanya tentang pecahan lanjutan, yang dianggapnya sebagai karyanya yang paling signifikan. Dia mengirim pesan tentang penemuannya ke Akademi Ilmu Pengetahuan, dan Cauchy berjanji untuk mempresentasikannya, tapi lupa. Apalagi dia kehilangan naskahnya begitu saja.
Kegagalan kedua Galois untuk masuk ke École Polytechnique telah menjadi bagian dari cerita rakyat matematika. Dia begitu terbiasa terus-menerus menyimpan ide-ide matematika yang rumit di kepalanya sehingga dia marah karena omelan kecil dari para penguji. Karena penguji kesulitan memahami penjelasannya, dia melemparkan penghapus papan tulis ke wajah salah satu dari mereka. Segera setelah itu, ayahnya meninggal karena bunuh diri akibat intrik gereja. Kerusuhan praktis terjadi di pemakamannya. Pada bulan Februari 1830, Galois menulis tiga makalah berikut, mengirimkannya ke Akademi Ilmu Pengetahuan untuk Grand Prix Matematika. Joseph Fourier, yang saat itu menjadi sekretaris akademi, meninggal tanpa membacanya, dan setelah kematiannya, artikel-artikel tersebut tidak ditemukan di antara makalahnya. Gelombang kekecewaan seperti itu akan membuat siapa pun kewalahan. Galois memberontak melawan penguasa karena dia merasa mereka tidak mengakui jasanya dan menghancurkan ayahnya. Dia terjun langsung ke dunia politik, menjadi seorang republikan yang bersemangat - bukan keputusan paling bijaksana di Prancis pada tahun 1830. Dalam upaya terakhirnya, ia mengirimkan makalah ilmiah kepada fisikawan dan matematikawan Prancis terkenal Simeon Denis Poisson (1781–1840), yang menanggapinya dengan meminta bukti lebih lanjut.
Ini adalah pukulan terakhir. Pada tahun 1831, Galois ditangkap dua kali - pertama karena diduga menyerukan pembunuhan Raja Louis Philippe, dan kemudian untuk melindunginya - pihak berwenang takut akan pemberontakan republik! Kali ini dia dijatuhi hukuman enam bulan penjara atas tuduhan palsu mengenakan seragam batalion artileri yang dibubarkan di mana dia bergabung secara ilegal. Dibebaskan dengan pembebasan bersyarat, dia mengambil tugas yang membuatnya jijik seperti semua hal lain dalam hidup. Dalam suratnya kepada sahabat setianya Chevalier, kekecewaannya sangat terasa. Pada tanggal 29 Mei 1832, ia menerima tantangan duel, yang alasannya tidak sepenuhnya dipahami. “Saya menjadi korban genit yang tidak jujur. Hidup saya sedang sekarat dalam pertengkaran yang menyedihkan,” tulisnya dalam “Surat untuk Semua Partai Republik.” Karya Galois yang paling terkenal dibuat sketsanya pada malam sebelum duel fatal tersebut. Di pinggirannya tersebar keluhan-keluhan: “Saya tidak punya waktu lagi, saya tidak punya waktu lagi.” Dia terpaksa menyerahkan kepada orang lain penjelasan rinci tentang langkah-langkah peralihan yang tidak penting untuk memahami gagasan utama. Dia perlu menuliskan di atas kertas dasar penemuannya - asal mula dari apa yang sekarang disebut teorema Galois. Dia mengakhiri wasiatnya dengan meminta Chevalier untuk "meminta Jacobi dan Gauss untuk memberikan opini publik mereka, bukan mengenai kebenarannya, tetapi mengenai pentingnya teorema ini." Pagi-pagi sekali, Galois pergi menemui saingannya. Mereka harus menembak dari jarak 25 langkah. Galois terluka dan meninggal di rumah sakit keesokan paginya. Dia baru berusia dua puluh tahun.
Galois mengembangkan karya Lagrange dan Cauchy, namun ia mengembangkan metode yang lebih umum. Ini merupakan pencapaian yang sangat penting dalam bidang penyelesaian quintics. Ilmuwan kurang memperhatikan persamaan asli atau interpretasi grafis, dan lebih memikirkan sifat akar itu sendiri. Untuk menyederhanakannya, Galois hanya mempertimbangkan apa yang disebut kuintik tak tersederhanakan, yaitu kuintik yang tidak dapat difaktorkan dalam bentuk polinomial berorde lebih rendah (seperti yang telah kami katakan, untuk setiap persamaan polinomial hingga orde keempat, terdapat rumus untuk mencarinya akar). Secara umum, polinomial tak tereduksi dengan koefisien rasional adalah polinomial yang tidak dapat diuraikan menjadi polinomial sederhana yang memiliki koefisien rasional. Misalnya, (x 5 - 1) dapat difaktorkan (x-1)(x 4 + x 3 + x 2 + x + 1), sedangkan (x 5 - 2) Tidak dapat direduksi. Tujuan Galois adalah untuk menentukan kondisi di mana semua solusi persamaan polinomial umum yang tidak dapat direduksi dapat ditemukan dalam bentuk radikal.
Kunci dari penyelesaiannya adalah bahwa akar-akar persamaan aljabar tak tereduksi tidak berdiri sendiri, akar-akar tersebut dapat dinyatakan melalui persamaan aljabar lainnya. Hubungan-hubungan ini diformalkan ke dalam kelompok semua kemungkinan permutasi, yang disebut kelompok simetri akar - untuk kuintik, kelompok ini berisi 5! = 5 x 4 x 3 x 2 x 1 = 120 elemen. Algoritme matematika teori Galois sangat kompleks, dan kemungkinan besar, sebagian karena hal ini, pada awalnya sulit untuk dipahami. Namun begitu tingkat abstraksi memungkinkannya beralih dari solusi aljabar persamaan ke struktur aljabar kelompok terkait, Galois mampu memprediksi solvabilitas suatu persamaan berdasarkan sifat-sifat kelompok tersebut. Selain itu, teorinya juga memberikan metode yang dapat digunakan untuk menemukan akar-akar ini. Sedangkan mengenai kuintik, ahli matematika Joseph Liouville (1809–1882), yang pada tahun 1846 menerbitkan sebagian besar karya Galois dalam Journal of Pure and Applied Mathematics, mencatat bahwa ilmuwan muda tersebut telah membuktikan “teorema yang indah”, dan dalam rangka “untuk Jika persamaan tak tersederhanakan dengan derajat awal dapat diselesaikan dalam bentuk radikal, semua akar persamaan tersebut perlu dan cukup merupakan fungsi rasional dari dua persamaan tersebut.” Karena hal ini tidak mungkin dilakukan oleh quintic, maka hal ini tidak dapat diselesaikan dengan menggunakan radikal.
Dalam tiga tahun, dunia matematika telah kehilangan dua bintang barunya yang paling terang. Saling tuduh dan pencarian jiwa pun terjadi, dan Abel serta Galois mendapatkan pengakuan yang memang layak mereka dapatkan, namun hanya secara anumerta. Pada tahun 1829, Carl Jacobi, melalui Legendre, mengetahui manuskrip Abel yang "hilang", dan pada tahun 1830 skandal diplomatik meletus ketika konsul Norwegia di Paris menuntut agar artikel rekan senegaranya ditemukan. Cauchy akhirnya menemukan artikel itu, namun artikel itu hilang lagi oleh editor akademi! Pada tahun yang sama, Abel dianugerahi Grand Prix Matematika (bersama dengan Jacobi) - tapi dia sudah meninggal. Pada tahun 1841, biografinya diterbitkan. Pada tahun 1846, Liouville mengedit beberapa manuskrip Galois untuk diterbitkan dan dalam pendahuluan menyatakan penyesalannya bahwa akademi awalnya menolak karya Galois karena kerumitannya - "kejelasan presentasi memang diperlukan ketika penulis membawa pembaca keluar dari jalur yang sulit menuju alam liar yang belum dipetakan. wilayah." Dia melanjutkan: “Galois sudah tidak ada lagi! Janganlah kita terjerumus ke dalam kritik yang tidak berguna. Mari kita kesampingkan kekurangannya dan lihat kelebihannya!” Buah dari kehidupan singkat Galois hanya muat dalam enam puluh halaman. Editor jurnal matematika untuk calon École Normale dan École Polytechnique mengomentari kasus Galois sebagai berikut: “Seorang kandidat yang memiliki kecerdasan tinggi dieliminasi oleh penguji dengan tingkat pemikiran yang lebih rendah. Barbarus hic ego sum, quia non intelligor illis."
Pertama-tama, halaman kedua karya ini tidak dibebani dengan nama, nama keluarga, deskripsi status sosial, gelar dan keanggunan untuk menghormati beberapa pangeran pelit, yang dompetnya akan dibuka dengan bantuan dupa ini - dengan ancaman penutupan itu ketika pujian berakhir. Anda tidak akan melihat di sini pidato-pidato yang penuh hormat, ditulis dengan huruf tiga kali lebih besar dari teks itu sendiri, ditujukan kepada mereka yang memiliki kedudukan tinggi dalam sains, kepada pelindung yang bijaksana - sesuatu yang wajib (menurut saya tidak dapat dihindari) bagi seseorang pada usia dua puluh yang ingin untuk menulis sesuatu. Saya tidak mengatakan kepada siapa pun di sini bahwa saya berhutang nasihat dan dukungan mereka atas semua kebaikan yang dihasilkan dari pekerjaan saya. Saya tidak mengatakan ini karena itu bohong. Jika saya menyebut salah satu orang terhebat dalam masyarakat atau ilmu pengetahuan (perbedaan antara kedua kelompok masyarakat ini hampir tidak terlihat pada saat ini), saya bersumpah itu bukanlah tanda terima kasih. Saya berhutang budi kepada mereka karena saya terlambat menerbitkan artikel pertama dari dua artikel ini, dan saya menulis semua ini di penjara - tempat yang sulit dianggap cocok untuk refleksi ilmiah, dan saya sering kagum dengan pengekangan dan kemampuan saya untuk menjaga diri saya sendiri. mulutku tertutup. kastil sehubungan dengan zoile yang bodoh dan jahat. Saya rasa saya bisa menggunakan kata "zoiles" tanpa takut dituduh tidak pantas, karena itulah yang saya sebut sebagai lawan saya. Saya tidak akan menulis di sini tentang bagaimana dan mengapa saya dikirim ke penjara, tetapi saya harus mengatakan bahwa naskah saya lebih sering hilang begitu saja di arsip tuan-tuan anggota akademi, meskipun, sebenarnya, saya tidak dapat membayangkan hal seperti itu. kecerobohan pihak orang yang bertanggung jawab atas kematian Habel. Menurut saya, siapa pun ingin dibandingkan dengan ahli matematika brilian ini. Cukuplah untuk mengatakan bahwa artikel saya tentang teori persamaan dikirim ke Akademi Ilmu Pengetahuan pada bulan Februari 1830, bahwa kutipan dari artikel tersebut dikirim pada bulan Februari 1829, tetapi tidak ada satupun yang dicetak, dan bahkan manuskripnya ternyata tidak mungkin. kembali.
Galois, kata pengantar yang tidak diterbitkan, 1832










