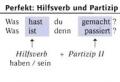
Sonlar qatorining yaqinlashuv belgilari. Raqamli qatorlar: ta’riflar, xossalar, yaqinlashish belgilari, misollar, yechimlar Qatorlarning yaqinlashuv mezonlari

Ta'rif 1.1. Umumiy atamaga ega bo'lgan raqamlar qatori qo'shish belgisi bilan bog'langan raqamlar ketma-ketligi, ya'ni shaklning ifodasidir:

Bu qatorni shaklda ham yozish mumkin

1.1-misol. Agar seriya quyidagicha ko'rinadi:

Ba'zan seriya yozishda uning faqat bir necha birinchi a'zolari yoziladi. Bu ketma-ketlik a'zolarining namunaviy xarakteristikasi osongina aniqlanganda amalga oshiriladi. Qat'iy aytganda, qatorni ko'rsatishning bu usuli matematik jihatdan to'g'ri emas, chunki ketma-ketlikning birinchi bir necha hadlaridan umumiy atama uchun formulani olish yagona yechimga ega bo'lmagan muammodir.

1.2-misol. Keling, seriyaning umumiy hadi uchun mumkin bo'lgan formulalardan birini yozamiz, uning dastlabki 4 ta shartini bilib olamiz:

Yechim. Avval 2, 5, 8, 11 sonlar ketma-ketligini ko‘rib chiqamiz. Ular arifmetik progressiya hosil qiladi, birinchi hadi 2, farqi esa 3. Bu arifmetikaning umumiy hadi formulasini olish imkonini beradi. progressiya hisoblagichning umumiy ifodasi sifatida: 2, 6, 18, 54 maxrajlar bilan geometrik progressiya hosil qiladi.

birinchi hadi 2, maxraji 3. Ularning umumiy ifodasi sifatida geometrik progressiyaning umumiy hadi formulasini olishimiz mumkin.Demak, qatorning umumiy hadi quyidagi ko rinishga ega bo ladi.

Shuni ta'kidlash kerakki, murakkabroq ibora umumiy atama sifatida qabul qilinishi mumkin

KIRISH

Uslubiy qo‘llanma texnikumlarning matematika fani o‘qituvchilari hamda barcha mutaxassisliklarning 2-kurs talabalari uchun mo‘ljallangan.

Ushbu maqola seriyalar nazariyasining asosiy tushunchalarini tavsiflaydi. Nazariy material o'rta kasb-hunar ta'limining Davlat ta'lim standarti talablariga javob beradi (Rossiya Federatsiyasi Ta'lim vazirligi. M., 2002).

Butun mavzu bo'yicha nazariy material taqdimoti ko'plab misollar va muammolarni ko'rib chiqish bilan birga keladi va imkon qadar qat'iy tilda olib boriladi. Qo'llanma oxirida talabalar o'z-o'zini nazorat qilish rejimida bajarishi mumkin bo'lgan misollar va topshiriqlar mavjud.

Qo‘llanma sirtqi va kunduzgi bo‘lim talabalari uchun mo‘ljallangan.

Texnik maktab o'quvchilarining tayyorgarlik darajasini, shuningdek, texnik maktablarda oliy matematikadan o'tish uchun dastur tomonidan ajratilgan juda cheklangan soatlar sonini (12 soat + 4 funt) hisobga olgan holda, o'zlashtirish uchun katta qiyinchiliklar tug'diradigan qat'iy xulosalar. , tashlab qo'yilgan, misollarni ko'rib chiqish bilan cheklanamiz.

ASOSIY TUSHUNCHALAR

Matematik nuqtai nazardan, masalan, turli funktsiyalar, ularning hosilalari va integrallarining kombinatsiyasi ko'rinishida taqdim etilgan muammoning echimi uni "songa etkazish" imkoniyatiga ega bo'lishi kerak, bu ko'pincha yakuniy javob bo'lib xizmat qiladi. Shu maqsadda matematikaning turli sohalarida turli usullar ishlab chiqilgan.

Matematikaning har qanday yaxshi qo‘yilgan masalani amaliy foydalanish uchun yetarli darajada aniqlik bilan yechish imkonini beruvchi bo‘limi qatorlar nazariyasi deb ataladi.

Matematik analizning ba'zi nozik tushunchalari qatorlar nazariyasi bilan bog'liq bo'lmagan holda paydo bo'lgan taqdirda ham, ular darhol qatorlarga qo'llanilib, bu tushunchalarning ahamiyatini tekshirish uchun vosita bo'lib xizmat qildi. Bu holat bugungi kungacha davom etmoqda.

Shaklni ifodalash

bu yerda;;;…;;… qator a’zolari; - nth yoki qatorning umumiy atamasi cheksiz qator (seriya) deyiladi.

Agar seriya a'zolari:

I. Raqamlar qatori

1.1. Sonlar qatori haqida asosiy tushunchalar.

Raqamlar qatori shaklning yig'indisidir

, (1.1)

bu yerda ,,,…,,... qator a'zolari deb ataladi, cheksiz ketma-ketlikni hosil qiladi; atama qatorning umumiy hadi deyiladi.

(1.1) qatorning birinchi hadlaridan tuzilgan bu qatorning qisman yig’indilari deyiladi.

Har bir satr qisman yig'indilar ketma-ketligi bilan bog'lanishi mumkin .

Agar, sonning cheksiz o'sishi bilan n Agar qatorning qisman yig'indisi chegaraga moyil bo'lsa, u holda ketma-ket konvergent deb ataladi va raqam konvergent qatorning yig'indisi deb ataladi, ya'ni.

Bu yozuvga teng

.

Cheksiz o'sish bilan (1.1) seriyalarning qisman yig'indisi bo'lsa n chekli chegaraga ega bo'lmasa (yoki ga moyil bo'ladi), unda bunday qator deyiladi turlicha .

Agar qator konvergent , keyin yetarlicha katta uchun qiymati n qatorlar yig‘indisining taxminiy ifodasidir S.

Farq qatorning qolgan qismi deb ataladi. Agar qator yaqinlashsa, uning qoldig'i nolga moyil bo'ladi, ya'ni va aksincha, agar qoldiq nolga moyil bo'lsa, u holda qator yaqinlashadi.

1.2. Raqamlar qatoriga misollar.

Misol 1. Shakl seriyasi

(1.2)

chaqirdi geometrik .

Geometrik progressiyaning hadlaridan geometrik qator hosil bo'ladi.

Ma'lumki, uning birinchi yig'indisi n a'zolari Shubhasiz: bu n- qatorning qisman yig'indisi (1.2).

Mumkin holatlar:

Seriya (1.2) quyidagi shaklni oladi:

, qator farqlanadi;

Seriya (1.2) quyidagi shaklni oladi:

Cheklov yo'q, seriya farqlanadi.

- chekli son, qator yaqinlashadi.

- seriya farqlanadi.

Demak, bu qator ga yaqinlashadi va da ajraladi.

Misol 2. Shaklning ketma-ketligi

(1.3)

chaqirdi garmonik .

Keling, ushbu qatorning qisman yig'indisini yozamiz:

Miqdori quyidagicha ko'rsatilgan miqdordan kattaroqdir:

yoki .

Agar , keyin , yoki .

Shuning uchun, agar , keyin , ya'ni. garmonik qator ajraladi.

Misol 3. Shaklning ketma-ketligi

(1.4)

chaqirdi umumlashtirilgan garmonik .

Agar , u holda bu qator divergent bo'lgan garmonik qatorga aylanadi.

Agar bo'lsa, bu qatorning hadlari garmonik qatorning tegishli hadlaridan katta bo'ladi va shuning uchun u ajralib chiqadi. Bizda geometrik qator mavjud bo'lganda; u konvergent hisoblanadi.

Demak, umumlashgan garmonik qator ga yaqinlashadi va da ajraladi.

1.3. Konvergentsiyaning zaruriy va yetarli mezonlari.

Seriya yaqinlashuvining zaruriy belgisi.

Agar qator cheksiz ortib borishi bilan uning umumiy hadi nolga moyil bo'lsagina yaqinlashishi mumkin: .

Agar bo'lsa, u holda ketma-ket ajraladi - bu ketma-ketlikning ajralishining etarli belgisidir.

Ijobiy shartlarga ega bo'lgan qator yaqinlashuvining etarli belgilari.

Seriyalarni ijobiy shartlar bilan taqqoslash belgisi.

O'rganilayotgan qator yaqinlashadi, agar uning shartlari boshqa, aniq yaqinlashuvchi qatorning tegishli shartlaridan oshmasa; o'rganilayotgan qator ajraladi, agar uning a'zolari boshqa, aniq divergent qatorning mos a'zolaridan oshsa.

D'Alembert belgisi.

Agar ijobiy shartlarga ega seriya uchun

shart qanoatlansa, qator ga yaqinlashadi va da ajraladi.

Agar D'Alembert testi javob bermaydi. Bunday holda, seriyani o'rganish uchun boshqa texnikalar qo'llaniladi.

Mashqlar.

Berilgan umumiy atama asosida qator yozing:

,,,… deb faraz qilsak, bizda cheksiz sonlar ketma-ketligi bor:

Uning shartlarini qo'shib, biz seriyani olamiz

.

Xuddi shunday qilib, biz seriyani olamiz

.

1,2,3,... qiymatlarini berib, shuni hisobga olsak,,,... qatorni olamiz

.

Toping n- Seriyaning birinchi a'zolariga ko'ra, a'zosi:

Birinchisidan boshlab qator shartlarining maxrajlari juft sonlar; shuning uchun, n- Seriyaning uchinchi qismi shaklga ega.

Ketma a'zolarining ayirgichlari sonlarning natural qatorini, mos keluvchi maxrajlari esa natural sonlar qatorini, mos keluvchi maxrajlari esa 3 dan boshlanadigan natural son qatorini hosil qiladi. Belgilar qonunga muvofiq yoki qonunga muvofiq almashinadi. qonunga. Ma'nosi, n- qatorning th a'zosi shaklga ega. yoki .

Kerakli konvergentsiya testi va taqqoslash testi yordamida qatorlarning yaqinlashuvini o'rganing:

;

.

topamiz .

Ketma-ket yaqinlashuvining zaruriy mezoni qanoatlantirildi, lekin yaqinlashuv masalasini hal qilish uchun yaqinlashuvning yetarli mezonlaridan birini qo‘llash zarur. Keling, bu qatorni geometrik qator bilan taqqoslaylik

,

buyon birlashadi.

Ushbu qatorning hadlarini ikkinchisidan boshlab, geometrik qatorning tegishli hadlari bilan taqqoslab, biz tengsizliklarni olamiz

bular. ikkinchisidan boshlab bu qatorning hadlari mos ravishda geometrik qatorning hadlaridan kichikroqdir, ya'ni bu qator yaqinlashadi.

.

Bu erda ketma-ketlikning divergentsiyasining etarli mezoni qondiriladi; shuning uchun qatorlar ajralib chiqadi.

topamiz .

Seriyaning yaqinlashishi uchun zarur bo'lgan mezon qondiriladi. Keling, bu qatorni umumlashtirilgan garmonik qator bilan taqqoslaylik

,

yaqinlashadi, chunki, demak, berilgan qator ham yaqinlashadi.

D'Alember testi yordamida qatorlarning yaqinlashuvini o'rganing:

;

.

Buning o'rniga qatorning umumiy atamasi bilan almashtirish n raqam n+ 1, biz olamiz. ga nisbatining chegarasi topilsin n- mu a'zosi:

Shunday qilib, bu seriya birlashadi.

Bu shuni anglatadiki, bu seriya bir-biridan farq qiladi.

Bular. qator ajralib chiqadi.

II. O'zgaruvchan seriyalar

2.1 O‘zgaruvchan qatorlar tushunchasi.

Raqamlar seriyasi

chaqirdi o'zgaruvchan belgi , agar uning a'zolari orasida ham ijobiy, ham salbiy raqamlar mavjud bo'lsa.

Raqamlar qatori deyiladi signal beruvchi , agar ikkita qo'shni atama qarama-qarshi belgilarga ega bo'lsa.

qayerda hamma uchun (ya'ni, ijobiy va salbiy atamalar o'z navbatida bir-birini kuzatib turadigan qator). Masalan,

;

;

.

Belgilari almashinadigan qatorlar uchun yaqinlashuvning etarli belgisi mavjud (1714 yilda Leybnits I. Bernulliga yozgan maktubida asos solgan).

2.2 Leybnits testi. Ketmalarning mutlaq va shartli yaqinlashuvi.

Teorema (Leybnits testi).

Muqobil qator yaqinlashadi, agar:

Seriya shartlarining mutlaq qiymatlari ketma-ketligi monoton ravishda kamayadi, ya'ni. ;

Seriyaning umumiy atamasi nolga intiladi:.

Bunda qatorning S yig’indisi tengsizliklarni qanoatlantiradi

Eslatmalar.

Shaklning o'zgaruvchan seriyasini o'rganish

(salbiy birinchi had bilan) qatorni o'rganish uchun uning barcha shartlarini ko'paytirish orqali kamayadi .

Leybnits teoremasining shartlari qanoatlantirilgan qatorlar deyiladi Leybnizchi (yoki Leybnits seriyasi).

Nisbat bizga summani almashtirishda yo'l qo'ygan xatoning oddiy va qulay bahosini olish imkonini beradi S berilgan qatorning qisman yig'indisi bo'yicha.

Tashlab qo'yilgan qator (qolgan) ham o'zgaruvchan qatordir , modul bo'yicha yig'indisi ushbu qatorning birinchi hadidan kichik, ya'ni, shuning uchun xato tashlangan hadlarning birinchisining modulidan kichikdir.

Misol. Taxminan qatorlar yig'indisini hisoblang.

Yechish: bu qator Leybnits tipidagi. Bu mos keladi. Siz yozishingiz mumkin:

.

Besh a'zoni olish, ya'ni. almashtirilishi mumkin

Keling, kichikroq xato qilaylik

Qanaqasiga . Shunday qilib,.

Muqobil qatorlar uchun yaqinlashuv uchun quyidagi umumiy etarli mezon amal qiladi.

Teorema. Muqobil qator berilsin

Agar qator yaqinlashsa

berilgan qator hadlarining modullaridan tuzilgan bo'lsa, keyin o'zgaruvchan qatorning o'zi yaqinlashadi.

Almashtiruvchi belgilar qatori uchun Leybnitsning yaqinlashuv testi oʻzgaruvchan belgilar qatorlarining yaqinlashuvi uchun yetarli mezon boʻlib xizmat qiladi.

Muqobil qator deyiladi mutlaqo konvergent , agar uning a'zolarining mutlaq qiymatlaridan tashkil topgan qator yaqinlashsa, ya'ni. Har bir absolyut yaqinlashuvchi qator yaqinlashuvchidir.

Agar o'zgaruvchan qator yaqinlashsa, lekin uning shartlarining mutlaq qiymatlaridan tashkil topgan qator ajralib chiqsa, bu qator deyiladi. shartli ravishda (mutlaqo emas) konvergent.

2.3. Mashqlar.

Muqobil qatorlarni yaqinlashuvini (mutlaq yoki shartli) tekshiring:

Va

Shuning uchun, Leybnits mezoniga ko'ra, qatorlar yaqinlashadi. Keling, bu qator mutlaq yoki shartli yaqinlashishini bilib olaylik.

Qator Berilgan qatorning mutlaq qiymatlaridan tashkil topgan , bir-biridan ajralib turuvchi garmonik qatordir. Shuning uchun bu qator shartli ravishda yaqinlashadi.

Ushbu seriyaning shartlari mutlaq qiymatda monoton ravishda kamayadi:

, Lekin

.

Seriya bir-biridan ajralib turadi, chunki Leybnits testi o'rinli emas.

Leybnits testidan foydalanib, biz olamiz

;,

bular. qator yaqinlashadi.

.

Bu qaerda, birlashadigan shaklning geometrik qatoridir. Shuning uchun, bu seriya mutlaqo birlashadi.

Leybnits testidan foydalanib, biz bor

;

, ya'ni. qator yaqinlashadi.

Keling, ushbu qator shartlarining mutlaq qiymatlaridan tashkil topgan qatorni ko'rib chiqaylik:

, yoki

.

Bu bir-biridan ajralib turadigan umumiy garmonik qatordir. Shuning uchun bu qator shartli ravishda yaqinlashadi.

III. Funktsional diapazon

3.1. Funktsional qator tushunchasi.

A'zolari funksiya bo'lgan qator deyiladi funktsional :

Muayyan qiymatni berib, biz raqamlar qatorini olamiz

konvergent yoki divergent bo'lishi mumkin.

Agar olingan sonlar qatori yaqinlashsa, nuqta chaqiriladi konvergentsiya nuqtasi funktsional diapazon; agar qator ajralib chiqsa - ajralish nuqtasi funktsional diapazon.

Funktsional qatorlar yaqinlashadigan argumentning raqamli qiymatlari to'plami deyiladi konvergentsiya maydoni .

Funktsional qatorning yaqinlashish mintaqasida uning yig'indisi qandaydir funktsiyadir:.

U yaqinlashuv mintaqasida tenglik bilan aniqlanadi

, Qayerda

Seriyaning qisman yig'indisi.

Misol. Seriyaning yaqinlashish maydonini toping.

Yechim. Bu qator maxrajli geometrik progressiya qatoridir. Binobarin, bu qator ga yaqinlashadi, ya'ni. hammaning oldida; qatorning yig'indisi;

, da .

3.2. Quvvat seriyasi.

Quvvat qatori shaklning qatoridir

,

raqamlar qayerda chaqiriladi qator koeffitsientlari , va bu atama turkumning umumiy atamasi hisoblanadi.

Kuchli qatorning yaqinlashuv mintaqasi qator yaqinlashadigan barcha qiymatlar to'plamidir.

Raqam chaqiriladi yaqinlashish radiusi kuch qatori, agar qator yaqinlashsa va bundan tashqari, mutlaq va qator ajralib chiqsa.

D'Alember belgisi yordamida yaqinlashish radiusini topamiz:

(bog'liq emas)

bular. agar kuch qatori bu shartni qanoatlantiruvchi har qanday uchun yaqinlashsa va uchun diversiya qilsa.

Bundan kelib chiqadiki, agar chegara bo'lsa

,

u holda qatorning yaqinlashish radiusi bu chegaraga teng bo'ladi va kuch qatori ga yaqinlashadi, ya'ni. chaqirilgan intervalda yaqinlashish oralig'i (interval).

Agar bo'lsa, u holda kuch qatorlari bir nuqtada yaqinlashadi.

Intervalning oxirida qator yaqinlashishi mumkin (mutlaq yoki shartli), lekin u ham ajralib chiqishi mumkin.

va darajasidagi darajali qatorning yaqinlashuvi har qanday yaqinlashish testlari yordamida o'rganiladi.

3.3. Mashqlar.

Seriyaning yaqinlashish maydonini toping:

Yechim. Ushbu qatorning yaqinlashish radiusini topamiz:

.

Binobarin, bu qator mutlaqo butun son chizig'iga yaqinlashadi.

Yechim. Keling, d'Alember belgisidan foydalanamiz. Ushbu seriya uchun bizda:

.

Seriya, agar yoki bo'lsa, mutlaqo yaqinlashuvchidir. Keling, konvergentsiya oralig'i oxiridagi qatorlarning harakatini o'rganamiz.

Serial bizda bo'lganda

Serial bizda bo'lganda - bu ham Leybnitsning konvergent qatoridir. Binobarin, asl qatorning yaqinlashuv mintaqasi segment hisoblanadi.

Yechim. Keling, qatorning yaqinlashish radiusini topamiz:

Binobarin, qator yaqinlashadi, ya'ni. da.

Biz seriyani olamiz , bu Leybnits mezoniga muvofiq yaqinlashadi.

Biz divergent seriyani olamiz

.

Binobarin, dastlabki qatorning yaqinlashish mintaqasi intervaldir.

IV. Maklaurin seriyasida elementar funksiyalarni kengaytirish.

Ilovalar uchun ushbu funktsiyani quvvat seriyasiga kengaytira olish muhimdir, ya'ni. funktsiyani darajalar qatorining yig'indisi sifatida ifodalaydi.

Funksiya uchun Teylor qatori shaklning darajali qatoridir

Agar bo'lsa, biz Teylor seriyasining maxsus holatini olamiz

qaysi deyiladi Maklaurin yaqinida .

Konvergentsiya oralig'idagi darajali qatorni termin bo'yicha farqlash va xohlagancha ko'p marta integrallash mumkin va natijada olingan qatorlar asl qator bilan bir xil yaqinlashish oralig'iga ega.

Ko‘phadlarni qo‘shish va ko‘paytirish qoidalariga ko‘ra, ikkita darajali qator qo‘shilishi va hadga ko‘paytirilishi mumkin. Bunday holda, hosil bo'lgan yangi qatorning yaqinlashuv oralig'i dastlabki qatorning yaqinlashuv intervallarining umumiy qismiga to'g'ri keladi.

Funktsiyani Maclaurin seriyasiga kengaytirish uchun quyidagilar zarur:

Nuqtadagi funktsiya va uning ketma-ket hosilalari qiymatlarini hisoblang, ya'ni,,,...,;

Funktsiya qiymatlarini va uning ketma-ket hosilalarini Maklaurin qator formulasiga almashtirib, Maklaurin qatorini tuzing;

Formuladan foydalanib, hosil bo'lgan qatorning yaqinlashish oralig'ini toping

, .

Misol 1. Funktsiyani Maklaurin seriyasiga kengaytiring.

Yechim. Chunki , keyin kengaytirishda bilan almashtirsak, biz quyidagilarni olamiz:

2-misol. Funksiyaning Maklaurin qatorini yozing .

Yechim. Chunki , keyin bilan almashtirilgan formuladan foydalanib, biz quyidagilarni olamiz:

,

Misol 3. Maklaurin seriyasida funksiyani kengaytiring.

Yechim. Keling, formuladan foydalanamiz. Chunki

, keyin bilan almashtirsak, biz quyidagilarni olamiz:

, yoki

qayerda, ya'ni. .

V. Talabalarning o'z-o'zini nazorat qilish uchun amaliy topshiriqlar.

Qatorlarni taqqoslash uchun testdan foydalanib, yaqinlashishni o'rnating

shartli ravishda birlashadi;

shartli ravishda birlashadi;

mutlaqo birlashadi.

;

;

VII. Tarixiy ma'lumotnoma.

Ko'pgina muammolarni hal qilish funktsiyalar va integrallarning qiymatlarini hisoblash yoki noma'lum funktsiyalarning hosilalari yoki differentsiallarini o'z ichiga olgan differensial tenglamalarni echish bilan bog'liq.

Biroq, bu matematik amallarning aniq bajarilishi ko'p hollarda juda qiyin yoki imkonsiz bo'lib chiqadi. Bunday hollarda ketma-ketlik yordamida istalgan aniqlikdagi ko'plab masalalarning taxminiy yechimini olish mumkin.

Seriyalar – funksiyalarni, integrallarni va differentsial tenglamalar yechimlarini taxminiy hisoblash uchun matematik tahlilning sodda va ilg‘or quroli.

Va o'ngdagi funktsional qator.

“” belgisini teng belgi bilan almashtirish uchun, xususan, tenglikning o'ng tomonidagi hadlar sonining cheksizligi va qatorning yaqinlashish mintaqasi bilan bog'liq ba'zi qo'shimcha mulohazalarni bajarish kerak.

Teylor formulasi Maklaurin formulasi deb ataladigan shaklni olganida:

Nyutonning shogirdi Kolin Maklaurin (1698 - 1746) o'zining "Flyuksiyalar haqida risola" (1742) asarida analitik funktsiyani ifodalovchi darajalar qatori yagona ekanligini va u bunday funktsiya tomonidan yaratilgan Teylor qatori bo'lishini aniqladi. . Nyuton binomial formulasida kuchlarning koeffitsientlari qiymatlardir, bu erda .

Shunday qilib, saflar 18-asrda paydo bo'ldi. cheksiz farqlash imkonini beruvchi funktsiyalarni ifodalash usuli sifatida. Biroq, qator bilan ifodalangan funktsiya uning yig'indisi deb atalmagan va umuman olganda, o'sha paytda sonli yoki funktsional qatorning yig'indisi nima ekanligi aniqlanmagan, faqat bu tushunchani kiritishga urinishlar bo'lgan.

Masalan, L. Eyler (1707-1783) funktsiya uchun mos darajali qatorni yozib, o'zgaruvchiga o'ziga xos qiymat berdi. Natijada raqamlar seriyasi paydo bo'ldi. Eyler bu qatorning yig’indisini nuqtadagi dastlabki funksiyaning qiymati deb hisobladi. Lekin bu har doim ham to'g'ri emas.

Olimlar divergent qatorning yig'indisi yo'qligini faqat 19-asrda, garchi 18-asrda bo'lsa ham tushuna boshladilar. ko'pchilik va birinchi navbatda L. Eyler konvergentsiya va divergensiya tushunchalari ustida ko'p ishladilar. Eyler ketma-ketlikni konvergent deb atadi, agar uning umumiy atamasi nolga teng bo'lsa.

Divergent qatorlar nazariyasida Eyler ko'plab muhim natijalarga erishdi, ammo bu natijalar uzoq vaqt davomida qo'llanilmadi. 1826 yilda N.G. Abel (1802 - 1829) turli xil seriyalarni "iblisning ixtirosi" deb atadi. Eylerning natijalari 19-asr oxiridagina isbotlangan.

Konvergent qatorlar yig‘indisi tushunchasining shakllanishida fransuz olimi O.L. Koshi (1789-1857); u nafaqat qatorlar nazariyasida, balki chegaralar nazariyasida, chegara tushunchasini ishlab chiqishda ham juda katta ishlarni amalga oshirdi. 1826 yilda Koshining ta'kidlashicha, divergent qatorning yig'indisi yo'q.

1768 yilda Fransuz matematigi va faylasufi J.L. D'Alember binomial qatorda keyingi hadning oldingisiga nisbatini o'rganib chiqdi va agar bu nisbat mutlaq qiymatda birdan kichik bo'lsa, unda qator yaqinlashishini ko'rsatdi. Koshi 1821 yilda musbat qatorlarning yaqinlashuvi uchun testni umumiy shaklda ifodalovchi teoremani isbotladi, hozirda D'Alembert testi deb ataladi.

O'zgaruvchan qatorlarning yaqinlashuvini o'rganish uchun Leybnits testi qo'llaniladi.

G.V. Buyuk nemis matematiki va faylasufi Leybnits (1646 – 1716) I. Nyuton bilan birga differensial va integral hisoblarning asoschisidir.

Adabiyotlar ro'yxati:

Asosiy:

1. Bogomolov N.V., Matematikadan amaliy darslar. M., “Oliy maktab”, 1990 – 495 b.;
2. Tarasov N.P., Texnik maktablar uchun oliy matematika kursi. M., “Fan”, 1971 – 448 b.;
3. Zaitsev I.L., Texnik maktablar uchun oliy matematika kursi. M., texnikumlar davlat nashriyoti - nazariy adabiyotlar, 1957 - 339 b.;
4. Pismenny D.T., Oliy matematika bo'yicha ma'ruzalar kursi. M., "Iris Press", 2005 yil, 2-qism - 256 b.;
5. Vygodskiy M.Ya., Oliy matematika bo'yicha qo'llanma. M., “Fan”, 1975 – 872 b.;

Qo'shimcha:

1. Gusak A.A., Oliy matematika. 2 jildda, T.2: Universitet talabalari uchun darslik. Mos., "TetraSystems", 1988 - 448 p.;
2. Griguletskiy V.G., Lukyanova I.V., Petunina I.A., Iqtisodiyot mutaxassisliklari talabalari uchun matematika. 2-qism. Krasnodar, 2002 yil - 348 pp.;
3. Griguletskiy V.G. va hokazo matematikadan muammoli kitob. Krasnodar. KSAU, 2003 yil - 170 b.;
4. Griguletskiy V.G., Stepantsova K.G., Getman V.N., Buxgalteriya hisobi va moliya fakulteti talabalari uchun vazifalar va mashqlar. Krasnodar. 2001 yil – 173 b.;
5. Griguletskiy V.G., Yashchenko Z.V., Oliy matematika. Krasnodar, 1998 yil - 186 pp.;
6. Malykhin V.I., Iqtisodiyotda matematika. M., "Infra-M", 1999 - 356 b.

Ushbu mavzuda biz qatorlarni yaqinlashtirish uchun zarur bo'lgan mezon, D'Alembert va Koshi testlari, shuningdek, taqqoslash testlari o'rtasida tanlov qilishingiz mumkin bo'lgan ba'zi bir mezonlarni ko'rib chiqamiz.Shuni eslatib o'taman. , shuningdek, integral va radikal Koshi testlari faqat musbat sonli qatorlar uchun qo‘llaniladi (ya’ni umumiy atamasi noldan kam bo‘lmagan qatorlar, $u_n≥ 0$).D’Alember testi qat’iy musbat qatorlar uchun qo‘llaniladi ($u_n). > 0$).

Raqamlar qatorining yaqinlashuvini tekshirish uchun mezonni tanlash, umuman olganda, oson ish emas. Biroq, standart standart hisob-kitoblar va nazorat ishlarida qo'llaniladigan seriyalar uchun ba'zi umumiy tavsiyalar berilishi mumkin. Men ushbu tavsiyalarni jadvalga yozaman.

Jadvalning o'zi haqida bir necha so'z. Ikkinchi ustun ko'pgina standart testlarda ma'lum bir konvergentsiya mezonini qo'llash doirasini tavsiflaydi. Uchinchi ustunda ikkinchi ustundagi ma'lumotlar illyustrativ misollar bilan tasvirlangan (barcha bu misollar tegishli mavzularda echilgan). To'rtinchi ustunda umumiy sxemadan biroz tashqarida bo'lgan yoki standart test qog'ozlarida tez-tez uchramaydigan seriyalar misollari mavjud.

Ism	Asosiy dastur	Qatorlarga misollar	Qo'shimcha foydalanish
Konvergentsiyaning zaruriy belgisi	Ketmaning umumiy hadi kasr bilan ifodalanadi, uning soni va maxraji ma'lum ko'phadlardir. Yoki polinomlarning ildizlari bo'lishi mumkin. Kerakli yaqinlashish shartidan foydalanib, ixtiyoriy sonlar qatorining farqlanishini isbotlash mumkin (musbat bo'lishi shart emas).	$\sum\limits_(n=1)^(\infty)\frac(3n^2+2n-1)(5n^2+7)$, $\sum\limits_(n=1)^(\infty) \frac(\sqrt(4n^7+5n^3-4))(9n^2-n+12)$.	$\sum\limits_(n=1)^(\infty)\left(5^n\sin\frac(8)(3^n)\o'ng)$, $\sum\limits_(n=1)^( \infty)\frac(3^n)(n^2)$, $\sum\limits_(n=1)^(\infty)\left(\frac(2n+7)(2n+3)\o'ng) ^(9n+1)$, $\sum\limits_(n=1)^(\infty)\sin n$, $\sum\limits_(n=1)^(\infty)\frac(1-\cos) \frac(1)(n))(\ln\left(1+\frac(1)(n^2)\o'ng))$, $\sum\limits_(n=1)^(\infty)(- 1)^n\frac(17n^5+4\cos(n!))(6n^5+2n^2-1)$.
Taqqoslash belgilari	Ketmaning umumiy hadi kasr bilan ifodalanadi, uning soni va maxraji ma'lum ko'phadlardir. Yoki ko'phadlar o'rniga (yoki ular bilan birga) ko'phadning ildizlari mavjud bo'lishi mumkin. Ushbu turdagi qatorlar uchun yaqinlashuv uchun zarur bo'lgan mezon va taqqoslash mezonlari o'rtasida tanlov qilish kerak. Ketma-ketdagi umumiy atama nafaqat ko'phadni, balki konvergentsiyaga ta'sir qilmaydigan qandaydir "chalg'ituvchi element" ni ham o'z ichiga olishi mumkin. Ba'zan, taqqoslash uchun qatorni ko'rish uchun siz ekvivalent cheksiz kichik funktsiyalardan foydalanishingiz kerak.	$\sum\limits_(n=1)^(\infty)\frac(9n+7)(2n^3+5n^2-4)$, $\sum\limits_(n=1)^(\infty) \frac(4n^3+2n+9)(n^2(3n+5)^2)$, $\sum\limits_(n=1)^(\infty)\frac(5n^2-3)( \sqrt(7n^(10)+2n^3-4))$, $\sum\limits_(n=1)^(\infty)\frac(\arcsin\frac(7n-1)(9n))( \sqrt(4n^2-3))$, $\sum\limits_(n=1)^(\infty)\frac(\arctg^2\sqrt(2n^3-1))(\sqrt(3n^) 5-2))$, $\sum\limits_(n=1)^(\infty)\frac(1)(n)\sin\left(\frac(2+(-1)^n)(6) \cdot\pi\right)$, $\sum\limits_(n=1)^(\infty)\frac(2^(3n)+\cos n{5^{2n+1}-n}$, $\sum\limits_{n=1}^{\infty}\frac{1}{\sqrt{n}}\arctg\frac{\pi}{\sqrt{2n-1}}$, $\sum\limits_{n=1}^{\infty}\left(1-\cos\frac{7}{n}\right)$, $\sum\limits_{n=1}^{\infty}n\left(e^\frac{3}{n}-1\right)^2$, $\sum\limits_{n=1}^{\infty}\ln\frac{n^3+7}{n^3+5}$. !}	$\sum\limits_(n=1)^(\infty)\left(\sqrt(2n+3)-\sqrt(2n-1)\o'ng)$, $\sum\limits_(n=1)^( \infty)\frac(n^n)(7^n\cdot n$. !}
D'Alembert belgisi	Seriyaning umumiy hadi ifodasi koʻphadni (koʻphad ildiz ostida ham boʻlishi mumkin) va $a^n$ yoki $n!$ koʻrinishidagi darajani oʻz ichiga oladi. Yoki qatorning umumiy atamasi quyidagi shakldagi hosilani o'z ichiga oladi: $3\cdot 5\cdot 7\cdot\ldots\cdot(2n+1)$.	$\sum\limits_(n=1)^(\infty)\frac(5^n\cdot(3n+7))(2n^3-1)$, $\sum\limits_(n=1)^( \infty)\frac(\sqrt(4n+5))((3n-2)$, $\sum\limits_{n=1}^{\infty}\frac{(2n+5)!}{4^{3n+2}}$, $\sum\limits_{n=1}^{\infty}\frac{n^n}{3^n\cdot n!}$, $\sum\limits_{n=1}^{\infty}\frac{6^{2n+5}\left(3n^2-1\right)}{(n+3)!}$, $\sum\limits_{n=1}^{\infty}\frac{3\cdot 5\cdot 7\cdot\ldots\cdot(2n+1)}{2\cdot 5\cdot 8\cdot\ldots\cdot(3n-1)}$, $\sum\limits_{n=1}^{\infty}\frac{1\cdot 11\cdot 21\cdot\ldots\cdot(10n-9)}{(2n-1)!!}$. !}	$\sum\limits_(n=1)^(\infty)\frac(4n-1)(n)\sin\frac(2)(3^n)$, $\sum\limits_(n=1)^ (\infty)\frac(3^(2n+1)-4)(2^(5n)(n+1)$, $\sum\limits_{n=1}^{\infty}\frac{\left(n!\right)^2}{2^{n^2}}$. !}
Radikal Koshi belgisi	Seriyaning umumiy termini ifodasida barcha elementlar $n$ ga kamaytirilishi mumkin bo'lgan quvvatga ko'tariladi.	$\sum\limits_(n=1)^(\infty)\left(\frac(3n^2-1)(5n^2+7n)\o'ng)^(2n)$, $\sum\limits_(n) =1)^(\infty)\left(\frac(2n+3)(7n-5)\o'ng)^(n^2)$, $\sum\limits_(n=1)^(\infty)\ chap(\frac(2n+1)(2n-1)\o'ng)^(n(3n+4))$, $\sum\limits_(n=1)^(\infty)\frac((5n+4) )^n)(7^(2n)\cdot n^n)$, $\sum\limits_(n=1)^(\infty)\left(\sin\frac(4)(n^2+2n) \ o'ng) ^ (\ frac (n) (2)) $.	$\sum\limits_(n=1)^(\infty)\frac(\left(3n^2+7\o'ng)\cdot 5^(2n-1))(4^n)$, $\sum\ chegaralar_(n=1)^(\infty)\frac(n^n)(7^n\cdot n$. !}

Ushbu maqola mashqlar va vazifalarni tahlil qilishda foydali bo'lishi mumkin bo'lgan tuzilgan va batafsil ma'lumotlarni taqdim etadi. Biz raqamlar qatori mavzusini ko'rib chiqamiz.

Ushbu maqola asosiy ta'riflar va tushunchalar bilan boshlanadi. Keyinchalik, biz standart variantlardan foydalanamiz va asosiy formulalarni o'rganamiz. Materialni mustahkamlash uchun maqolada asosiy misollar va vazifalar berilgan.

Asosiy tezislar

Birinchidan, tizimni tasavvur qilaylik: a 1 , a 2 . . . , a n ,. . . , bu yerda a k ∈ R, k = 1, 2. . . .

Masalan, 6, 3, - 3 2, 3 4, 3 8, - 3 16, kabi raqamlarni olaylik. . . .

Ta'rif 1

Raqamlar qatori ∑ a k k = 1 ∞ = a 1 + a 2 + hadlar yig'indisidir. . . + a n +. . . .

Ta'rifni yaxshiroq tushunish uchun q = - 0 bo'lgan ushbu holatni ko'rib chiqing. 5: 8 - 4 + 2 - 1 + 1 2 - 1 4 +. . . = ∑ k = 1 ∞ (- 16) · - 1 2 k .

Ta'rif 2

a k umumiy yoki k –chi seriyasining a'zosi.

Bu shunday ko'rinadi - 16 · - 1 2 k.

Ta'rif 3

Seriyalarning qisman yig'indisi shunga o'xshash narsa ko'rinadi S n = a 1 + a 2 + . . . + a n , unda n- har qanday raqam. S n nth qator yig'indisi.

Masalan, ∑ k = 1 ∞ (- 16) · - 1 2 k S 4 = 8 - 4 + 2 - 1 = 5 ga teng.

S 1 , S 2 ,. . . , S n, . . . cheksiz sonlar ketma-ketligini hosil qiladi.

Bir qator uchun nth yig'indi S n = a 1 · (1 - q n) 1 - q = 8 · 1 - - 1 2 n 1 - - 1 2 = 16 3 · 1 - - 1 2 n formula bo'yicha topiladi. Biz qisman yig'indilarning quyidagi ketma-ketligini ishlatamiz: 8, 4, 6, 5, . . . , 16 3 · 1 - - 1 2 n,. . . .

Ta'rif 4

∑ k = 1 ∞ a k qator konvergent ketma-ketlik chekli chegaraga ega bo'lganda S = lim S n n → + ∞ . Agar chegara bo'lmasa yoki ketma-ketlik cheksiz bo'lsa, u holda ∑ k = 1 ∞ a k qator deyiladi. turlicha.

Ta'rif 5

Konvergent qator yig'indisi∑ k = 1 ∞ a k - ketma-ketlikning chegarasi ∑ k = 1 ∞ a k = lim S n n → + ∞ = S.

Bu misolda lim S n n → + ∞ = lim 16 3 t → + ∞ · 1 - 1 2 n = 16 3 · lim n → + ∞ 1 - - 1 2 n = 16 3 , qator ∑ k = 1 ∞ ( - 16) · - 1 2 k yaqinlashadi. Yig'indi 16 3 ga teng: ∑ k = 1 ∞ (- 16) · - 1 2 k = 16 3 .

1-misol

Divergent qatorlarga maxraji birdan katta bo'lgan geometrik progressiyaning yig'indisi misol bo'la oladi: 1 + 2 + 4 + 8 +. . . + 2 n - 1 +. . . = ∑ k = 1 ∞ 2 k - 1.

n-chi qisman yig'indi S n = a 1 (1 - q n) 1 - q = 1 (1 - 2 n) 1 - 2 = 2 n - 1 bilan berilgan va qisman yig'indilarning chegarasi cheksizdir: lim n → + ∞ S n = lim n → + ∞ (2 n - 1) = + ∞ .

Divergent sonlar qatoriga yana bir misol ∑ k = 1 ∞ 5 = 5 + 5 + ko'rinishdagi yig'indidir. . . . Bunday holda, n-chi qisman yig'indini Sn = 5n sifatida hisoblash mumkin. Qisman yig'indilarning chegarasi cheksiz lim n → + ∞ S n = lim n → + ∞ 5 n = + ∞.

Ta'rif 6

∑ k = 1 ∞ = 1 + 1 2 + 1 3 + bilan bir xil shakldagi yig'indi. . . + 1 n +. . . - Bu garmonik raqamlar seriyasi.

Ta'rif 7

Yig'indi ∑ k = 1 ∞ 1 k s = 1 + 1 2 s + 1 3 s +. . . + 1 n s + . . . , Qayerda s– haqiqiy son, umumlashgan garmonik sonlar qatori.

Yuqorida muhokama qilingan ta'riflar sizga ko'pgina misollar va muammolarni hal qilishga yordam beradi.

Ta'riflarni to'ldirish uchun ma'lum tenglamalarni isbotlash kerak.

1. ∑ k = 1 ∞ 1 k – divergent.

Biz teskari usuldan foydalanamiz. Agar u yaqinlashsa, chegara cheklangan. Tenglamani lim n → + ∞ S n = S va lim n → + ∞ S 2 n = S shaklida yozishimiz mumkin. Muayyan harakatlardan keyin l i m n → + ∞ (S 2 n - S n) = 0 tengligini olamiz.

qarshi,

S 2 n - S n = 1 + 1 2 + 1 3 +. . . + 1 n + 1 n + 1 + 1 n + 2 +. . . + 1 2 n - - 1 + 1 2 + 1 3 +. . . + 1 n = 1 n + 1 + 1 n + 2 +. . . + 1 2 n

Quyidagi tengsizliklar o‘rinli: 1 n + 1 > 1 2 n, 1 n + 1 > 1 2 n, . . . , 1 2 n - 1 > 1 2 n. Biz S 2 n - S n = 1 n + 1 + 1 n + 2 + ni olamiz. . . + 1 2 n > 1 2 n + 1 2 n +. . . + 1 2 n = n 2 n = 1 2. S 2 n - S n > 1 2 ifodasi lim n → + ∞ (S 2 n - S n) = 0 ga erishilmasligini bildiradi. Seriya turlicha.

1. b 1 + b 1 q + b 1 q 2 +. . . + b 1 q n +. . . = ∑ k = 1 ∞ b 1 q k - 1

Raqamlar ketma-ketligi yig'indisi q da yaqinlashishini tasdiqlash kerak< 1 , и расходится при q ≥ 1 .

Yuqoridagi ta'riflarga ko'ra, miqdor n atamalar S n = b 1 · (q n - 1) q - 1 formulasi bo'yicha aniqlanadi.

Agar q< 1 верно

lim n → + ∞ S n = lim n → + ∞ b 1 · q n - 1 q - 1 = b 1 · lim n → + ∞ q n q - 1 - lim n → + ∞ 1 q - 1 = = b 1 · 0 - 1 q - 1 = b 1 q - 1

Biz sonlar qatorining yaqinlashishini isbotladik.

q = 1 b 1 + b 1 + b 1 + uchun. . . ∑ k = 1 ∞ b 1. Yig'indilarni S n = b 1 · n formulasi yordamida topish mumkin, chegara cheksiz lim n → + ∞ S n = lim n → + ∞ b 1 · n = ∞. Taqdim etilgan versiyada seriyalar ajralib turadi.

Agar q = - 1, keyin qator b 1 - b 1 + b 1 - kabi ko'rinadi. . . = ∑ k = 1 ∞ b 1 (- 1) k + 1 . Qisman summalar toq uchun S n = b 1 ga o'xshaydi n, va juftlik uchun S n = 0 n. Ushbu ishni ko'rib chiqqach, biz hech qanday chegara yo'qligiga va ketma-ketlik divergentligiga ishonch hosil qilamiz.

q > 1 uchun lim n → + ∞ S n = lim n → + ∞ b 1 · (q n - 1) q - 1 = b 1 · lim n → + ∞ q n q - 1 - lim n → + ∞ 1 q - 1 = = b 1 ∞ - 1 q - 1 = ∞

Biz raqamlar qatori bir-biridan farq qilishini isbotladik.

1. ∑ k = 1 ∞ 1 k s qator yaqinlashadi, agar s > 1 va agar s ≤ 1 bo'lsa, ajralib chiqadi.

Uchun s = 1 biz ∑ k = 1 ∞ 1 k ni olamiz, qator uzoqlashadi.

Qachon s< 1 получаем 1 k s ≥ 1 k для k, natural son. Seriya divergent ∑ k = 1 ∞ 1 k bo'lgani uchun chegara yo'q. Shundan keyin ∑ k = 1 ∞ 1 k s ketma-ketlik chegaralanmagan. Biz tanlangan qator qachon farqlanadi, degan xulosaga keldik s< 1 .

∑ k = 1 ∞ 1 k s qatorning yaqinlashishiga dalil keltirish kerak. s > 1.

S 2 n - 1 - S n - 1 ni tasavvur qilaylik:

S 2 n - 1 - S n - 1 = 1 + 1 2 s + 1 3 s +. . . + 1 (n - 1) s + 1 n s + 1 (n + 1) s + . . . + 1 (2 n - 1) s - - 1 + 1 2 s + 1 3 s + . . . + 1 (n - 1) s = 1 n s + 1 (n + 1) s + . . . + 1 (2 n - 1) s

Faraz qilaylik, 1 (n + 1) s< 1 n s , 1 (n + 2) s < 1 n s , . . . , 1 (2 n - 1) s < 1 n s , тогда S 2 n - 1 - S n - 1 = 1 n s + 1 (n + 1) s + . . . + 1 (2 n - 1) s < < 1 n s + 1 n s + . . . + 1 n s = n n s = 1 n s - 1

Tabiiy va hatto n = 2 bo'lgan sonlar uchun tenglamani tasavvur qilaylik: S 2 n - 1 - S n - 1 = S 3 - S 1 = 1 2 s + 1 3 s.< 1 2 s - 1 n = 4: S 2 n - 1 - S n - 1 = S 7 - S 3 = 1 4 s + 1 5 s + 1 6 s + 1 7 s < 1 4 s - 1 = 1 2 s - 1 2 n = 8: S 2 n - 1 - S n - 1 = S 15 - S 7 = 1 8 s + 1 9 s + . . . + 1 15 s < 1 8 s - 1 = 1 2 s - 1 3 . . .

Biz olamiz:

∑ k = 1 ∞ 1 k s = 1 + 1 2 s + 1 3 s + 1 4 s +. . . + 1 7 s + 1 8 s + . . . + 1 15 s +. . . = = 1 + S 3 - S 1 + S 7 - S 3 + S 15 + S 7 +. . .< < 1 + 1 2 s - 1 + 1 2 s - 1 2 + 1 2 s - 1 3 + . . .

Ifodasi 1 + 1 2 s - 1 + 1 2 s - 1 2 + 1 2 s - 1 3 +. . . q = 1 2 s - 1 geometrik progressiyaning yig'indisidir. Dastlabki ma'lumotlarga ko'ra s > 1, keyin 0< q < 1 . Получаем, ∑ k = 1 ∞ < 1 + 1 2 s - 1 + 1 2 s - 1 2 + 1 2 s - 1 3 + . . . = 1 1 - q = 1 1 - 1 2 s - 1 . Последовательность ряда при s > 1 ortadi va 1 1 - 1 2 s - 1 dan yuqoridan cheklanadi. Tasavvur qilaylik, chegara bor va qator yaqinlashuvchi ∑ k = 1 ∞ 1 k s .

Ta'rif 8

Seriya ∑ k = 1 ∞ a k u holda ijobiydir, agar uning a'zolari > 0 a k > 0 bo'lsa, k = 1, 2,. . . .

Seriya ∑ k = 1 ∞ b k signal beruvchi, agar raqamlarning belgilari boshqacha bo'lsa. Bu misol ∑ k = 1 ∞ b k = ∑ k = 1 ∞ (- 1) k · a k yoki ∑ k = 1 ∞ b k = ∑ k = 1 ∞ (- 1) k + 1 · a k , bu erda a k > 0, k = 1, 2,. . . .

Seriya ∑ k = 1 ∞ b k muqobil, chunki u ko'p sonlarni o'z ichiga oladi, salbiy va ijobiy.

Ikkinchi variant seriyasi uchinchi variantning alohida holatidir.

Quyida har bir holat uchun misollar keltirilgan:

6 + 3 + 3 2 + 3 4 + 3 8 + 3 16 + . . . 6 - 3 + 3 2 - 3 4 + 3 8 - 3 16 + . . . 6 + 3 - 3 2 + 3 4 + 3 8 - 3 16 + . . .

Uchinchi variant uchun siz mutlaq va shartli yaqinlashuvni ham aniqlashingiz mumkin.

Ta'rif 9

∑ k = 1 ∞ b k qatori ∑ k = 1 ∞ b k ham yaqinlashuvchi deb hisoblangan holatda mutlaqo yaqinlashuvchidir.

Keling, bir nechta odatiy variantlarni batafsil ko'rib chiqaylik.

2-misol

Agar qatorlar 6 - 3 + 3 2 - 3 4 + 3 8 - 3 16 + bo'lsa. . . va 6 + 3 - 3 2 + 3 4 + 3 8 - 3 16 +. . . konvergent sifatida aniqlanadi, u holda 6 + 3 + 3 2 + 3 4 + 3 8 + 3 16 + deb taxmin qilish to'g'ri bo'ladi. . .

Ta'rif 10

O‘zgaruvchan ∑ k = 1 ∞ b k qator shartli yaqinlashuvchi hisoblanadi, agar ∑ k = 1 ∞ b k divergent bo‘lsa, ∑ k = 1 ∞ b k qator esa yaqinlashuvchi hisoblanadi.

3-misol

∑ k = 1 ∞ (- 1) k + 1 k = 1 - 1 2 + 1 3 - 1 4 + variantini batafsil ko'rib chiqamiz. . . . Mutlaq qiymatlardan tashkil topgan ∑ k = 1 ∞ (- 1) k + 1 k = ∑ k = 1 ∞ 1 k qator divergent sifatida aniqlanadi. Bu variant konvergent hisoblanadi, chunki uni aniqlash oson. Bu misoldan biz ∑ k = 1 ∞ (- 1) k + 1 k = 1 - 1 2 + 1 3 - 1 4 + qatorini bilib olamiz. . . shartli konvergent hisoblanadi.

Konvergent qatorlarning xususiyatlari

Keling, ayrim holatlar uchun xususiyatlarni tahlil qilaylik

1. Agar ∑ k = 1 ∞ a k yaqinlashsa, u holda ∑ k = m + 1 ∞ a k qator ham yaqinlashuvchi hisoblanadi. Bu holda qator ekanligini ta'kidlash mumkin m atamalar ham konvergent hisoblanadi. Agar ∑ k = m + 1 ∞ a k ga bir nechta son qo'shsak, natijada olingan natija ham yaqinlashuvchi bo'ladi.
2. Agar ∑ k = 1 ∞ a k yaqinlashadi va yig'indi = S, u holda ∑ k = 1 ∞ A · a k, ∑ k = 1 ∞ A · a k = A · S qatorlari ham yaqinlashadi, bunda A-doimiy.
3. Agar ∑ k = 1 ∞ a k va ∑ k = 1 ∞ b k yaqinlashuvchi bo‘lsa, yig‘indilar A Va B ham, u holda ∑ k = 1 ∞ a k + b k va ∑ k = 1 ∞ a k - b k qatorlari ham yaqinlashadi. Miqdorlar teng bo'ladi A+B Va A - B mos ravishda.

4-misol

Qator ∑ k = 1 ∞ 2 3 k · k 3 ga yaqinlashishini aniqlang.

∑ k = 1 ∞ 2 3 k · k 3 = ∑ k = 1 ∞ 2 3 · 1 k 4 3 ifodani o‘zgartiramiz. ∑ k = 1 ∞ 1 k 4 3 qator yaqinlashuvchi hisoblanadi, chunki ∑ k = 1 ∞ 1 k s qator qachon yaqinlashadi s > 1. Ikkinchi xususiyatga ko'ra, ∑ k = 1 ∞ 2 3 · 1 k 4 3 .

5-misol

∑ n = 1 ∞ 3 + n n 5 2 qator yaqinlashishini aniqlang.

Keling, asl nusxani ∑ n = 1 ∞ 3 + n n 5 2 = ∑ n = 1 ∞ 3 n 5 2 + n n 2 = ∑ n = 1 ∞ 3 n 5 2 + ∑ n = 1 ∞1 ni o‘zgartiramiz.

Biz ∑ n = 1 ∞ 3 n 5 2 va ∑ n = 1 ∞ 1 n 2 yig‘indisini olamiz. Har bir qator xossaga ko'ra konvergent hisoblanadi. Shunday qilib, ketma-ketlik yaqinlashganda, asl nusxa ham o'zgaradi.

6-misol

1 - 6 + 1 2 - 2 + 1 4 - 2 3 + 1 8 - 2 9 + qatorlari yaqinlashish yoki yaqinlashmasligini hisoblang. . . va miqdorini hisoblang.

Keling, asl versiyani kengaytiramiz:

1 - 6 + 1 2 - 2 + 1 4 - 2 3 + 1 8 - 2 9 +. . . = = 1 + 1 2 + 1 4 + 1 8 +. . . - 2 · 3 + 1 + 1 3 + 1 9 +. . . = = ∑ k = 1 ∞ 1 2 k - 1 - 2 · ∑ k = 1 ∞ 1 3 k - 2

Har bir qator yaqinlashadi, chunki u sonlar qatorining a'zolaridan biridir. Uchinchi xususiyatga ko'ra, biz dastlabki versiyaning ham konvergent ekanligini hisoblashimiz mumkin. Yig'indini hisoblaymiz: qatorning birinchi hadi ∑ k = 1 ∞ 1 2 k - 1 = 1, maxraj esa = 0. 5, undan keyin, ∑ k = 1 ∞ 1 2 k - 1 = 1 1 - 0. 5 = 2. Birinchi had ∑ k = 1 ∞ 1 3 k - 2 = 3, kamayib borayotgan sonlar qatorining maxraji esa = 1 3 ga teng. Biz quyidagilarni olamiz: ∑ k = 1 ∞ 1 3 k - 2 = 3 1 - 1 3 = 9 2 .

1 - 6 + 1 2 - 2 + 1 4 - 2 3 + 1 8 - 2 9 + yig'indisini aniqlash uchun yuqorida olingan ifodalardan foydalanamiz. . . = ∑ k = 1 ∞ 1 2 k - 1 - 2 ∑ k = 1 ∞ 1 3 k - 2 = 2 - 2 9 2 = - 7

Seriyaning yaqinlashishini aniqlash uchun zaruriy shart

Ta'rif 11

Agar ∑ k = 1 ∞ a k qator yaqinlashuvchi bo'lsa, uning chegarasi kth term = 0: lim k → + ∞ a k = 0 .

Har qanday variantni tekshiradigan bo'lsak, ajralmas holat haqida unutmasligimiz kerak. Agar u bajarilmasa, seriyalar ajralib chiqadi. Agar lim k → + ∞ a k ≠ 0 bo‘lsa, qator divergent hisoblanadi.

Vaziyat muhim, ammo etarli emasligini aniqlashtirish kerak. Agar lim k → + ∞ a k = 0 tengligi bajarilsa, bu ∑ k = 1 ∞ a k ning yaqinlashuvchi ekanligini kafolatlamaydi.

Keling, misol keltiraylik. ∑ k = 1 ∞ 1 k garmonik qator uchun shart bajariladi lim k → + ∞ 1 k = 0, lekin qator baribir ajralib turadi.

7-misol

∑ n = 1 ∞ n 2 1 + n yaqinlashuvni aniqlang.

lim n → + ∞ n 2 1 + n = lim n → + ∞ n 2 n 2 1 n 2 + 1 n = lim n → + ∞ 1 1 n 2 + 1 n shartning bajarilishi uchun dastlabki ifodani tekshirib ko‘ramiz. = 1 + 0 + 0 = + ∞ ≠ 0

Cheklash nth a'zo 0 ga teng emas. Biz bu seriyaning bir-biridan farq qilishini isbotladik.

Ijobiy qatorning yaqinlashuvini qanday aniqlash mumkin.

Agar siz doimo ushbu xususiyatlardan foydalansangiz, siz doimiy ravishda chegaralarni hisoblashingiz kerak bo'ladi. Ushbu bo'lim sizga misollar va muammolarni hal qilishda qiyinchiliklardan qochishga yordam beradi. Musbat qatorning yaqinlashuvini aniqlash uchun ma'lum bir shart mavjud.

∑ k = 1 ∞ a k, a k > 0 ∀ k = 1, 2, 3, musbat belgining yaqinlashuvi uchun. . . summalarning cheklangan ketma-ketligini aniqlash kerak.

Seriyalarni qanday taqqoslash mumkin

Seriyalarni taqqoslashning bir qancha belgilari mavjud. Yaqinlashuvi aniqlanishi taklif qilingan qatorni yaqinlashuvi ma’lum bo‘lgan qatorlar bilan solishtiramiz.

Birinchi belgi

∑ k = 1 ∞ a k va ∑ k = 1 ∞ b k musbat ishorali qatorlardir. a k ≤ b k tengsizlik uchun amal qiladi k = 1, 2, 3, ... Bundan kelib chiqadiki, ∑ k = 1 ∞ b k qatordan ∑ k = 1 ∞ a k ni olishimiz mumkin. ∑ k = 1 ∞ a k divergent bo'lgani uchun ∑ k = 1 ∞ b k qatorni divergent sifatida aniqlash mumkin.

Ushbu qoida doimo tenglamalarni echish uchun ishlatiladi va yaqinlashuvni aniqlashga yordam beradigan jiddiy argumentdir. Qiyinchilik shundaki, har bir holatda taqqoslash uchun mos misolni topish mumkin emas. Ko'pincha, ketma-ketlik indikator printsipiga ko'ra tanlanadi kth had son va maxrajning darajalarini ayirish natijasiga teng bo'ladi kth seriyasining a'zosi. Faraz qilaylik, a k = k 2 + 3 4 k 2 + 5 bo‘lsa, farq teng bo‘ladi. 2 – 3 = - 1 . Bunday holda, biz seriyani taqqoslash uchun aniqlashimiz mumkin k-chi muddatli b k = k - 1 = 1 k, bu harmonikdir.

Olingan materialni birlashtirish uchun biz bir nechta odatiy variantlarni batafsil ko'rib chiqamiz.

8-misol

∑ k = 1 ∞ 1 k - 1 2 qator nima ekanligini aniqlang.

Chegara = 0 lim k → + ∞ 1 k - 1 2 = 0 bo'lgani uchun biz kerakli shartni bajardik. Tengsizlik adolatli bo'ladi 1 k< 1 k - 1 2 для k, bu tabiiydir. Oldingi paragraflardan biz ∑ k = 1 ∞ 1 k garmonik qator divergent ekanligini bilib oldik. Birinchi mezonga ko'ra, asl nusxaning farqli ekanligini isbotlash mumkin.

9-misol

Ketmalarning yaqinlashuvchi yoki divergentligini aniqlang ∑ k = 1 ∞ 1 k 3 + 3 k - 1 .

Bu misolda zarur shart bajarilgan, chunki lim k → + ∞ 1 k 3 + 3 k - 1 = 0. Biz uni 1 k 3 + 3 k - 1 tengsizlik sifatida ifodalaymiz< 1 k 3 для любого значения k. ∑ k = 1 ∞ 1 k 3 qator yaqinlashadi, chunki garmonik qator ∑ k = 1 ∞ 1 k s uchun yaqinlashadi. s > 1. Birinchi mezonga ko'ra, raqamlar qatori yaqinlashuvchi degan xulosaga kelishimiz mumkin.

10-misol

∑ k = 3 ∞ 1 k ln (ln k) qator nima ekanligini aniqlang. lim k → + ∞ 1 k ln (ln k) = 1 + ∞ + ∞ = 0.

Ushbu parametrda siz kerakli shartning bajarilishini belgilashingiz mumkin. Taqqoslash uchun qatorni belgilaymiz. Masalan, ∑ k = 1 ∞ 1 k s. Darajaning nima ekanligini aniqlash uchun ketma-ketlikni ko'rib chiqing (ln (ln k)), k = 3, 4, 5. . . . Ketma-ket a'zolar ln (ln 3) , ln (ln 4) , ln (ln 5) , . . . cheksizgacha ortadi. Tenglamani tahlil qilib, shuni ta'kidlashimiz mumkinki, qiymat sifatida N = 1619, keyin ketma-ketlik shartlari > 2 ga teng. Bu ketma-ketlik uchun 1 k ln (ln k) tengsizlik to'g'ri bo'ladi< 1 k 2 . Ряд ∑ k = N ∞ 1 k 2 сходится согласно первому признаку, так как ряд ∑ k = 1 ∞ 1 k 2 тоже сходящийся. Отметим, что согласно первому признаку ряд ∑ k = N ∞ 1 k ln (ln k) сходящийся. Можно сделать вывод, что ряд ∑ k = 3 ∞ 1 k ln (ln k) также сходящийся.

Ikkinchi belgi

∑ k = 1 ∞ a k va ∑ k = 1 ∞ b k musbat sonlar qatori deb faraz qilaylik.

Agar lim k → + ∞ a k b k ≠ ∞ bo‘lsa, u holda ∑ k = 1 ∞ b k qator yaqinlashadi va ∑ k = 1 ∞ a k ham yaqinlashadi.

Agar lim k → + ∞ a k b k ≠ 0 bo‘lsa, u holda ∑ k = 1 ∞ b k qator ajratilganligi sababli, ∑ k = 1 ∞ a k ham ayirboshlanadi.

Agar lim k → + ∞ a k b k ≠ ∞ va lim k → + ∞ a k b k ≠ 0 bo‘lsa, qatorning yaqinlashuvi yoki divergensiyasi boshqasining yaqinlashishi yoki divergentsiyasini bildiradi.

∑ k = 1 ∞ 1 k 3 + 3 k - 1 ni ikkinchi belgi yordamida ko'rib chiqing. Taqqoslash uchun ∑ k = 1 ∞ b k ∑ k = 1 ∞ 1 k 3 yaqinlashuvchi qatorni olamiz. Limitni aniqlaymiz: lim k → + ∞ a k b k = lim k → + ∞ 1 k 3 + 3 k - 1 1 k 3 = lim k → + ∞ k 3 k 3 + 3 k - 1 = 1

Ikkinchi mezonga ko'ra, ∑ k = 1 ∞ 1 k 3 yaqinlashuvchi qator asl nusxaning ham yaqinlashishini bildirishini aniqlash mumkin.

11-misol

∑ n = 1 ∞ k 2 + 3 4 k 3 + 5 qator nima ekanligini aniqlang.

Ushbu versiyada qanoatlantiriladigan lim k → ∞ k 2 + 3 4 k 3 + 5 = 0 zarur shartni tahlil qilaylik. Ikkinchi mezonga ko'ra, ∑ k = 1 ∞ 1 k qatorni oling. Biz chegarani qidiramiz: lim k → + ∞ k 2 + 3 4 k 3 + 5 1 k = lim k → + ∞ k 3 + 3 k 4 k 3 + 5 = 1 4

Yuqoridagi tezislarga ko'ra, divergent qator asl qatorning divergentsiyasini keltirib chiqaradi.

Uchinchi belgi

Taqqoslashning uchinchi belgisini ko'rib chiqaylik.

∑ k = 1 ∞ a k va _ ∑ k = 1 ∞ b k musbat son qator deb faraz qilaylik. Agar ma'lum a k + 1 a k ≤ b k + 1 b k uchun shart bajarilsa, bu qatorning yaqinlashuvi ∑ k = 1 ∞ b k ∑ k = 1 ∞ a k qator ham yaqinlashuvchi ekanligini bildiradi. Divergent qator ∑ k = 1 ∞ a k divergentsiyani ∑ k = 1 ∞ b k.

D'Alembert belgisi

Tasavvur qilaylik, ∑ k = 1 ∞ a k musbat sonlar qatori. Agar lim k → + ∞ a k + 1 a k bo‘lsa< 1 , то ряд является сходящимся, если lim k → + ∞ a k + 1 a k >1, keyin divergent.

Eslatma 1

Agar chegara cheksiz bo'lsa, D'Alember testi haqiqiydir.

Agar lim k → + ∞ a k + 1 a k = - ∞ bo‘lsa, qator yaqinlashuvchi, agar lim k → ∞ a k + 1 a k = + ∞ bo‘lsa, u divergent hisoblanadi.

Agar lim k → + ∞ a k + 1 a k = 1 bo‘lsa, u holda d'Alember belgisi yordam bermaydi va yana bir qancha tadqiqotlar talab etiladi.

12-misol

D’Alember mezoni yordamida qator yaqinlashuvchi yoki divergent ∑ k = 1 ∞ 2 k + 1 2 k ekanligini aniqlang.

Kerakli yaqinlashuv sharti bajarilganligini tekshirish kerak. Limitni L'Hopital qoidasi yordamida hisoblaymiz: lim k → + ∞ 2 k + 1 2 k = ∞ ∞ = lim k → + ∞ 2 k + 1 " 2 k " = lim k → + ∞ 2 2 k ln 2 = 2 + ∞ ln 2 = 0

Shart bajarilganligini ko'rishimiz mumkin. D'Alember testidan foydalanamiz: lim k → + ∞ = lim k → + ∞ 2 (k + 1) + 1 2 k + 1 2 k + 1 2 k = 1 2 lim k → + ∞ 2 k + 3 2 k + 1 = 12< 1

Seriya konvergent hisoblanadi.

13-misol

Qatlamning divergent ∑ k = 1 ∞ k k k ekanligini aniqlang! .

Qatorning divergensiyasini aniqlash uchun d'Alember testidan foydalanamiz: lim k → + ∞ a k + 1 a k = lim k → + ∞ (k + 1) k + 1 (k + 1) ! k k k! = lim k → + ∞ (k + 1) k + 1 · k ! k k · (k + 1) ! = lim k → + ∞ (k + 1) k + 1 k k · (k + 1) = = lim k → + ∞ (k + 1) k k k = lim k → + ∞ k + 1 k k = lim k → + ∞ 1 + 1 k k = e > 1

Shuning uchun seriyalar bir-biridan farq qiladi.

Radikal Koshi belgisi

∑ k = 1 ∞ a k musbat ishorali qator deb faraz qilaylik. Agar lim k → + ∞ a k k bo‘lsa< 1 , то ряд является сходящимся, если lim k → + ∞ a k k >1, keyin divergent.

Eslatma 2

Agar lim k → + ∞ a k k = 1 bo'lsa, bu belgi hech qanday ma'lumot bermaydi - qo'shimcha tahlil talab qilinadi.

Bu xususiyatni aniqlash oson bo'lgan misollarda foydalanish mumkin. Raqamlar qatorining a'zosi ko'rsatkichli daraja ifodasi bo'lsa, holat odatiy bo'ladi.

Qabul qilingan ma'lumotlarni birlashtirish uchun bir nechta tipik misollarni ko'rib chiqaylik.

14-misol

∑ k = 1 ∞ 1 (2 k + 1) k musbat ishorali qator yaqinlashuvchi yoki yo‘qligini aniqlang.

Kerakli shart bajarilgan deb hisoblanadi, chunki lim k → + ∞ 1 (2 k + 1) k = 1 + ∞ + ∞ = 0.

Yuqorida muhokama qilingan mezonga ko'ra, biz lim k → + ∞ a k k = lim k → + ∞ 1 (2 k + 1) k k = lim k → + ∞ 1 2 k + 1 = 0 ni olamiz.< 1 . Данный ряд является сходимым.

15-misol

∑ k = 1 ∞ 1 3 k · 1 + 1 k k 2 sonlar qatori yaqinlashadimi?

Biz oldingi bandda tasvirlangan xususiyatdan foydalanamiz lim k → + ∞ 1 3 k 1 + 1 k k 2 k = 1 3 lim k → + ∞ 1 + 1 k k = e 3< 1 , следовательно, числовой ряд сходится.

Integral Koshi testi

∑ k = 1 ∞ a k musbat ishorali qator deb faraz qilaylik. Uzluksiz argument funktsiyasini belgilash kerak y = f(x), bu n = f (n) bilan mos keladi. Agar y = f(x) noldan katta, uzilmaydi va [ a ga kamayadi; + ∞) , bu erda a ≥ 1

U holda, agar ∫ a + ∞ f (x) d x noto'g'ri integrali yaqinlashuvchi bo'lsa, ko'rib chiqilayotgan qator ham yaqinlashadi. Agar u farqlansa, ko'rib chiqilayotgan misolda qator ham ajralib chiqadi.

Funksiyaning kamayib borayotganini tekshirishda oldingi darslarda o‘tilgan materialdan foydalanishingiz mumkin.

16-misol

Konvergentsiya uchun ∑ k = 2 ∞ 1 k · ln k misolini ko'rib chiqing.

lim k → + ∞ 1 k · ln k = 1 + ∞ = 0 bo'lgani uchun qatorning yaqinlashuv sharti bajarilgan deb hisoblanadi. y = 1 x ln x deb hisoblaymiz. U noldan katta, uzilmaydi va [ 2 ga kamayadi; + ∞) . Birinchi ikki nuqta aniq ma'lum, ammo uchinchisini batafsilroq muhokama qilish kerak. Hosilani toping: y " = 1 x · ln x " = x · ln x " x · ln x 2 = ln x + x · 1 x x · ln x 2 = - ln x + 1 x · ln x 2. Bu noldan kichik [ 2 ; + ∞).Bu funksiya kamayib borayotgan tezisni isbotlaydi.

Aslida, y = 1 x ln x funktsiyasi biz yuqorida ko'rib chiqilgan printsipning xususiyatlariga mos keladi. Undan foydalanamiz: ∫ 2 + ∞ d x x · ln x = lim A → + ∞ ∫ 2 A d (ln x) ln x = lim A → + ∞ ln (ln x) 2 A = = lim A → + ∞ (ln) ( ln A) - ln (ln 2)) = ln (ln (+ ∞)) - ln (ln 2) = + ∞

Olingan natijalarga ko'ra, asl misol farqlanadi, chunki noto'g'ri integral divergent hisoblanadi.

17-misol

∑ k = 1 ∞ 1 (10 k - 9) (ln (5 k + 8)) 3 qatorning yaqinlashuvini isbotlang.

lim k → + ∞ 1 (10 k - 9) (ln (5 k + 8)) 3 = 1 + ∞ = 0 bo'lgani uchun shart bajarilgan deb hisoblanadi.

k = 4 dan boshlab, to'g'ri ifoda 1 (10 k - 9) (ln (5 k + 8)) 3< 1 (5 k + 8) (ln (5 k + 8)) 3 .

Agar ∑ k = 4 ∞ 1 (5 k + 8) (ln (5 k + 8)) 3 qator yaqinlashuvchi deb hisoblansa, u holda taqqoslash tamoyillaridan biriga ko'ra, ∑ k = 4 ∞ 1 (10) qatorga teng bo'ladi. k - 9) ( ln (5 k + 8)) 3 ham yaqinlashuvchi hisoblanadi. Shu tarzda biz asl ifodaning ham konvergent ekanligini aniqlashimiz mumkin.

Isbotga o'tamiz: ∑ k = 4 ∞ 1 (5 k + 8) (ln (5 k + 8)) 3 .

y = 1 5 x + 8 (ln (5 x + 8)) 3 funksiya noldan katta bo lgani uchun u uzilmaydi va [ 4 ga kamayadi; + ∞) . Biz oldingi paragrafda tasvirlangan xususiyatdan foydalanamiz:

∫ 4 + ∞ d x (5 x + 8) (l n (5 x + 8)) 3 = lim A → + ∞ ∫ 4 A d x (5 x + 8) (ln (5 x + 8)) 3 = = 1 5 lim A → + ∞ ∫ 4 A d (ln (5 x + 8) (ln (5 x + 8)) 3 = - 1 10 lim A → + ∞ 1 (ln (5 x + 8)) 2 | 4 A = = - 1 10 lim A → + ∞ 1 (ln (5 A + 8)) 2 - 1 (ln (5 4 + 8)) 2 = = - 1 10 1 + ∞ - 1 (ln 28) 2 = 1 10 · ln 28 2

Olingan konvergent qatorda ∫ 4 + ∞ d x (5 x + 8) (ln (5 x + 8)) 3, ∑ k = 4 ∞ 1 (5 k + 8) (ln (5 k +) ekanligini aniqlashimiz mumkin. 8 )) 3 ham yaqinlashadi.

Raabe belgisi

∑ k = 1 ∞ a k musbat sonlar qatori deb faraz qilaylik.

Agar lim k → + ∞ k · a k a k + 1 bo‘lsa< 1 , то ряд расходится, если lim k → + ∞ k · a k a k + 1 - 1 >1, keyin u birlashadi.

Agar yuqorida tavsiflangan usullar ko'rinadigan natijalarni bermasa, ushbu aniqlash usulidan foydalanish mumkin.

Mutlaq konvergentsiyani o'rganish

Tadqiqot uchun ∑ k = 1 ∞ b k ni olamiz. Biz ∑ k = 1 ∞ b k musbat belgidan foydalanamiz. Biz yuqorida tavsiflangan har qanday mos xususiyatlardan foydalanishimiz mumkin. Agar ∑ k = 1 ∞ b k qator yaqinlashsa, asl qator absolyut yaqinlashadi.

18-misol

∑ k = 1 ∞ (- 1) k 3 k 3 + 2 k - 1 qatorni yaqinlashuv uchun ∑ k = 1 ∞ (- 1) k 3 k 3 + 2 k - 1 = ∑ k = 1 ∞ 1 3 k qatorini o‘rganing. 3 + 2 k - 1.

Shart bajariladi lim k → + ∞ 1 3 k 3 + 2 k - 1 = 1 + ∞ = 0 . Biz ∑ k = 1 ∞ 1 k 3 2 dan foydalanamiz va ikkinchi belgidan foydalanamiz: lim k → + ∞ 1 3 k 3 + 2 k - 1 1 k 3 2 = 1 3 .

∑ k = 1 ∞ (- 1) k 3 k 3 + 2 k - 1 qator yaqinlashadi. Asl seriya ham mutlaqo konvergentdir.

O'zgaruvchan qatorlarning divergentsiyasi

Agar ∑ k = 1 ∞ b k qator divergent bo'lsa, u holda mos keladigan o'zgaruvchan qator ∑ k = 1 ∞ b k yo divergent yoki shartli yaqinlashuvchi bo'ladi.

∑ k = 1 ∞ b k modullaridan ajralishdan ∑ k = 1 ∞ b k haqida xulosa chiqarishga faqat d'Alember testi va radikal Koshi testi yordam beradi. ∑ k = 1 ∞ b k qator ham zarur yaqinlashuv sharti bajarilmasa, ya'ni lim k → ∞ + b k ≠ 0 bo'lsa, ajralib chiqadi.

19-misol

Divergensiyani tekshirish 1 7, 2 7 2, - 6 7 3, 24 7 4, 120 7 5 - 720 7 6,. . . .

Modul kth atama b k = k shaklida ifodalanadi! 7 k.

∑ k = 1 ∞ b k = ∑ k = 1 ∞ k qatorni tekshiramiz! d'Alember testi yordamida yaqinlashish uchun 7 k: lim k → + ∞ b k + 1 b k = lim k → + ∞ (k + 1) ! 7 k + 1 k! 7 k = 1 7 · lim k → + ∞ (k + 1) = + ∞ .

∑ k = 1 ∞ b k = ∑ k = 1 ∞ k! 7 k asl nusxadagi kabi farqlanadi.

20-misol

∑ k = 1 ∞ (- 1) k · k 2 + 1 ln (k + 1) konvergent hisoblanadi.

Kerakli shartni ko'rib chiqamiz lim k → + ∞ b k = lim k → + ∞ k 2 + 1 ln (k + 1) = ∞ ∞ = lim k → + ∞ = k 2 + 1 " (ln (k + 1)) " = = lim k → + ∞ 2 k 1 k + 1 = lim k → + ∞ 2 k (k + 1) = + ∞ . Shart bajarilmagan, shuning uchun ∑ k = 1 ∞ (- 1) k · k 2 + 1 ln (k + 1) qator farqlanadi. Limit L'Hopital qoidasi yordamida hisoblab chiqilgan.

Shartli yaqinlashish mezonlari

Leybnits testi

Ta'rif 12

Agar o'zgaruvchan qator shartlarining qiymatlari kamaysa b 1 > b 2 > b 3 > . . . > . . . va modul chegarasi = 0 sifatida k → + ∞, keyin ∑ k = 1 ∞ b k qator yaqinlashadi.

17-misol

Konvergentsiya uchun ∑ k = 1 ∞ (- 1) k 2 k + 1 5 k (k + 1) ni hisobga oling.

Seriya ∑ k = 1 ∞ (- 1) k 2 k + 1 5 k (k + 1) = ∑ k = 1 ∞ 2 k + 1 5 k (k + 1) shaklida ifodalanadi. Kerakli shart bajariladi: lim k → + ∞ = 2 k + 1 5 k (k + 1) = 0 . lim k → + ∞ 2 k + 1 5 k (k + 1) 1 k = lim k → + ∞ 2 k + 1 5 (k + 1) = 2 5 ikkinchi taqqoslash mezoni bo‘yicha ∑ k = 1 ∞ 1 k ni ko‘rib chiqaylik.

∑ k = 1 ∞ (- 1) k 2 k + 1 5 k (k + 1) = ∑ k = 1 ∞ 2 k + 1 5 k (k + 1) farqlanishini topamiz. ∑ k = 1 ∞ (- 1) k 2 k + 1 5 k (k + 1) qatori Leybnits mezoniga muvofiq yaqinlashadi: ketma-ketlik 2 1 + 1 5 1 1 1 + 1 = 3 10, 2 2 + 1 5 2 (2 + 1) = 5 30, 2 3 + 1 5 3 3 + 1, . . . kamayadi va lim k → + ∞ = 2 k + 1 5 k (k + 1) = 0 bo'ladi.

Seriya shartli ravishda yaqinlashadi.

Abel-Dirichlet testi

Ta'rif 13

∑ k = 1 + ∞ u k · v k yaqinlashadi, agar ( u k ) oshmasa va ∑ k = 1 + ∞ v k ketma-ketlik chegaralangan bo'lsa.

17-misol

1 - 3 2 + 2 3 + 1 4 - 3 5 + 1 3 + 1 7 - 3 8 + 2 9 + ni o'rganing. . . konvergentsiya uchun.

Tasavvur qilaylik

1 - 3 2 + 2 3 + 1 4 - 3 5 + 1 3 + 1 7 - 3 8 + 2 9 +. . . = 1 1 + 1 2 (- 3) + 1 3 2 + 1 4 1 + 1 5 (- 3) + 1 6 = ∑ k = 1 ∞ u k v k

Bu erda (u k) = 1, 1 2, 1 3, . . . ortib bormaydi va ketma-ketlik (v k) = 1, - 3, 2, 1, - 3, 2,. . . cheklangan (S k) = 1, - 2, 0, 1, - 2, 0,. . . . Seriya birlashadi.

Agar siz matnda xatolikni sezsangiz, uni belgilang va Ctrl+Enter tugmalarini bosing

Sonlar qatorining ta’rifi va uning yaqinlashuvi.

Konvergentsiyaning zaruriy belgisi

Cheksiz sonlar ketma-ketligi bo'lsin.

Ta'rif. Ifoda

, (1)

yoki, bir xil narsa nima deyiladi raqamlar seriyasi, va raqamlar https://pandia.ru/text/79/302/images/image005_146.gif" width="53" height="31"> – seriya a'zolari. Ixtiyoriy raqamga ega bo'lgan a'zo chaqiriladin-m, yoki seriyaning umumiy a'zosi.

O'z-o'zidan (1) ifoda o'ziga xos sonli ma'noga ega emas, chunki yig'indini hisoblashda har safar biz faqat cheklangan sonli atamalar bilan ishlaymiz. Bu iboraning ma'nosini quyidagicha aniqlash tabiiydir.

(1) qator berilsin.

Ta'rif. so'mnseriyaning birinchi a'zolari

chaqirdi n th qisman miqdor qator. Keling, qisman yig'indilar ketma-ketligini tuzamiz:

font-size:14.0pt">Cheksiz sonni oshirish bilannjami qator a'zolarining ortib borayotgan sonini hisobga oladi. Shuning uchun bunday ta'rifni berish maqsadga muvofiqdir.

Ta'rif. Agar qisman yig'indilar ketma-ketligining cheklangan chegarasi mavjud bo'lsa https://pandia.ru/text/79/302/images/image011_76.gif" width="103" height="41"> u deyiladi. miqdori.

Agar ketma-ketlik https://pandia.ru/text/79/302/images/image013_77.gif" width="80" height="31"> bo'lsa, 2) o'zgaruvchan bo'lsa.Har ikki holatda ham shunday deyishadi. seriyada hech qanday summa yo'q.

1-misol. Geometrik progressiyaning hadlaridan tashkil topgan qatorni ko'rib chiqing:

, (2)

bu yerda – progressiyaning birinchi hadi deb ataladi va font-size:14.0pt"> font-size:14.0pt">font-size:14.0pt">Bu yerdan: bu qatorning qisman yigʻindisi:

1) agar , keyin

font-size:14.0pt">ya'ni, geometrik progressiyalar qatori yaqinlashadi va uning yig'indisi .

Xususan, agar , qator uning yig'indisi ham yaqinlashadi.

Qachon https://pandia.ru/text/79/302/images/image026_42.gif" width="307" height="59 src="> uning yig'indisi ham yaqinlashadi.

2) agar , keyin , ya'ni (2) qator ajraladi.

3) agar , u holda (2) qator font-size:14.0pt"> shaklini oladi va, ya'ni qatorlar ajralib chiqadi(shrift o'lchamida: 18.0pt">).

4) agar https://pandia.ru/text/79/302/images/image036_32.gif" width="265" height="37">. Ushbu qator uchun

https://pandia.ru/text/79/302/images/image038_28.gif" width="253" height="31 src=">,

ya'ni.gif" eni="67" balandligi="41"> mavjud emas, shuning uchun qatorlar ham ajralib chiqadi(da ) .

Toʻgʻridan-toʻgʻri qator yigʻindisini hisoblash, taʼrifi boʻyicha, qisman yigʻindilarni aniq hisoblash font-size:14.0pt"> va ularning ketma-ketligi chegarasini topish qiyinligi tufayli juda noqulay. Lekin, agar qator yaqinlashayotganligi aniqlansa, uning summasini taxminan hisoblash mumkin, chunki ketma-ketlikning chegarasini aniqlashdan kelib chiqadiki, etarlicha katta. Shuning uchun, seriyalarni o'rganishda bu etarli

1) qatorning yig‘indisini topmasdan turib yaqinlashuvini aytish imkonini beruvchi texnikani bilish;

2) aniqlay olishfont-size:14.0pt">.gif" width="16 height=24" height="24"> ma'lum bir aniqlik bilan.

Sonlar qatorlarining yaqinlashuvi konvergentsiya testlari deb ataladigan teoremalar yordamida aniqlanadi.

Majburiy belgi konvergentsiya

Agar qator yaqinlashsa, uning umumiy atamasi nolga intiladi, ya'ni font-size:14.0pt">.gif" width="61 height=63" height="63"> diverges.

2-misol. Bu qatorni isbotlang 0 " style="border-collapse:collapse">

;

;

;

.

Yechim.

A) https://pandia.ru/text/79/302/images/image051_28.gif" width="176" height="81 src="> farqlanadi.

va shuning uchun qator farqlanadi. Eritmada ikkinchi ajoyib ishlatilgan

chegara: (tafsilotlarga qarang).

B) shrift-size:14.0pt">, ya'ni ketma-ketlik

- cheksiz

kichik Font-size bilan beri:14.0pt">~ (qarang), keyin ~ .

Buni hisobga olsak, biz quyidagilarni olamiz:

Bu ketma-ketlik ajralishini anglatadi.

D) shrift o'lchami: 14.0pt">,

shuning uchun qatorlar ajralib chiqadi.

Vaziyat hisoblanadi zarur, Lekin yetarli emas qatorning yaqinlashish sharti: ular uchun ko'plab qatorlar mavjud, lekin shunga qaramay bir-biridan farq qiladi.

3-misol. Font-size:14.0pt"> qatorining yaqinlashuvini oʻrganing Yechim. e'tibor bering, bu https://pandia.ru/text/79/302/images/image066_20.gif" width="119" height="59 src="> , ya'ni yaqinlashuvning zarur sharti qondiriladi. Qisman miqdor

chapga">

- bir marta

shuning uchun font-size:14.0pt">, ya'ni seriya ta'rifi bo'yicha farqlanadi.

Musbat qatorlar yaqinlashuvining yetarli belgilari

Mayli. Keyin seriyafont-size:14.0pt"> Taqqoslash belgisi

Mayli va ijobiy belgili qatorlardir. Agar tengsizlik hamma uchun qanoatlantirilsa, qatorning yaqinlashuvidan qatorning yaqinlashuvi, ketma-ketlikning divergentsiyasidan esa https://pandia.ru/text/79/302/images/image074_19.gif" kengligi kelib chiqadi. "55" balandligi "60">.

Agar https://pandia.ru/text/79/302/images/image072_18.gif" width="60" height="24"> tengsizlik bo'lsa, bu belgi o'z kuchida qoladi, lekin faqat ma'lum bir raqamdan boshlab. quyidagicha talqin qilinishi mumkin: agar kattaroq qator yaqinlashsa, kichigi yanada ko'proq yaqinlashadi; agar kichikroq qator ajralib chiqsa, kattasi ham ajralib chiqadi.

4-misol. 0 seriyaning yaqinlashuvini o'rganing " style="margin-left:50.4pt;border-collapse:collapse">

;

Yechim.

A) E'tibor bering, shrift-size:14.0pt"> hamma uchun . Umumiy a'zosi bo'lgan seriya

yaqinlashadi, chunki u maxrajli geometrik progressiya qatori (1-misolga qarang), shuning uchun bu qatortaqqoslash yo‘li bilan yaqinlashadi.

B) Qatorni ..gif" width="91" height="29 src=">.gif" width="87" height="59"> qator bilan solishtiring. diverges, demak, bu qator ham ajraladi.

Taqqoslash mezonini shakllantirishning soddaligiga qaramay, amalda uning natijasi bo'lgan quyidagi teorema qulayroqdir.

Taqqoslash chegarasi

Mayli https://pandia.ru/text/79/302/images/image071_17.gif" width="53" height="60 src="> - musbat belgilar seriyasi. Agar mavjud bo'lsa cheklangan Va nolga teng emas chegarasi, keyin ikkala qator va

bir vaqtning o'zida yaqinlashadi yoki bir vaqtning o'zida ajralib chiqadi.

Ma'lumotlar bilan taqqoslash uchun ishlatiladigan qator ko'pincha shakl qatori sifatida tanlanadi . Bunday seriya deyiladi Dirichlet yaqinida. 3 va 4-misollarda Dirixlet qatori va ajralishi ko'rsatilgan. Hozircha bu mumkin

E'tibor bering, qator font-size:14.0pt"> .

Agar bo'lsa, seriya chaqirdi garmonik. Garmonik qator ajraladi.

5-misol. Ketmalarni konvergentsiya uchun tekshiringcheklovchi taqqoslash mezonidan foydalangan holda, agar

;

;

;

Yechim. a) Chunki etarlicha katta https://pandia.ru/text/79/302/images/image101_9.gif" width="31" height="23 src="> va

~ keyin ~ font-size:14.0pt">berilgan garmonik qator bilan taqqoslash font-size:14.0pt">, ya'ni.

font-size:14.0pt"> Chegara chekli va nolga teng bo'lmaganligi sababli va garmonik qator ajralib chiqadi, bu qator ham ajralib chiqadi.

B) Etarli darajada katta https://pandia.ru/text/79/302/images/image109_10.gif" width="111" height="31 src=">.gif" width="129" height="31" uchun src=">.gif" width="132" height="64 src="> - biz buni solishtiradigan seriyaning umumiy a'zosi:

Shrift o'lchami:14.0pt">Seriallar birlashadi ( Shrift o'lchami bilan Dirichlet seriyasi: 16.0pt">), shuning uchun bu qator ham yaqinlashadi.

IN) , shuning uchun cheksiz kichik font-size:14.0pt"> mumkin

unga ekvivalent qiymat bilan almashtiring(https://pandia.ru/text/79/302/images/image058_20.gif" width="13" height="21 src="> shrift o'lchami bilan: 20.0pt">). ;

;

;

G)

;

.

1

Turi