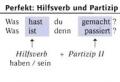
Pifagor teoremasini isbotlashning qiziqarli usullari. "Pifagor teoremasini isbotlash usullari" mavzusidagi taqdimot

Dars rejasi Tashkiliy lahza Tashkiliy nuqta Takrorlash Samoslik Pifagor hayoti haqida xabar Pifagor teoremasi haqida tarixiy ma’lumot Pifagor teoremasi haqida tarixiy ma’lumotlar Teorema ustida ishlash Teorema ustida ishlash Teoremadan foydalanib masalalar yechish. teoremadan foydalanish masalalari Darsni yakunlash Darsni yakunlash Uyga vazifa Uyga vazifa

Samoslik Pifagor Pifagor miloddan avvalgi 580 yilda tug'ilgan. Qadimgi Yunonistonda Egey dengizida Kichik Osiyo sohilida joylashgan Samos orolida, shuning uchun u Samos Pifagori deb ataladi. Boylikdan ko'ra shuhrat topgan tosh o'ymakor oilasida. Bolaligida ham u g'ayrioddiy qobiliyatlarni namoyon etdi va o'sib ulg'ayganida, yigitning notinch tasavvurlari kichik orolda tor bo'lib qoldi.

Pifagor Pifagor Milet shahriga ko'chib o'tdi va o'sha paytda sakson yoshlarda bo'lgan Thalesning shogirdi bo'ldi. Donishmand olim yigitga bir paytlar o‘zi ham ilm o‘rgangan Misrga borishni maslahat beradi. Pifagor oldida noma'lum mamlakat ochildi. Uning vatani Yunonistonda xudolar odamlar, Misr xudolari esa yarim odam – yarim hayvonlar qiyofasida bo‘lganligi uni hayratda qoldirdi. Bilimlar ma'badlarda to'plangan, ularga kirish cheklangan edi.

Misr ilm-fanining ko'p asrlik yutuqlari bilan tanishish uchun Pifagorga Misr madaniyatini chuqur o'rganish uchun yillar kerak bo'ldi. Pifagor Misr ruhoniylarining ilm-fanini anglab etgach, u erda o'z maktabini yaratish uchun uyiga ketdi. O'z bilimlarini ibodatxonalardan tashqariga yoyishni istamagan ruhoniylar uni qo'yib yuborishni xohlamadilar. Katta mashaqqat bilan bu to‘siqdan o‘ta oldi.

Biroq, uyga qaytayotganda, Pifagor qo'lga olindi va Bobilda tugadi. Bobilliklar aqlli odamlarni qadrlashgan, shuning uchun u Bobil donishmandlari orasida o'z o'rnini topdi. Bobil fani Misr ilmiga qaraganda ancha rivojlangan. Eng yorqin muvaffaqiyatlar algebra fanida bo'ldi.Pifagor Bobilliklar sanashda pozitsion sanoq sistemasini ixtiro qildilar va qo'lladilar, chiziqli, kvadrat va ba'zi turdagi kub tenglamalarni yecha oldilar. Pifagor Bobilda o'n yilga yaqin yashab, qirq yoshida vataniga qaytib keldi. Ammo u Samos orolida uzoq qolmadi. O'sha paytda orolni boshqargan zolim Polikratga qarshi norozilik belgisi sifatida u Krotone shahridagi Janubiy Italiyaning yunon koloniyalaridan biriga joylashdi.

U erda Pifagor aristokratiya vakillaridan yashirin yoshlar ittifoqini tuzdi. Ular uzoq sinovlardan so‘ng katta tantanalar bilan bu ittifoqqa qabul qilindi. Har bir abituriyent o‘z mulkidan voz kechib, asoschi ta’limotini sir saqlashga qasamyod qildi. Pifagorchilar, keyinchalik atalganlaridek, matematika, falsafa va tabiiy fanlarni o'rgandilar. Maktabda farmon bor edi, unga ko'ra barcha matematika ishlarining muallifligi o'qituvchiga yuklangan. Pifagor ittifoqi maxfiy edi. Ittifoqning emblemasi yoki identifikatsiya belgisi pentagram - besh qirrali yulduz edi. Pentagramga odamni yovuz ruhlardan himoya qilish qobiliyati berildi.

Pifagorchilar arifmetika va geometriyada ko'plab muhim kashfiyotlar qildilar. Ma'lumki, Pifagor shogirdlarining ma'naviy-axloqiy rivojlanishidan tashqari, ularning jismoniy rivojlanishi haqida ham qayg'urgan. Uning o‘zi nafaqat Olimpiya o‘yinlarida qatnashib, ikki marta mushtlashuvlarda g‘alaba qozongan, balki buyuk olimpiyachilar galaktikasini ham tayyorlagan.Pifagor Olim o‘zi yaratgan maktabga qirq yilga yaqin vaqt bag‘ishlagan va bir versiyaga ko‘ra, sakson yoshida. Xalq qo'zg'oloni davrida Pifagor ko'cha jangida o'ldirilgan. Uning vafotidan keyin talabalar o'z ustozlarining nomini ko'plab afsonalar bilan o'rab olishdi.

Bobil matnlarida Pifagordan 1200 yil oldin topilgan. Ko'rinishidan, uning isbotini birinchi bo'lib topgan. Shu munosabat bilan quyidagi yozuv kiritildi: "... to'g'ri burchakli uchburchakda gipotenuzaning oyoqlarga to'g'ri kelishini bilib, bug'doy xamiridan qilingan buqani qurbon qildi". Pifagor teoremasining tarixi Pifagor teoremasining tarixi qiziq. Garchi bu teorema Pifagor nomi bilan bog'liq bo'lsa-da, undan ancha oldin ma'lum bo'lgan.

Teorema To'g'ri burchakli uchburchakda gipotenuzaning kvadrati oyoqlarning kvadratlari yig'indisiga teng. Berilgan: D ABC, C = 90° Isbot: Isbot: D cos B ni hisobga olib, olamiz: (1) va (2) qo‘shsak, olamiz: cos B ni hisobga olsak, hosil bo‘ladi: SD balandligini cho‘qqidan tushiramiz. to'g'ri burchak

Slayd 2

a2+b2=c2 c a b P

Slayd 3

Pifagor to'g'ri burchakli uchburchakning bu xususiyatini kashf qilmagan, ehtimol u birinchi bo'lib uni umumlashtirgan va isbotlagan va shu bilan uni amaliyot maydonidan fan sohasiga o'tkazgan. U buni qanday qilganini bilmaymiz. Taxminlarga ko'ra, Pifagorning isboti asosiy emas, balki faqat tasdiqlash, bu xususiyatni bir qator alohida turdagi uchburchaklar bo'yicha sinovdan o'tkazish, ya'ni teng yonli to'g'ri burchakli uchburchakdan boshlab, bu aniq shakldan kelib chiqadi. 1.

Slayd 4

Slayd 5

Raqamlarning teng kattaligi tushunchasidan foydalanishga asoslangan isbotlar.

Slayd 6

Ko'rinib turibdiki, agar kvadratning maydonidan a, b oyoqlari bo'lgan to'g'ri burchakli uchburchakning maydonini to'rt baravar kamaytirsak, u holda teng maydonlar qoladi, ya'ni c2 = a2 + b2. Biroq, bu fikrga tegishli bo'lgan qadimgi hindular odatda buni yozmaganlar, balki rasmga faqat bitta so'z bilan hamrohlik qilganlar: "qarang!" Pifagor ham xuddi shunday dalil keltirgan bo'lishi mumkin.

Slayd 7

Qo'shimcha dalillar. Bu dalillar oyoqlarda qurilgan kvadratlarni gipotenuzaga qurilgan kvadrat qo'shish mumkin bo'lgan raqamlarga parchalanishiga asoslangan. Eynshteynning isboti (3-rasm) gipotenuzada qurilgan kvadratning 8 ta uchburchakka parchalanishiga asoslangan.

Slayd 8

Shaklda. 4-rasmda Pifagor teoremasining isboti Evklid elementlari bo'yicha o'rta asr Bag'dod sharhlovchisi al-Nayriziyaning bo'limidan foydalangan holda ko'rsatilgan. Bu bo'limda gipotenuzaga qurilgan kvadrat 3 ta uchburchak va 2 to'rtburchakka bo'linadi. Bu erda: ABC to'g'ri burchakli uchburchak C; DE = BF. Ushbu bo'lim yordamida teoremani isbotlang. D E

Slayd 9

To'ldirish usuli bo'yicha dalil. Bu usulning mohiyati shundan iboratki, oyoqlarda qurilgan kvadratlarga va gipotenuzada qurilgan kvadratga teng raqamlar olinadigan tarzda teng raqamlar qo'shiladi.

Slayd 10

Pifagor teoremasining haqiqiyligi AEDFPB va ACBNMQ olti burchaklarining teng kattaligidan kelib chiqadi. F

Slayd 11

Shaklda. 13 ABC – to‘rtburchak, C – to‘g‘ri burchak, CM AB, b1 – oyoq b ning gipotenuzaga proyeksiyasi, a1 – a oyog‘ining gipotenuzaga proyeksiyasi, h – gipotenuzaga chizilgan uchburchakning balandligi. ABC ACM ga o'xshash bo'lgani uchun b2 = c*b1; (1) ABC ning BCM ga o'xshashligidan a2 = c*a1 kelib chiqadi. (2) (1) va (2) tengliklarni hadlar bo'yicha qo'shib, a2 + b2 = c*b1 + c*a1 = c*(b1 + a1) = c2 ni olamiz. b

Slayd 12

15-rasmda uchta to'g'ri burchakli uchburchak trapezoidni hosil qiladi. Shuning uchun, bu raqamning maydonini to'rtburchaklar trapezoidning maydoni uchun formuladan foydalanib yoki uchta uchburchak maydonlarining yig'indisi sifatida topish mumkin. Garfildning isboti.

Slayd 13

Pifagorning tarjimai holi. Buyuk olim Pifagor miloddan avvalgi 570 yilda tug'ilgan. Samos orolida. Pifagorning otasi qimmatbaho toshlarni kesuvchi Mnesarx edi. Pifagorning onasining ismi noma'lum. Ko'pgina qadimiy guvohliklarga ko'ra, tug'ilgan bola ajoyib darajada chiroyli bo'lib, tez orada o'zining ajoyib qobiliyatlarini namoyon etdi. Yosh Pifagorlarning ustozlari orasida oqsoqol Germodamantus va Siroslik Feresidlar bor edi. Yosh Pifagorlar butun kunlarni oqsoqol Hermoning oyoqlari ostida o'tkazdilar, sitara ohangini va Gomerning olti metrlarini tingladilar. Pifagor butun umri davomida buyuk Gomer musiqasi va she'riyatiga bo'lgan ishtiyoqini saqlab qoldi. Va tan olingan donishmand bo'lib, ko'plab shogirdlar bilan o'ralgan Pifagor kunni Gomerning qo'shiqlaridan birini kuylashdan boshladi. Ferasid faylasuf boʻlib, italyan falsafa maktabining asoschisi hisoblangan. Qanday bo'lmasin, yosh Pifagorning notinch tasavvurlari juda tez orada kichkina Samosda tor bo'lib qoldi va u Miletga yo'l oldi va u erda boshqa olim - Thales bilan uchrashdi. Thales unga Pifagor qilgan bilim uchun Misrga borishni maslahat beradi. Miloddan avvalgi 548 yilda. Pifagorlar Samiya koloniyasi bo'lgan Naukratisga keldi, u erda boshpana va oziq-ovqat topish uchun kimdir bor edi.

Slayd 14

Misrliklarning tili va dinini o'rganib, Memfisga jo'nab ketadi. Fir'avnning tavsiyanomasiga qaramay, ayyor ruhoniylar Pifagorga o'zlarining sirlarini ochishga shoshilmadilar va unga qiyin sinovlarni taklif qilishdi. Ammo bilimga chanqoq Pifagor ularning barchasini engdi, garchi qazishmalarga ko'ra, Misr ruhoniylari unga ko'p narsani o'rgata olmadilar, chunki o'sha paytda Misr geometriyasi sof amaliy fan bo'lgan (o'sha davrning erni hisoblash va o'lchashga bo'lgan ehtiyojini qondiradigan). Shuning uchun, ruhoniylar unga bergan hamma narsani bilib, u ulardan qochib, Hellasdagi vataniga ko'chib o'tdi. Biroq, sayohatning bir qismini tugatgandan so'ng, Pifagor quruqlik safariga qaror qildi, bu vaqtda uni uyga ketayotgan Bobil shohi Kambis qo'lga oldi. Pifagorning Bobildagi hayotini dramatizatsiya qilishning hojati yo'q, chunki... buyuk hukmdor Kir barcha asirlarga bag'rikeng edi. Bobil matematikasi, shubhasiz, misrliklarga qaraganda ancha rivojlangan (buning misoli hisobning pozitsion tizimidir) va Pifagorning o'rganishi kerak bo'lgan ko'p narsa bor edi. Ammo miloddan avvalgi 530 yilda. Kir Oʻrta Osiyodagi qabilalarga qarshi yurish qilgan. Va shahardagi shovqin-surondan foydalanib, Pifagor o'z vataniga qochib ketdi.

Slayd 15

Va o'sha paytda Samosda zolim Polikrat hukmronlik qildi. Albatta, Pifagor saroy qulining hayotidan qoniqmadi va u Samos yaqinidagi g'orlarga nafaqaga chiqdi. Polikratning bir necha oylik da'volaridan so'ng, Pifagor Krotonga ko'chib o'tdi. Krotonda Pifagor diniy-axloqiy birodarlik yoki yashirin monastir buyrug'i ("Pifagorchilar") kabi narsalarni o'rnatdi, ularning a'zolari Pifagorcha hayot tarzini olib borishga va'da berishdi. Bu ayni paytda diniy ittifoq, siyosiy klub va ilmiy jamiyat edi. Aytish kerakki, Pifagor va'z qilgan ba'zi tamoyillar hozir ham taqlid qilishga arziydi. ...20 yil o'tdi. Birodarlikning shuhrati butun dunyoga tarqaldi. Bir kuni boy, ammo yovuz odam bo'lgan Cylon mast holda birodarlikka qo'shilishni xohlab Pifagorga keladi. Rad etishni olgach, Cylon o'z uyining o't qo'yishidan foydalanib, Pifagorga qarshi kurasha boshlaydi. Yong'in paytida Pifagoriyaliklar o'z ustozining hayotini o'zlari evaziga saqlab qolishdi, shundan keyin Pifagor xafa bo'ldi va tez orada o'z joniga qasd qildi.

Barcha slaydlarni ko'rish

Teorema tarixi. Qadimgi Xitoy Tarixiy sharhimizni qadimgi Xitoydan boshlaylik. Bu erda Chu-pei matematik kitobi alohida e'tiborni tortadi. Ushbu insho tomonlari 3, 4 va 5 bo'lgan Pifagor uchburchagi haqida gapiradi: Qadimgi Xitoydan boshlaylik. Bu erda Chu-pei matematik kitobi alohida e'tiborni tortadi. Bu asarda tomonlari 3, 4 va 5 boʻlgan Pifagor uchburchagi haqida shunday deyiladi: “Agar toʻgʻri burchak uning tarkibiy qismlariga ajralsa, uning tomonlari uchlarini bogʻlovchi chiziq 5 ga teng boʻladi, asosi 3 va balandligi boʻlsa. 4.” Xuddi shu kitobda Basharaning hind geometriyasining chizmalaridan biriga to'g'ri keladigan rasm taklif qilingan. Xuddi shu kitobda Basharaning hind geometriyasining chizmalaridan biriga to'g'ri keladigan rasm taklif qilingan.

Bobilliklar orasida Pifagor teoremasi haqida biroz ko'proq ma'lum. Xammurapi davriga, ya'ni miloddan avvalgi 2000 yilga oid bir matnda. e., to'g'ri burchakli uchburchakning gipotenuzasining taxminiy hisobi berilgan. Bundan xulosa qilishimiz mumkinki, Mesopotamiyada ular hech bo'lmaganda ba'zi hollarda to'g'ri burchakli uchburchaklar bilan hisob-kitoblarni amalga oshirishga muvaffaq bo'lishgan. Hindular orasidagi geometriya, xuddi misrliklar va bobilliklar singari, kult bilan chambarchas bog'liq edi. Ehtimol, gipotenuzaning kvadrati haqidagi teorema Hindistonda miloddan avvalgi 18-asrda allaqachon ma'lum bo'lgan. e. Qadimgi Hindiston

Kantor (eng yirik nemis matematika tarixchisi) 3² + 4² = 5² tengligi miloddan avvalgi 2300-yillarda misrliklarga ma'lum bo'lgan deb hisoblaydi. ya'ni, qirol Amenemhat I davrida (Berlin muzeyining 6619-papirusiga ko'ra) Kantorning so'zlariga ko'ra, arpedonaptlar yoki "arqon tortuvchilar" tomonlari 3, 4 va 5 bo'lgan to'g'ri burchakli uchburchaklar yordamida to'g'ri burchaklar qurgan. qurilish juda oson takrorlanishi mumkin. Keling, 12 metr uzunlikdagi arqonni olib, unga bir uchidan 3 metr, ikkinchisidan 4 metr masofada rangli chiziq bog'laymiz. To'g'ri burchak 3 va 4 metr uzunlikdagi tomonlar orasiga o'ralgan bo'ladi.

Van der Vaerden (gollandiyalik matematik) bir tomondan, Misr va Bobil matematikasi haqidagi hozirgi bilim darajasiga, ikkinchi tomondan, yunon manbalarini tanqidiy o'rganishga asoslanib, quyidagi xulosaga keldi: Fales, Pifagor va Pifagorchilar kabi birinchi yunon matematiklari matematikaning kashfiyoti emas, balki uni tizimlashtirish va asoslashdir. Ularning qo'lida noaniq g'oyalarga asoslangan hisoblash retseptlari aniq fanga aylandi ".

Buyuk olim Pifagor miloddan avvalgi 570 yilda tug'ilgan. Samos orolida. Pifagorning otasi qimmatbaho toshlarni kesuvchi Mnesarx edi. Pifagorning onasining ismi noma'lum. Ko'pgina qadimiy guvohliklarga ko'ra, tug'ilgan bola ajoyib darajada chiroyli bo'lib, tez orada o'zining ajoyib qobiliyatlarini namoyon etdi. Pifagor butun umri davomida buyuk Gomer musiqasi va she'riyatiga bo'lgan ishtiyoqini saqlab qoldi. Ko'p o'tmay, yosh Pifagorning notinch tasavvuri kichkina Samosda tor bo'ldi va u Miletga yo'l oldi va u erda boshqa olim Thales bilan uchrashdi. Keyin u sayohatga chiqadi va Bobil shohi Kir tomonidan asirga olinadi. Miloddan avvalgi 530 yilda. Kir Oʻrta Osiyodagi qabilalarga qarshi yurish qilgan. Va shahardagi shovqin-surondan foydalanib, Pifagor o'z vataniga qochib ketdi.

Va o'sha paytda Samosda zolim Polikrat hukmronlik qildi. Polikratning bir necha oylik da'volaridan so'ng, Pifagor Krotonga ko'chib o'tdi. Krotonda Pifagor diniy-axloqiy birodarlik yoki yashirin monastir ordeni ("Pifagorchilar") kabi narsalarni o'rnatdi, uning a'zolari Pifagorcha hayot tarzini olib borishga va'da berishdi.... 20 yil o'tdi. Birodarlikning shuhrati butun dunyoga tarqaldi. Bir kuni boy, ammo yovuz odam bo'lgan Cylon mast holda birodarlikka qo'shilishni xohlab Pifagorga keladi. Rad etishni olgach, Cylon o'z uyining o't qo'yishidan foydalanib, Pifagorga qarshi kurasha boshlaydi. Yong'in paytida Pifagoriyaliklar o'z ustozlarining hayotini o'zlari evaziga saqlab qolishdi, shundan keyin Pifagor xafa bo'ldi va tez orada o'z joniga qasd qildi.

Pifagor teoremasi. To'g'ri burchakli uchburchakda gipotenuzaning kvadrati oyoqlarning kvadratlari yig'indisiga teng. Teoremaning boshqa formulalari. Evklid teoremasi (so'zma-so'z tarjimasi): "To'g'ri burchakli uchburchakda to'g'ri burchakni o'rab turgan tomonning kvadrati to'g'ri burchakni o'rab turgan tomonlarning kvadratlariga tengdir". Geometria Culmonensisda (taxminan 1400) teoremaning tarjimasi shunday deyiladi: “Kvadratning uzun tomoni bo'ylab o'lchanadigan maydoni, o'ng tomonga tutashgan ikki tomoni bo'ylab o'lchangan ikkita kvadratning maydoni kabi kattadir. burchak."

Eng oddiy dalil. Teoremaning eng oddiy isboti teng yonli to'g'ri burchakli uchburchakning eng oddiy holatida olinadi. Aslida, teoremaning to'g'riligiga ishonch hosil qilish uchun teng yonli to'g'ri burchakli uchburchaklar mozaikasini ko'rib chiqish kifoya. Masalan, ABC uchburchagi uchun: AC gipotenuzasiga qurilgan kvadratda 4 ta asl uchburchaklar, yon tomonlarida qurilgan kvadratlar esa ikkitadan iborat.

Ayirish usuli bilan isbotlash. Keling, ayirish usuli yordamida boshqa dalilni ko'rib chiqaylik. Keling, Pifagor teoremasining tanish chizmasini to'rtburchaklar ramkaga kiritamiz, uning tomonlari yo'nalishlari uchburchakning oyoqlari yo'nalishlariga to'g'ri keladi. Keling, rasmda ko'rsatilgandek, to'rtburchak bir nechta uchburchak, to'rtburchak va kvadratlarga bo'lingan holda, rasmning ba'zi segmentlarini davom ettiramiz. Avval to'rtburchakdan bir nechta qismlarni olib tashlaymiz, shunda faqat gipotenuzada qurilgan kvadrat qoladi. Bu qismlar quyidagicha: 1. 1, 2, 3, 4 uchburchaklar; 2. to'rtburchak 5; 3. to'rtburchaklar 6 va kvadrat 8; 4. to'rtburchaklar 7 va kvadrat 9;

Keyin biz qismlarni to'rtburchakdan tashlaymiz, shunda faqat yon tomonlarga qurilgan kvadratchalar qoladi. Bu qismlar quyidagilar bo'ladi: 1. 6 va 7 to'rtburchaklar; 2. to'rtburchak 5; 3. to'rtburchak 1 (soyali); 4. to'rtburchak 2 (soyali); Biz qilishimiz kerak bo'lgan narsa, olib qo'yilgan qismlarning o'lchamlari teng ekanligini ko'rsatishdir. Bu raqamlarning joylashuvi tufayli ko'rish oson. Rasmdan ko'rinib turibdiki: 1. 5-to'rtburchak o'ziga kattaligi bo'yicha teng; 2. to'rtta uchburchak 1,2,3,4 o'lchamlari bo'yicha ikkita 6 va 7 to'rtburchaklarga teng; 3. 6-to'rtburchak va 8-kvadrat birgalikda olingan holda, 1-to'rtburchakga o'lchami teng (soyali); 4. 7-to'rtburchak 9-kvadrat bilan birgalikda o'lchami bo'yicha 2-to'rtburchakga teng (soyali); Teorema isbotlangan

Eynshteyn isboti E, C va F nuqtalari bir xil to'g'rida yotadi; Bu ECF burchagining daraja o'lchovining oddiy hisob-kitoblaridan kelib chiqadi (u ochilgan). CD EF ga perpendikulyar chizilgan. Gipotenuzada qurilgan kvadratning chap va o'ng tomonlari EF bilan kesishguncha yuqoriga cho'zilgan; yon EA CD bilan kesishguncha uzaytiriladi. Shunga ko'ra, teng uchburchaklar teng raqamlangan.

Haqiqatdan ham, ABD va BFC uchburchaklari ikki tomonda va ular orasidagi burchakda teng: FB = AB, BC = BD va ular orasidagi burchaklar o'zaro perpendikulyar tomonlari bo'lgan o'tmas burchaklar kabi tengdir. S ABD = 0,5 S BJLD, chunki ABD uchburchagi va BJLD to'rtburchakning umumiy asosi BD va umumiy balandligi LD. Xuddi shunday S FBC=0,5 S ABFH (BF-umumiy asos, AB-umumiy balandlik). Demak, S ABD= S FBC ekanligini hisobga olsak, bizda S BJLD= S ABFH bor. Xuddi shunday, agar siz VSK va ACE uchburchaklar tengligidan foydalanib, AE segmentini chizsangiz, S JCEL = S ACKG ekanligini isbotlaysiz. Demak, S ABFH+ S ACKG= S BJLD+ S JCEL= S BCED, bu isbotlanishi kerak bo'lgan narsa. Bu dalil Evklid tomonidan "Elementlar" asarida berilgan. Proklning (Vizantiya) yozishicha, uni Evklidning o'zi ixtiro qilgan. Evklidning isboti Elementlarning birinchi kitobining 47-bandida keltirilgan. ABC to‘g‘ri burchakli uchburchakning gipotenuzasi va oyoqlarida mos kvadratlar qurilib, BJLD to‘rtburchak ABFH kvadratiga, JCEL to‘rtburchak AGKC kvadratiga teng ekanligi isbotlangan. Keyin oyoqlardagi kvadratlar maydonlarining yig'indisi gipotenuzadagi kvadratning maydoniga teng bo'ladi.

Ikkinchi sir - Samoslik Pifagorning mashhur teoremasi isbotlarining aniq noma'lum soni. Aynan shuning uchun men sotsiologik so'rov o'tkazishga qaror qildim, bu ko'rsatdiki, keksa avlod vakillarining ko'pchiligi 250 ta dalil mavjudligiga rozi, garchi qo'shimcha manbalardan bilsam, bu teoremaning 350 dan ortiq isboti bor. nega u hatto Ginnesning rekordlar kitobiga kirgan! Lekin, albatta, bu dalillarda bir-biridan tubdan farq qiluvchi g'oyalar nisbatan kam qo'llaniladi.

Uchinchi sir shundaki, Pifagor teoremasi bugungi kunda matematikaning ramzi hisoblanadi. To'rtinchi sir - Pifagor teoremasi - bizni umumlashtirish uchun boy materiallar - aqliy faoliyatning eng muhim turi, nazariy tafakkurning asosi bo'lib, ko'plab olimlar buni biladilar. Bu erda Pifagor teoremasidan boshqa teoremalarga o'tish mumkinligini qo'shishimiz mumkin.

Beshinchi sir shundaki, ba'zi tadqiqotchilar Evklid o'zining "Elementlar" ning birinchi kitobida keltirgan dalillarni Pifagorga bog'lashadi. Boshqa tomondan, Prokl (V asr matematigi) Elementlardagi isbot Evklidning o'ziga tegishli ekanligini ta'kidladi. Biroq, bugungi kunda Pifagorni isbotlash usuli noma'lumligicha qolmoqda.

Oltinchi sir - bu teoremani birinchi bo'lib isbotlagan Pifagorning o'zi haqidagi afsona. Samoslik Pifagor o‘z teoremasini isbotlaganida, 100 ta ho‘kizni qurbon qilib, xudolarga minnatdorchilik bildirgan, degan rivoyat bor. Olimning gipnoz qobiliyati haqida ham afsonalar bor edi: go'yo u faqat bir qarash bilan qushlarning uchish yo'nalishini o'zgartira oladi. Ular, shuningdek, bu ajoyib odamni bir vaqtning o'zida turli shaharlarda ko'rishgan, ular orasida bir necha kunlik sayohatlar bo'lgan. Va u go'yoki "omad g'ildiragi" ga ega bo'lgan, uni aylantirish orqali u nafaqat kelajakni bashorat qilgan, balki kerak bo'lganda voqealar jarayoniga aralashgan.

Taqdimotning individual slaydlar bo'yicha tavsifi:

1 slayd

Slayd tavsifi:

KazGASA qoshidagi litsey o'qituvchisi Auelbekova G.U. "Pifagor teoremasi va uni isbotlashning turli usullari". 2016 yil

2 slayd

Slayd tavsifi:

MAQSAD: Asosiy maqsad Pifagor teoremasini isbotlashning turli usullarini ko'rib chiqishdir. Pifagor teoremasining fan va texnika taraqqiyotida, umuman matematikada qanday ahamiyati borligini ko‘rsating.

3 slayd

Slayd tavsifi:

Pifagorning tarjimai holidan Aholining bu hurmatli qadimgi yunoncha haqida hozir biladigan eng ko'p narsasi bitta iboraga to'g'ri keladi: "Pifagorning shimi har tomondan tengdir". Ushbu masxara mualliflari Pifagordan asrlar davomida aniq ajratilgan, aks holda ular masxara qilishga jur'at etmagan bo'lar edi. Chunki Pifagor umuman gipotenuzaning kvadrati emas, oyoqlarning kvadratlari yig'indisiga teng. Bu mashhur faylasuf. Pifagor miloddan avvalgi VI asrda yashagan, chiroyli ko'rinishga ega, uzun soqolli va boshida oltin diadema bor edi. Pifagor - bu ism emas, balki faylasuf yunon orakuli kabi doimo to'g'ri va ishonchli gapirgani uchun olgan taxallusdir. (Pifagor - "nutq bilan ishontiruvchi".) O'z nutqlari bilan u 2000 o'quvchini oldi, ular o'z oilalari bilan birgalikda Pifagor qonunlari va qoidalari amal qiladigan maktab davlatini tashkil qildilar. U birinchi bo'lib o'z ish yo'nalishiga nom berdi. "Filosof" so'zi "kosmos" so'zi kabi bizga Pifagordan kelgan. Uning falsafasida koinot ko'p. U Xudoni, insonni va tabiatni tushunish uchun algebrani geometriya, musiqa va astronomiya bilan o'rganish kerakligini ta'kidladi. Aytgancha, bu Pifagor bilimlari tizimi yunoncha "matematika" deb ataladi. Gipotenuzasi va oyoqlari bilan mashhur uchburchakka kelsak, bu, buyuk yunonning fikriga ko'ra, geometrik shakldan ham ko'proq. Bu bizning hayotimizning barcha shifrlangan hodisalarining "kalitidir". Tabiatdagi hamma narsa, dedi Pifagor, uch qismga bo'lingan. Shuning uchun har qanday masalani echishdan oldin uni uchburchak diagramma shaklida tasvirlash kerak. "Uchburchakka qarang - va muammoning uchdan ikki qismi hal qilindi."

4 slayd

Slayd tavsifi:

Endi Pifagor teoremasining uchta formulasi mavjud: 1. To'g'ri burchakli uchburchakda gipotenuzaning kvadrati oyoqlarning kvadratlari yig'indisiga teng. 2. To'g'ri burchakli uchburchakning gipotenuzasiga qurilgan kvadratning maydoni oyoqlarda qurilgan kvadratlarning maydonlarining yig'indisiga teng. 3. To'g'ri burchakli uchburchakning gipotenuzasiga qurilgan kvadrat oyoqlarda qurilgan kvadratlarga teng. Qarama-qarshi Pifagor teoremasi: a, b va c musbat sonlarning har uchligi uchun a2 + b2 = c2, a va b oyoqlari va gipotenuzasi c bo'lgan to'g'ri burchakli uchburchak mavjud. siz

5 slayd

Slayd tavsifi:

Teorema tarixidan Teorema tarixidan Rostini aytganda, teorema "Pifagor teoremasi" deb atalsa ham, Pifagorning o'zi uni kashf qilmagan. To'g'ri uchburchak va uning maxsus xususiyatlari undan ancha oldin o'rganilgan. Bu masala bo'yicha ikkita qutbli nuqtai nazar mavjud. Bir versiyaga ko'ra, Pifagor birinchi bo'lib teoremaning to'liq isbotini topdi. Boshqasiga ko'ra, dalil Pifagor muallifligiga tegishli emas. Bugun siz endi kim haq va kim nohaqligini tekshira olmaysiz. Ma'lumki, Pifagorning isboti, agar u mavjud bo'lsa, saqlanib qolmagan. Biroq, Evklid elementlarining mashhur isboti Pifagorga tegishli bo'lishi mumkinligi haqida takliflar mavjud va Evklid buni faqat qayd etgan. To'g'ri burchakli uchburchak bilan bog'liq muammolar fir'avn Amenemhat I davridagi Misr manbalarida, shoh Hammurapi hukmronligi davridagi Bobil loy lavhalarida, qadimgi hindlarning "Sulva Sutra" risolasida va qadimgi Xitoy asarida topilganligi bugungi kunda ham ma'lum. Chjou-bi suan jin”. Ko'rib turganimizdek, Pifagor teoremasi qadim zamonlardan beri matematiklarning ongini band qilgan. Buni bugungi kunda mavjud bo'lgan 500 ga yaqin turli dalillar tasdiqlaydi. Bunda boshqa hech bir teorema u bilan raqobatlasha olmaydi. Mashhur dalillar mualliflari orasida Leonardo da Vinchi va AQShning yigirmanchi prezidenti Jeyms Garfildni eslashimiz mumkin. Bularning barchasi ushbu teoremaning matematika uchun o'ta muhimligi haqida gapiradi: geometriya teoremalarining aksariyati undan olingan yoki u bilan qandaydir bog'liqdir. .

6 slayd

Slayd tavsifi:

Formulalar Teoremaning yunon, lotin va nemis tillaridan tarjima qilingan bayonotlari Evklidda bu teorema quyidagicha ifodalangan (so'zma-so'z tarjimasi): “To'g'ri burchakli uchburchakda to'g'ri burchakni o'z ichiga olgan tomonning kvadrati to'g'ri burchakni o'rab turgan tomonlardagi kvadratlarga tengdir. ”. Gerxard Klemons (12-asr boshlari) tomonidan rus tiliga tarjima qilingan arab tilidagi Annairitsi (miloddan avvalgi 900-yillar atrofida) matnining lotincha tarjimasida shunday deyilgan: “Har bir toʻgʻri burchakli uchburchakda toʻgʻri burchak ustida choʻzilgan tomondan hosil boʻlgan kvadrat tengdir. To'g'ri burchakni o'rab turgan ikki tomondan hosil bo'lgan ikkita kvadrat yig'indisi." Geometria Culmonensisda (taxminan 1400) teoremaning tarjimasi shunday deyiladi: “Kvadratning uzun tomoni bo'ylab o'lchanadigan maydoni, o'ng tomonga tutashgan ikki tomoni bo'ylab o'lchangan ikkita kvadratning maydoni kabi kattadir. burchak." F.I.Petrushevskiy tomonidan amalga oshirilgan Evklid elementlarining birinchi ruscha tarjimasida Pifagor teoremasi quyidagicha ifodalangan: “Toʻgʻri burchakli uchburchaklarda toʻgʻri burchakka qarama-qarshi tomonning kvadrati oʻng tomonni oʻz ichiga olgan tomonlar kvadratlari yigʻindisiga teng. burchak."

7 slayd

Slayd tavsifi:

Isbot uchun quyidagi konstruksiya qo‘llaniladi: to‘g‘ri burchakli to‘g‘ri burchakli uchburchak uchun oyoqlari ustidagi kvadratlar va gipotenuzaning ustidagi kvadratlar, balandlik va uni cho‘zuvchi nur yasaladi, gipotenuza ustidagi kvadratni ikkita to‘rtburchakka bo‘ladi. va. Dalil to'rtburchaklar maydonlarining oyoq ustidagi kvadrat bilan tengligini, kvadratni tashkil etuvchi ikkinchi to'rtburchakning gipotenuza va boshqa oyoq ustidagi to'rtburchaklar maydonlarining tengligini shunga o'xshash tarzda o'rnatishga qaratilgan. To'rtburchaklar maydonlarining tengligi uchburchaklarning muvofiqligi va har birining maydoni kvadratlar maydonining yarmiga teng bo'lgan va shunga mos ravishda quyidagi xususiyat bilan belgilanadi: maydon Agar raqamlar umumiy tomoniga ega bo'lsa, uchburchakning maydoni to'rtburchakning yarmiga teng bo'ladi va uchburchakning umumiy tomoniga balandligi to'rtburchakning boshqa tomoni bo'lsa. Uchburchaklarning mos kelishi ikki tomonning (kvadratlarning tomonlari) va ular orasidagi burchakning (to'g'ri burchak va burchakdan tashkil topgan) tengligidan kelib chiqadi. Shunday qilib, dalil gipotenuza ustidagi kvadratning maydonini tashkil qiladi. to'rtburchaklar soni va, oyoq ustidagi kvadratlar maydonlarining yig'indisiga teng.SODDA ISHLATI

8 slayd

Slayd tavsifi:

AJ - gipotenuzaga tushirilgan balandlik. Uning davomi gipotenuzada qurilgan kvadratni ikkita to'rtburchakka bo'lishini isbotlaylik, ularning maydonlari yon tomonlarga qurilgan tegishli Kvadratlarning maydonlariga teng. BJLD to'rtburchakning kattaligi bo'yicha ABFH kvadratiga teng ekanligini isbotlaylik. ABD=BFC uchburchak (ikki tomonda va ular orasidagi burchak BF=AB; BC=BD; burchak FBC=ABD burchagi).

Slayd 9

Slayd tavsifi:

S uchburchak ABD=1/2 S to'rtburchak BJLD, chunki ABD uchburchagi va BJLD to'rtburchaklari umumiy BD asosiga va umumiy LD balandligiga ega. SHUNDAY, S uchburchak FBC=1/2 S to'rtburchak ABFH(BF-umumiy asos, AB-umumiy balandlik). Demak, FBC uchburchakning ABD =S uchburchakning S ni hisobga olsak, bizda: S BJLD=S ABFH. SHUNDAY, BCK va ACE uchburchaklar tengligidan foydalanib, S JCEL=S ACKG ekanligi isbotlangan. S ABFH+S ACKJ=S BJLD+ S JCEL=S BCED. Uchburchak S=1/2AB x BD=1/2LD x BD=1/2 S BJLD Teorema isbotlangan. A L B D

10 slayd

Slayd tavsifi:

Hind matematigi Bxaskari a in c in a - in in c Bxaskari usulining isboti quyidagicha: gipotenuzada qurilgan kvadrat maydonini (c ²) uchburchaklar maydonlarining yig'indisi sifatida ifodalang (4S = 4· 0,5 a b) va kvadratning maydoni (a - c) ². Ya'ni, ma'lum bo'lishicha, c ² = 4 · 0,5 a b + (a – c) ² c ² = 2 a b + a ² - 2 a b + b ² c ² = a ² + b ² Teorema isbotlangan.

11 slayd

Slayd tavsifi:

Valdxaymning isboti a b c a b c Valdxaym to'g'ri burchakli uchburchakning maydoni uning oyoqlari ko'paytmasining yarmiga teng ekanligidan foydalanadi va trapezoidning maydoni uning parallel asoslari va balandligi yig'indisining yarmiga tengdir. . Endi teoremani isbotlash uchun trapetsiyaning maydonini ikki usulda ifodalash kifoya S trapetsiya = 0,5(a + b) (a + b) = 0,5 (a + b) ² S trapesiya = 0,5 a b + 0, 5 a b + 0,5 c ² O'ng tomonlarni tenglashtirib, biz 0,5 (a + b) ² = 0,5 a b + 0,5 a b + 0,5 c ² (a + b) ² = a b + a v + s ² a ² + ni olamiz 2 a v + v ² = 2 a v + s ² s ² = a ² + v ² Teorema isbotlangan.

12 slayd

Slayd tavsifi:

Xokins isboti A B C A1 B1 a c D c a c 1. C nuqtadagi markaz atrofida ∆ABC (to‘g‘ri burchakli) ni rasmda ko‘rsatilganidek, A1 B1 C pozitsiyasini egallashi uchun 90º ga aylantiramiz. 2. B1 A1 gipotenuzani A1 nuqtadan tashqarida AB chiziq bilan D nuqtada kesishguncha davom ettiramiz. B1 D segmenti ∆B1AB balandlikda bo‘ladi (chunki ∟B1DA = 90º). 3. A1AB1B to'rtburchakni ko'rib chiqaylik. Bir tomondan, SA1AV1V = SAA1 + SSSV1 =0,5v · v + 0,5a · a=0,5(a² + v²) Boshqa tomondan, SA1AV1V = SA1VV1 + SAA1V1 = 0,5 s · VD + 0,5 s · AD = = 0,5. · s ·(AD + VD) = 0,5 · s² Olingan ifodalarni tenglashtirib, 0,5 (a² + b²) = 0,5 c² a² + b² = c² ga erishamiz Teorema isbotlangan.

Slayd 13

Slayd tavsifi:

Geometrik isbot. (Goffman usuli) To‘g‘ri burchakli ABC uchburchagini qurish C. BF=CB, BFCB qurish BE=AB, BEAB qurish AD=AC, ADAC ni qurish F, C, D nuqtalari bir chiziqqa tegishli.

Slayd 14

Slayd tavsifi:

Ko'rib turganimizdek, ADFB va ACBE to'rtburchaklari o'lchamlari bo'yicha teng, chunki ABF = ECB. ADF va ACE uchburchaklari o'lchamlari bir xil. Ikkala teng to'rtburchakdan ular bo'lgan ABC uchburchagini ayirib, olamiz: 1/2a2+1/2b 2=1/2c 2 Shunga ko'ra: a2+ b 2 =c 2 Teorema isbotlangan.

15 slayd

Slayd tavsifi:

Algebraik isbot (Möhlman usuli) Berilgan to‘rtburchakning bir tomonida maydoni 0,5ab, ikkinchi tomonida 0,5pr, bu erda p uchburchakning yarim perimetri, r - chizilgan doira radiusi (r=0,5) (a+b-c)). A C

16 slayd

Slayd tavsifi:

Bizda: 0,5ab=0,5pr=0,5(a+b+c)*0,5(a+b-c) Bundan kelib chiqadiki, c2= a2+b2 Teorema isbotlangan. A C

Slayd 17

Slayd tavsifi:

Pifagor teoremasining ma'nosi Pifagor teoremasi haqli ravishda matematikaning asosiy teoremalaridan biridir. Bu teoremaning ahamiyati shundaki, uning yordami bilan geometriyadagi ko‘pgina teoremalarni olish mumkin. Zamonaviy dunyoda uning qiymati ham katta, chunki Pifagor teoremasi inson faoliyatining ko'plab sohalarida qo'llaniladi. Misol uchun, u binolarning tomlariga chaqmoqlarni o'rnatishda, muayyan me'moriy uslubdagi derazalarni ishlab chiqarishda va hatto uyali aloqa operatorlari antennalarining balandligini hisoblashda qo'llaniladi. Va bu ushbu teoremaning amaliy qo'llanilishining to'liq ro'yxati emas. Shuning uchun Pifagor teoremasini bilish va uning ma'nosini tushunish juda muhimdir.

18 slayd

Slayd tavsifi:

Adabiyotda Pifagor teoremasi. Pifagor nafaqat buyuk matematik, balki o‘z davrining buyuk mutafakkiri hamdir, keling, uning ba’zi falsafiy fikrlari bilan tanishib chiqamiz...

Slayd 19

Slayd tavsifi:

1. Tafakkur yer yuzidagi odamlar orasida hamma narsadan ustundir. 2. Don o'lchoviga o'tirmang (ya'ni, behuda yashamang). 3. Ketayotganda, orqaga qaramang (ya'ni, o'limdan oldin, hayotga yopishmang). 4. Kaltaklangan yo'ldan yurmang (ya'ni, olomonning fikriga emas, balki tushunadigan ozchilikning fikriga amal qiling). 5. Qaldirg'ochlarni uyingizda saqlamang (ya'ni, o'z tilida gapiradigan yoki o'zini tutmaydigan mehmonlarni qabul qilmang). 6. Yukni yelkaga olganlar bilan birga bo‘l, yukni tashlaganlar bilan birga bo‘lmang (ya’ni, odamlarni bekorchilikka emas, ezgulikka, mehnatga chorlang). 7. Ringda tasvir taqmang (ya'ni, xudolar haqida qanday hukm va o'ylayotganingizni odamlar oldida ko'z-ko'z qilmang).

Chernov Maksim

"Pifagor teoremasi va uni isbotlashning turli usullari" mavzusida taqdimot shaklida ishlab chiqilgan geometriya bo'yicha loyiha.

Yuklab oling:

Ko‘rib chiqish:

Taqdimotni oldindan ko‘rishdan foydalanish uchun Google hisobini yarating va unga kiring: https://accounts.google.com

Slayd sarlavhalari:

Pifagor teoremasi va uni isbotlashning turli usullari Tugallagan: Chernov Maksim 8A.

Loyihaning maqsadi: Pifagor teoremasini taqdim etish va uni isbotlashning turli usullarini taqdim etish.

Tarix Qadimgi Xitoy kitobi Chjou Bi Xuan Jing tomonlari 3, 4 va 5 bo'lgan Pifagor uchburchagi haqida gapiradi. Xuddi shu kitobda Basharaning hind geometriyasi chizmalaridan biriga to'g'ri keladigan chizma taklif etiladi. Morits Kantor (etakchi nemis matematika tarixchisi) 3² + 4² = 5² tengligi eramizdan avvalgi 2300-yillarda, qirol Amenemhat I davrida (Berlin muzeyining 6619 papirusiga ko'ra) misrliklarga ma'lum bo'lgan deb hisoblaydi. Kantorning so'zlariga ko'ra, harpedonaptlar yoki "arqon tortuvchilar" tomonlari 3, 4 va 5 bo'lgan to'g'ri burchakli uchburchaklar yordamida to'g'ri burchaklarni qurdilar. Ularning qurilish usuli juda oson takrorlanishi mumkin. Keling, 12 m uzunlikdagi arqonni olib, unga bir uchidan 3 m, ikkinchisidan 4 metr masofada rangli tasma bog'laymiz. To'g'ri burchak 3 va 4 metr uzunlikdagi tomonlar orasida bo'ladi. Harpedonaptiyaliklarga e'tiroz bildirish mumkinki, ularning qurilish usuli, masalan, barcha duradgorlar foydalanadigan yog'och kvadratdan foydalanilsa, ortiqcha bo'ladi. Darhaqiqat, Misr chizmalarida bunday asbob topilganligi ma'lum, masalan, duradgorlik ustaxonasi tasvirlangan chizmalar. Bobilliklar orasida Pifagor teoremasi haqida biroz ko'proq ma'lum. Hammurapi davriga, ya'ni miloddan avvalgi 2000 yilga oid bir matnda teng yonli to'g'ri burchakli uchburchakning gipotenuzasining taxminiy hisobi berilgan. Bundan xulosa qilishimiz mumkinki, Mesopotamiyada ular hech bo'lmaganda ba'zi hollarda to'g'ri burchakli uchburchaklar bilan hisob-kitoblarni amalga oshirishga muvaffaq bo'lishgan. Bir tomondan, Misr va Bobil matematikasi haqidagi hozirgi bilim darajasiga, ikkinchi tomondan, yunon manbalarini tanqidiy o‘rganishga asoslanib, Van der Varden (gollandiyalik matematik) teoremaning yuqori ehtimoli bor degan xulosaga keldi. Gipotenuzaning maydonida Bobilda miloddan avvalgi 18-asrda ma'lum bo'lgan. e. Proklning Evklid haqidagi sharhiga ko'ra, Pifagor (uning yillari odatda miloddan avvalgi 570-490 yillar deb hisoblanadi) Pifagor uchliklarini topish uchun algebraik usullardan foydalangan. Biroq, Prokl 410 va 485 yillar orasida yozgan. n. e. Tomas Little Heath Pifagor o'limidan 5 asr o'tgach, Pifagor teoremaning muallifi ekanligi haqida aniq ma'lumot yo'qligiga ishongan. Biroq, Plutarx va Tsitseron kabi mualliflar Pifagor teoremasi haqida yozganda, ular Pifagorning muallifligi hammaga ma'lum va shubhasiz bo'lgandek yozadilar."Bu formula shaxsan Pifagorga tegishlimi yoki yo'qmi ..., lekin biz uni ishonch bilan taxmin qilishimiz mumkin. Pifagor matematikasi davri". Afsonaga ko'ra, Pifagor o'z teoremasining kashf qilinishini katta bayram bilan nishonlagan va nishonlash uchun yuzta buqani so'ygan. Miloddan avvalgi 400 yillar atrofida. Miloddan avvalgi, Proklusga ko'ra, Platon algebra va geometriyani birlashtirgan Pifagor uchliklarini topish usulini bergan. Miloddan avvalgi 300 yillar atrofida. e. Pifagor teoremasining eng qadimgi aksiomatik isboti Evklidning elementlarida paydo bo'lgan.

Formulalar: Geometrik formulalar: Dastlab, teorema quyidagicha tuzilgan: To'g'ri burchakli uchburchakda gipotenuzada qurilgan kvadratning maydoni oyoqlarda qurilgan kvadratlar maydonlarining yig'indisiga teng. Algebraik formula: To'g'ri burchakli uchburchakda gipotenuzaning uzunligining kvadrati oyoqlarning uzunliklari kvadratlarining yig'indisiga teng. Ya'ni, uchburchakning gipotenuzasi uzunligini bilan, oyoqlari uzunliklarini a va b bilan belgilab: a2+b2=c2 Teoremaning har ikkala formulasi ham ekvivalent, lekin ikkinchi formulasi elementarroq, u talab qilmaydi. hudud tushunchasi. Ya'ni, ikkinchi bayonotni maydon haqida hech narsa bilmasdan va faqat to'g'ri burchakli uchburchakning tomonlari uzunligini o'lchash orqali tekshirish mumkin.

Isbotlar Hozirgi kunda bu teoremaning 367 ta isboti ilmiy adabiyotlarda qayd etilgan. Ehtimol, Pifagor teoremasi shunday ta'sirchan miqdordagi dalillarga ega bo'lgan yagona teoremadir. Bunday xilma-xillikni faqat teoremaning geometriya uchun fundamental ahamiyati bilan izohlash mumkin. Albatta, kontseptual jihatdan ularning barchasini oz sonli sinflarga bo'lish mumkin. Ulardan eng mashhurlari: maydon usuli bilan isbotlash, aksiomatik va ekzotik isbotlar (masalan, differentsial tenglamalar yordamida).

O'xshash uchburchaklar orqali Algebraik formulaning quyidagi isboti to'g'ridan-to'g'ri aksiomalardan tuzilgan isbotlarning eng oddiyidir. Xususan, u figuraning maydoni tushunchasidan foydalanmaydi. ABC to'g'ri burchakli C burchakli to'g'ri burchakli uchburchak bo'lsin. C dan balandlikni chizamiz va uning asosini H bilan belgilaymiz. ACH uchburchagi ikki burchakda ABC uchburchagiga o'xshaydi. Xuddi shunday, CBH uchburchagi ABC ga o'xshaydi. Belgini kiritib, biz nimaga teng Ekvivalent Qo'shishni olamiz, biz yoki isbotlashimiz kerak bo'lgan narsani olamiz

Hudud usulini qo'llagan isbotlar Quyidagi dalillar, ko'rinib turgan soddaligiga qaramay, unchalik oddiy emas. Ularning barchasi maydon xossalaridan foydalanadi, buning isboti Pifagor teoremasining o‘zini isbotlashdan murakkabroqdir.Teng to‘ldiruvchilik orqali isbotlash 1-rasmda ko‘rsatilgandek to‘rtta teng to‘g‘ri burchakli uchburchakni joylashtiramiz. Tomonlari c bo‘lgan to‘rtburchak kvadrat, chunki ikkita o'tkir burchakning yig'indisi 90 °, to'g'ri burchak esa 180 °. Butun figuraning maydoni, bir tomondan, yon tomoni (a + b) bo'lgan kvadratning maydoniga, boshqa tomondan, to'rtta uchburchakning maydonlari yig'indisiga teng. ichki kvadratning maydoni. Q.E.D. .

Evklidning isboti Evklid isbotining g'oyasi quyidagicha: keling, gipotenuzada qurilgan kvadratning yarmining yarmi oyoqlarda qurilgan kvadratlarning yarim maydonlarining yig'indisiga teng ekanligini isbotlashga harakat qilaylik, keyin esa katta va ikkita kichik kvadratlarning maydonlari teng. Keling, chap tomondagi rasmni ko'rib chiqaylik. Unda biz to'g'ri burchakli uchburchakning yon tomonlariga kvadratlar qurdik va AB gipotenuzasiga perpendikulyar bo'lgan to'g'ri burchakli C burchak cho'qqisidan s nurini chizdik, u gipotenuzaga qurilgan ABIK kvadratini ikkita to'rtburchaklar - BHJI va HAKJga kesadi, mos ravishda. Ma'lum bo'lishicha, bu to'rtburchaklar maydonlari mos keladigan oyoqlarda qurilgan kvadratlarning maydonlariga to'liq teng. Keling, DECA kvadratining maydoni AHJK to'rtburchaklar maydoniga teng ekanligini isbotlashga harakat qilaylik. Buning uchun biz yordamchi kuzatuvdan foydalanamiz: berilgan to'rtburchak bilan bir xil balandlik va asosga ega bo'lgan uchburchakning maydoni berilgan to'rtburchaklar maydonining yarmiga teng. Bu uchburchakning maydonini poydevor va balandlikning yarmi mahsuloti sifatida belgilashning natijasidir. Ushbu kuzatishdan kelib chiqadiki, ACK uchburchakning maydoni AHK uchburchagining maydoniga teng (rasmda ko'rsatilmagan), bu o'z navbatida AHJK to'rtburchaklar maydonining yarmiga teng. Keling, ACK uchburchagining maydoni ham DECA kvadratining yarmiga teng ekanligini isbotlaylik. Buning uchun qilish kerak bo'lgan yagona narsa ACK va BDA uchburchaklarining tengligini isbotlashdir (chunki BDA uchburchakning maydoni yuqoridagi xususiyatga ko'ra kvadrat maydonining yarmiga teng). Bu tenglik aniq: uchburchaklar ikkala tomonda va ular orasidagi burchakda tengdir. Ya'ni - AB=AK, AD=AC - CAK va BAD burchaklarining tengligini harakat usuli bilan isbotlash oson: biz CAK uchburchagini soat miliga teskari yo'nalishda 90° aylantiramiz, keyin ikki uchburchakning mos tomonlari o'z-o'zidan aniq bo'ladi. savol mos keladi (kvadrat tepasidagi burchak 90 ° bo'lganligi sababli). BCFG kvadrati va BHJI to'rtburchaklar maydonlarining tengligi uchun asoslar butunlay o'xshash. Shunday qilib, biz gipotenuzada qurilgan kvadratning maydoni oyoqlarda qurilgan kvadrat maydonlaridan iborat ekanligini isbotladik. Ushbu dalilning g'oyasi yuqoridagi animatsiya bilan yanada ko'proq tasvirlangan. Bu dalil "Pifagor shimlari" deb ham ataladi.

Leonardo da Vinchi isboti Isbotning asosiy elementlari simmetriya va harakatdir. Simmetriyadan ko'rinib turibdiki, chizmani ko'rib chiqaylik, segment kvadratni ikkita bir xil qismga ajratadi (chunki uchburchaklar qurilishda tengdir). Nuqta atrofida soat miliga teskari 90 graduslik aylanishdan foydalanib, biz soyali raqamlarning tengligini ko'ramiz va. Endi biz soya qilgan rasmning maydoni kichik kvadratlar (oyoqlarda qurilgan) va asl uchburchak maydonining yarmining yig'indisiga teng ekanligi aniq. Boshqa tomondan, u katta kvadrat maydonining yarmiga (gipotenuzada qurilgan) va asl uchburchakning maydoniga teng. Shunday qilib, kichik kvadratlar maydonlarining yarmi yig'indisi katta kvadratning yarmiga teng, shuning uchun oyoqlarda qurilgan kvadratlar maydonlarining yig'indisi kvadratga qurilgan kvadratning maydoniga teng. gipotenuza.

Pifagor teoremasining ma'nosi Pifagor teoremasi geometriyaning asosiy va, aytish mumkinki, eng muhim teoremalaridan biridir. Uning ahamiyati shundaki, geometriyaning aksariyat teoremalarini undan yoki uning yordami bilan chiqarish mumkin.

E'tiboringiz uchun rahmat!