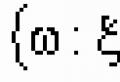Diskrēta gadījuma lieluma sadalījuma blīvums. Varbūtību sadalījuma blīvums

Jebkura nejauša eksperimenta rezultātu var raksturot kvalitatīvi un kvantitatīvi. Kvalitatīvi nejauša eksperimenta rezultāts - nejauši notikumu. Jebkurš kvantitatīvā īpašība, kas nejauša eksperimenta rezultātā var iegūt vienu no vairākām vērtībām, - nejauša vērtība. Izlases vērtība ir viens no centrālajiem varbūtības teorijas jēdzieniem.

Ļaut ir patvaļīga varbūtības telpa. Nejaušs mainīgais sauc par reālu skaitlisku funkciju x =x (w), w W tā, ka jebkuram reālam x .

Pasākums Ierasts to rakstīt formā x< x. Turpmāk nejaušie mainīgie tiks apzīmēti ar mazajiem grieķu burtiem x, h, z, ...

Nejaušais lielums ir punktu skaits, kas iegūts, metot kauliņus, vai arī no mācību grupas nejauši izvēlēta skolēna augums. Pirmajā gadījumā mums ir darīšana ar diskrēts nejaušais mainīgais(tas ņem vērtības no diskrētas skaitļu kopas M=(1, 2, 3, 4, 5, 6) ; otrajā gadījumā - ar nepārtraukts nejaušais mainīgais(tas ņem vērtības no nepārtrauktas skaitļu kopas - no skaitļu līnijas intervāla es=).

Katrs nejaušais mainīgais ir pilnībā noteikts pēc tā sadales funkcija.

Ja x ir nejaušs mainīgais, tad funkcija F(x) = Fx(x) = P(x< x) tiek saukts sadales funkcija gadījuma lielums x. Šeit P(x<x) - varbūtība, ka gadījuma lielums x iegūst vērtību, kas mazāka par x.

Ir svarīgi saprast, ka sadalījuma funkcija ir gadījuma lieluma “pase”: tā satur visu informāciju par gadījuma lielumu un tāpēc nejauša lieluma izpēte sastāv no tā izpētes izplatīšanas funkcijas, ko bieži sauc vienkārši izplatīšana.

Jebkura nejauša lieluma sadalījuma funkcijai ir šādas īpašības:

Ja x ir diskrēts gadījuma lielums, kas ņem vērtības x 1 <x 2 < … <x i < … с вероятностями lpp 1 <lpp 2 < … <p i < …, то таблица вида

x 1	x 2	…	x i	…
lpp 1	lpp 2	…	p i	…

sauca diskrēta gadījuma lieluma sadalījums.

Gadījuma lieluma sadalījuma funkcijai ar šādu sadalījumu ir forma

Diskrētam gadījuma mainīgajam ir soļu sadalījuma funkcija. Piemēram, nejaušam punktu skaitam, kas iegūts vienā metiena kauliņā, sadalījums, sadalījuma funkcija un sadalījuma funkcijas grafiks ir:

1	2	3	4	5	6
1/6	1/6	1/6	1/6	1/6	1/6

Ja sadales funkcija Fx(x) ir nepārtraukts, tad tiek izsaukts gadījuma lielums x nepārtraukts gadījuma mainīgais.

Ja nepārtraukta gadījuma lieluma sadalījuma funkcija diferencējams, tad nejaušā mainīgā vizuālāks attēlojums tiek sniegts ar nejaušā lieluma p x varbūtības blīvums(x), kas ir saistīts ar sadales funkciju Fx(x) formulas

Un .

No šejienes jo īpaši izriet, ka jebkuram nejaušam mainīgajam .

Risinot praktiskas problēmas, bieži vien ir jāatrod vērtība x, pie kuras sadales funkcija Fx(x) nejaušajam mainīgajam x ir noteikta vērtība lpp, t.i. vienādojums ir jāatrisina Fx(x) = lpp. Šāda vienādojuma risinājumi (atbilstošās vērtības x) varbūtību teorijā sauc kvantiles.

Kvantile x p ( lpp-kvantile, līmeņa kvantile lpp) gadījuma lielums ar sadalījuma funkciju Fx(x), sauc par risinājumu xp vienādojumi Fx(x) = lpp, lpp(0, 1). Dažiem lpp vienādojums Fx(x) = lpp var būt vairāki risinājumi, dažiem - neviens. Tas nozīmē, ka attiecīgajam gadījuma mainīgajam dažas kvantiles nav unikāli definētas, un dažas kvantiles neeksistē.

Pilnīga pasākumu grupa. Pretēji notikumi. Sakarība starp pretēju notikumu varbūtībām (ar secinājumu).

Atkarīgi un neatkarīgi notikumi. Pasākumu producēšana. Nosacītās varbūtības jēdziens. Varbūtību reizināšanas teorēma (ar pierādījumu).

Kopējās varbūtības un Bayes formulas (ar pierādījumu). Piemēri.

Atkārtoti neatkarīgi testi. Bernulli formula (ar secinājumu). Piemēri.

Moivre-Laplasa lokālā teorēma, tās pielietošanas nosacījumi. Funkcijas Dx īpašības). Piemērs.

Asimptotiskā Puasona formula un tās pielietošanas nosacījumi. Piemērs.

Moivre-Laplasa integrāļa teorēma un tās pielietojamības nosacījumi. Laplasa funkcija f(x) un tās īpašības. Piemērs.

Secinājumi no Moivre-Laplasa integrāļa teorēmas (ar secinājumu). Piemēri.

Diskrēta gadījuma lieluma un tā īpašību matemātiskā cerība (ar atvasinājumu). Piemēri.

Diskrēta gadījuma lieluma izkliede un tā īpašības (ar atvasināšanu). Piemēri.

Gadījuma lieluma sadalījuma funkcija, tās definīcija, īpašības un grafiks.

Nepārtraukts gadījuma mainīgais (jauns). Vienas nsv vērtības varbūtība. Matemātiskās cerības un nsv izkliede.

Nepārtraukta gadījuma lieluma varbūtības blīvums, tā definīcija, īpašības un grafiks.

Nejaušs lielums, kas sadalīts atbilstoši binomiālajam likumam, tā matemātiskajai gaidīšanai un dispersijai. Indes izplatīšanas likums.

Matemātiskā notikuma gadījumu skaita un biežuma prognoze un izkliede n atkārtotos neatkarīgos izmēģinājumos (ar secinājumiem).

Normālā sadalījuma likuma definīcija. Tā parametru teorētiskā un varbūtiskā nozīme. Normālā līkne un tās stāvokļa un formas atkarība no parametriem.

Normāli sadalīta gadījuma lieluma sadalījuma funkcija un tās izteiksme caur Laplasa funkciju.

Formulas, lai noteiktu varbūtību, ka: a) normāli sadalīts gadījuma lielums iekrīt noteiktā intervālā; b) tās novirzes no matemātiskās cerības. Trīs sigmu noteikums.

Divdimensiju (/7-dimensiju) gadījuma lieluma jēdziens. Piemēri. Tā sadalījuma tabula. Tās komponentu viendimensionālie sadalījumi. Nosacītie sadalījumi un to noteikšana pēc sadalījuma tabulas.

Gadījuma lielumu kovariance un korelācijas koeficients. Saistība starp ekorelāciju un nejaušo mainīgo neatkarību.

Divdimensiju normālā sadalījuma likuma jēdziens. Nosacītās matemātiskās cerības un dispersijas.

Markova nevienādība (Čebiševa lemma) (ar atvasinājumu). Piemērs.

Čebiševa nevienādība (ar atvasinājumu) un tās īpašie gadījumi nejaušam mainīgajam, kas sadalīts pēc binoma likuma, un notikuma biežumam.

Čebiševa teorēma (ar pierādījumu), tās nozīme un sekas. Piemērs.

Lielo skaitļu likums. Bernulli teorēma (ar pierādījumu) un tās nozīme. Piemērs.

Čebiševa nevienādība nejaušo lielumu vidējam aritmētiskajam (ar atvasinājumu).

Centrālās robežas teorēma. Ļapunova teorēmas jēdziens un tā nozīme. Piemērs.

Variāciju sērija, tās šķirnes. Vidējā aritmētiskā un rindas dispersija. Vienkāršots veids, kā tos aprēķināt.

Vispārējās populācijas parametru novērtēšanas jēdziens. Novērtējumu īpašības: objektīvs, konsekvents, efektīvs.

Vispārējās daļas novērtējums, pamatojoties uz nejaušu izlasi. Izlases proporcijas objektīvums un konsekvence.

Vispārējā vidējā aprēķins, pamatojoties uz nejaušu izlasi. Izlases vidējā objektīvums un konsekvence.

Vispārējās dispersijas novērtējums, pamatojoties uz nejaušu izlasi. Izlases dispersijas novirze un konsekvence (bez secinājuma). Izlabota izlases dispersija.

Intervālu novērtēšanas jēdziens. Pārliecības varbūtība un ticamības intervāls. Margināla izlases kļūda. Kļūdas izlases reprezentativitātē (nejaušas un sistemātiskas).

Pārliecības formula vispārējā vidējā novērtēšanai. Atkārtotu un neatkārtotu paraugu vidējā kvadrātiskā kļūda un vispārējā vidējā ticamības intervāla konstruēšana.

Nepieciešamā atkārtoto un neatkārtojamo paraugu apjoma noteikšana, novērtējot vispārējo vidējo un daļu.

Statistiskā hipotēze un statistiskais tests. 1. un 2. veida kļūdas. Testa nozīmīguma un jaudas līmenis. Praktiskās noteiktības princips.

Teorētiskā sadalījuma likuma konstruēšana, pamatojoties uz eksperimentāliem datiem. Piekrišanas kritēriju jēdziens.

X2-Pearson piemērotības kritērijs un tā piemērošanas shēma.

Funkcionālās, statistiskās un korelācijas atkarības. Atšķirības starp tām. Korelācijas teorijas galvenie uzdevumi.

Lineārā pāra regresija. Normālo vienādojumu sistēma regresijas taisnes parametru noteikšanai. Parauga kovariācija. Regresijas koeficientu aprēķināšanas formulas.

Vienkāršots veids:

Savienojuma blīvuma novērtēšana. Korelācijas koeficients (izlase), tā īpašības un ticamības novērtējums.

1. Nepārtraukta gadījuma lieluma varbūtības blīvums, tā definīcija, īpašības un grafiks.

Tiek uzskatīts, ka nejaušam mainīgajam X ir sadalījums (izplatīts) ar blīvumu
noteiktā x ass posmā. Varbūtības blīvums
, tāpat kā sadalījuma funkcija F(x), ir viena no sadalījuma likuma formām, taču atšķirībā no sadalījuma funkcijas tā pastāv tikai nepārtrauktai nejaušie mainīgie . Varbūtības blīvumu dažreiz sauc diferenciālā funkcija vai diferenciālās sadales likums . Varbūtības blīvuma diagramma
sauca sadalījuma līkne .

Nepārtraukta gadījuma lieluma varbūtības blīvuma īpašības.

☺
kā monotoni nesamazināmas funkcijas F(x) atvasinājums. ☻

☺
Saskaņā ar sadales funkcijas 4. īpašību. Tā kā F(x) ir varbūtības blīvuma antiatvasinājums
(jo
, tad saskaņā ar Ņūtona-Leibnica formulu antiatvasinājuma pieaugums segmentā [a,b] ir noteikts integrālis
. ☻

Ģeometriski iegūtā varbūtība ir vienāda ar figūras laukumu, ko augšpusē ierobežo sadalījuma līkne un balstās uz segmentu [a,b] (3.8. att.).

Nepārtraukta gadījuma lieluma sadalījuma funkciju var izteikt ar varbūtības blīvumu pēc formulas:

.

Ģeometriski sadalījuma funkcija ir vienāda ar figūras laukumu, kas robežojas virs sadalījuma līknes un atrodas pa kreisi no punkta x (3.9. att.).

Ģeometriski varbūtības blīvuma īpašības 1 un 4 nozīmē, ka tās grafiks - sadalījuma līkne - neatrodas zem abscisu ass, un attēla kopējais laukums, ko ierobežo sadalījuma līkne un abscisu ass, ir vienāds ar vienu.

1. Nejaušs lielums, kas sadalīts atbilstoši binomiālajam likumam, tā matemātiskajai gaidīšanai un dispersijai. Indes izplatīšanas likums.

Definīcija. Diskrētajam gadījuma mainīgajam X ir Binomiālā sadalījuma likums ar parametriem npq, ja tas ņem vērtības 0, 1, 2,..., m,... ,n ar varbūtībām

kur 0<р

Kā redzam, varbūtības P(X=m) tiek atrastas, izmantojot Bernulli formulu, tāpēc binomiālā sadalījuma likums ir notikuma A skaitļa X=m sadalījuma likums n neatkarīgos izmēģinājumos, kuros katrā var notikt ar tādu pašu varbūtību p .

Binoma likuma sadalījuma sērijai ir šāda forma:

Ir acīmredzams, ka binoma likuma definīcija ir pareiza, jo izplatīšanas sērijas galvenais īpašums
darīts, jo nav nekas vairāk kā visu Ņūtona binoma izvērsuma nosacījumu summa:

Paredzamā vērtība gadījuma lielums X, kas sadalīts saskaņā ar binoma likumu,

un tās dispersiju

Definīcija. Diskrētajam gadījuma mainīgajam X ir Indes izplatīšanas likums ar parametru λ > 0, ja tas ņem vērtības 0, 1, 2,..., m, ... (bezgalīga, bet saskaitāma vērtību kopa) ar varbūtībām
,

Puasona likuma izplatīšanas sērijai ir šāda forma:

Acīmredzot Puasona likuma definīcija ir pareiza, jo sadalījuma sērijas galvenā īpašība
apmierināts, jo sērijas summa.

Attēlā 4.1. attēlā parādīts pēc Puasona likuma Р(Х=m)=Р m (λ) sadalīta gadījuma lieluma sadalījuma daudzstūris (daudzstūris) ar parametriem λ = 0,5, λ = 1, λ = 2, λ = 3,5.

Teorēma. Cerības un dispersija nejauša lieluma, kas sadalīts pēc Puasona likuma, sakrīt un ir vienādi ar šī likuma parametru λ, t.i.

Un

"

Definīcija . Nepārtraukta To sauc par nejaušu mainīgo, kas var ņemt visas vērtības no kāda ierobežota vai bezgalīga intervāla.

Nepārtrauktam nejaušam mainīgajam tiek ieviests sadalījuma funkcijas jēdziens.

Definīcija. Izplatīšanas funkcija gadījuma lieluma X varbūtības ir funkcija F(x), kas katrai vērtībai x nosaka varbūtību, ka gadījuma lieluma X vērtība būs mazāka par x, tas ir:

F(x) = P(X< x)

Bieži vien termina “sadales funkcija” vietā tiek lietots termins “kumulatīvā sadalījuma funkcija”.

Sadales funkcijas īpašības:

1. Sadalījuma funkcijas vērtības pieder segmentam:

0 ≤ F(x) ≤ 1.

2. Sadales funkcija ir nesamazinoša funkcija, tas ir:

ja x > x,

tad F(x) ≥ F(x).

3. Varbūtība, ka nejaušam mainīgajam būs vērtība, kas ietverta intervālā:

varbūtība, ka nepārtraukts gadījuma mainīgais Xņems jebkuru vērtību no intervāla [ a; b], ir vienāds ar noteiktu tā varbūtības blīvuma integrāli, kas svārstās no a pirms tam b:

.

Šajā gadījumā funkcijas vispārējā formula F(x) nepārtraukta gadījuma lieluma varbūtības sadalījums, ko var izmantot, ja ir zināma blīvuma funkcija f(x) :

.

Nepārtraukta gadījuma lieluma varbūtības blīvuma grafiku sauc par tā sadalījuma līkni (attēls zemāk).

Figūras laukums (attēlā ieēnots), ko ierobežo līkne, no punktiem novilktas taisnas līnijas a Un b perpendikulāri x asij un asij Ak, grafiski parāda iespējamību, ka nepārtraukta gadījuma lieluma vērtība X atrodas diapazonā a pirms tam b.

Nepārtraukta gadījuma lieluma varbūtības blīvuma funkcijas īpašības

1. Varbūtība, ka nejaušs lielums iegūs jebkuru vērtību no intervāla (un skaitļa laukuma, ko ierobežo funkcijas grafiks f(x) un ass Ak) ir vienāds ar vienu:

2. Varbūtības blīvuma funkcijai nevar būt negatīvas vērtības:

un ārpus sadalījuma esamības tā vērtība ir nulle

Izplatības blīvums f(x), kā arī sadales funkciju F(x), ir viena no sadalījuma likuma formām, taču atšķirībā no sadalījuma funkcijas tā nav universāla: sadalījuma blīvums pastāv tikai nepārtrauktiem nejaušiem mainīgajiem.

Minēsim divus praksē svarīgākos nepārtraukta gadījuma lieluma sadalījuma veidus.

Ja sadalījuma blīvuma funkcija f(x) nepārtraukts gadījuma mainīgais kādā ierobežotā intervālā [ a; b] ņem nemainīgu vērtību C, un ārpus intervāla tiek ņemta vērtība, kas vienāda ar nulli, tad šī sadalījumu sauc par vienotu .

Ja sadalījuma blīvuma funkcijas grafiks ir simetrisks pret centru, vidējās vērtības tiek koncentrētas centra tuvumā, un, attālinoties no centra, tiek apkopotas tās, kas vairāk atšķiras no vidējā (funkcijas grafiks atgādina sadaļu no zvana), tad šis sadalījumu sauc par normālu .

1. piemērs. Nepārtraukta gadījuma lieluma varbūtības sadalījuma funkcija ir zināma:

Atrast funkciju f(x) nepārtraukta gadījuma lieluma varbūtības blīvums. Izveidojiet abu funkciju grafikus. Atrodiet varbūtību, ka nepārtraukts gadījuma mainīgais iegūs jebkuru vērtību intervālā no 4 līdz 8: .

Risinājums. Mēs iegūstam varbūtības blīvuma funkciju, atrodot varbūtības sadalījuma funkcijas atvasinājumu:

Funkcijas grafiks F(x) — parabola:

Funkcijas grafiks f(x) — taisni:

Noskaidrosim varbūtību, ka nepārtrauktam nejaušam mainīgajam būs jebkura vērtība diapazonā no 4 līdz 8:

2. piemērs. Nepārtraukta gadījuma lieluma varbūtības blīvuma funkcija ir norādīta šādi:

Aprēķināt koeficientu C. Atrast funkciju F(x) nepārtraukta gadījuma lieluma varbūtības sadalījums. Izveidojiet abu funkciju grafikus. Atrodiet varbūtību, ka nepārtrauktam nejaušam mainīgajam būs jebkura vērtība diapazonā no 0 līdz 5: .

Risinājums. Koeficients C mēs atrodam, izmantojot varbūtības blīvuma funkcijas īpašību 1:

Tādējādi nepārtraukta gadījuma lieluma varbūtības blīvuma funkcija ir:

Integrējot, mēs atrodam funkciju F(x) varbūtības sadalījumi. Ja x < 0 , то F(x) = 0. Ja 0< x < 10 , то

.

x> 10, tad F(x) = 1 .

Tādējādi pilnīgs varbūtības sadalījuma funkcijas ieraksts ir:

Funkcijas grafiks f(x) :

Funkcijas grafiks F(x) :

Noskaidrosim varbūtību, ka nepārtraukts gadījuma mainīgais iegūs jebkuru vērtību diapazonā no 0 līdz 5:

3. piemērs. Nepārtraukta gadījuma lieluma varbūtības blīvums X ir dota ar vienlīdzību , un . Atrodi koeficientu A, varbūtība, ka nepārtraukts gadījuma mainīgais Xņems jebkuru vērtību no intervāla ]0, 5[, nepārtraukta gadījuma lieluma sadalījuma funkcijas X.

Risinājums. Ar nosacījumu mēs nonākam pie vienlīdzības

Tāpēc , no kurienes . Tātad,

.

Tagad mēs atrodam varbūtību, ka nepārtraukts gadījuma mainīgais Xņems jebkuru vērtību no intervāla ]0, 5[:

Tagad mēs iegūstam šī nejaušā mainīgā sadalījuma funkciju:

4. piemērs. Atrodiet nepārtraukta gadījuma lieluma varbūtības blīvumu X, kas ņem tikai nenegatīvas vērtības, un tā sadalījuma funkciju .