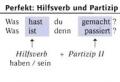
Formas interesantes de demostrar la presentación del teorema de Pitágoras. Presentación sobre el tema "métodos para demostrar el teorema de Pitágoras"

Plan de lección Momento organizacional Punto organizacional Repetición Repetición Mensaje sobre la vida de Pitágoras de Samos Mensaje sobre la vida de Pitágoras de Samos Información histórica sobre el teorema de Pitágoras Información histórica sobre el teorema de Pitágoras Trabajar en el teorema Trabajar en el teorema Resolver problemas usando el teorema Resolver problemas usando el teorema Resumiendo la lección Resumiendo la lección Tarea Tarea

Pitágoras de Samos Pitágoras nació en el año 580 a.C. en la Antigua Grecia en la isla de Samos, que se encuentra en el Mar Egeo frente a las costas de Asia Menor, por lo que se le llama Pitágoras de Samos. En la familia de un tallista de piedra que encontró fama más que riqueza. Incluso cuando era niño, mostró habilidades extraordinarias, y cuando creció, la imaginación inquieta del joven quedó limitada en la pequeña isla.

Pitágoras Pitágoras se mudó a la ciudad de Mileto y se convirtió en alumno de Tales, que en ese momento tenía más de ochenta años. El sabio científico aconsejó al joven que fuera a Egipto, donde él mismo estudió ciencias. Un país desconocido se abrió ante Pitágoras. Le llamó la atención el hecho de que en su Grecia natal los dioses tenían forma de personas y los dioses egipcios tenían forma de mitad humanos, mitad animales. El conocimiento se concentraba en los templos, cuyo acceso era limitado.

A Pitágoras le tomó años estudiar profundamente la cultura egipcia antes de que se le permitiera familiarizarse con los logros centenarios de la ciencia egipcia. Cuando Pitágoras comprendió la ciencia de los sacerdotes egipcios, regresó a su casa y creó allí su propia escuela. Los sacerdotes, que no querían difundir sus conocimientos más allá de los templos, no querían dejarlo ir. Con gran dificultad logró superar este obstáculo.

Sin embargo, de camino a casa, Pitágoras fue capturado y acabó en Babilonia. Los babilonios valoraban a las personas inteligentes, por lo que encontró su lugar entre los sabios babilónicos. La ciencia babilónica estaba más desarrollada que la ciencia egipcia. Los éxitos más sorprendentes se produjeron en álgebra. Pitágoras Los babilonios inventaron y utilizaron el sistema numérico posicional al contar y pudieron resolver ecuaciones lineales, cuadráticas y algunos tipos de ecuaciones cúbicas. Pitágoras vivió en Babilonia durante unos diez años y regresó a su tierra natal a la edad de cuarenta años. Pero no permaneció mucho tiempo en la isla de Samos. Como señal de protesta contra el tirano Polícrates, que entonces gobernaba la isla, se instaló en una de las colonias griegas del sur de Italia en la ciudad de Crotona.

Allí, Pitágoras organizó una liga secreta de jóvenes formada por representantes de la aristocracia. Fueron aceptados en esta unión con grandes ceremonias después de largas pruebas. Cada participante renunció a su propiedad y hizo un juramento de mantener en secreto las enseñanzas del fundador. Los pitagóricos, como se les llamó más tarde, estudiaron matemáticas, filosofía y ciencias naturales. En la escuela había un decreto según el cual la autoría de todos los trabajos matemáticos se atribuía al profesor. La alianza pitagórica era secreta. El emblema o marca de identificación de la unión era un pentagrama, una estrella de cinco puntas. Al pentagrama se le asignó la capacidad de proteger a una persona de los espíritus malignos.

Los pitagóricos hicieron muchos descubrimientos importantes en aritmética y geometría. También se sabe que, además del desarrollo espiritual y moral de los alumnos de Pitágoras, éste se preocupaba por su desarrollo físico. No sólo participó él mismo en los Juegos Olímpicos y ganó dos veces peleas a puñetazos, sino que también entrenó a una galaxia de grandes atletas olímpicos. Pitágoras El científico dedicó unos cuarenta años a la escuela que creó y, según una versión, a la edad de ochenta años Pitágoras murió en una pelea callejera en tiempos de levantamiento popular. Tras su muerte, los alumnos rodearon el nombre de su maestro de muchas leyendas.

En los textos babilónicos se encuentra 1200 años antes que Pitágoras. Al parecer, fue el primero en encontrar su prueba. Al respecto se hizo la siguiente entrada: “... cuando descubrió que en un triángulo rectángulo la hipotenusa corresponde a los catetos, sacrificó un toro hecho de masa de trigo”. La historia del teorema de Pitágoras La historia del teorema de Pitágoras es interesante. Aunque este teorema está asociado con el nombre de Pitágoras, se conocía mucho antes que él.

Teorema En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Dado: Δ ABC, C = 90° Demostrar: Demostración: D Considerando cos B, obtenemos: Sumando (1) y (2), obtenemos: Considerando cos B, obtenemos: Bajemos la altura SD desde el vértice de el ángulo recto

Diapositiva 2

a2+b2=c2 c a b P

Diapositiva 3

Pitágoras no descubrió esta propiedad de un triángulo rectángulo; probablemente fue el primero en generalizarla y demostrarla, transfiriéndola así del campo de la práctica al campo de la ciencia. No sabemos cómo lo hizo. Se supone que la demostración de Pitágoras no fue fundamental, sino sólo una confirmación, una prueba de esta propiedad en una serie de tipos particulares de triángulos, comenzando con un triángulo rectángulo isósceles, para lo cual se deduce obviamente de la Fig. 1.

Diapositiva 4

Diapositiva 5

Pruebas basadas en el uso del concepto de igual tamaño de figuras.

Diapositiva 6

Está claro que si restamos cuatro veces el área de un triángulo rectángulo con catetos a, b del área del cuadrado, entonces quedarán áreas iguales, es decir, c2 = a2 + b2. Sin embargo, los antiguos hindúes, a quienes pertenece este razonamiento, normalmente no lo escribían, sino que acompañaban el dibujo con una sola palabra: “¡mira!” Es muy posible que Pitágoras ofreciera la misma prueba.

Diapositiva 7

Pruebas aditivas. Estas pruebas se basan en la descomposición de cuadrados construidos sobre los catetos en figuras a las que se puede sumar un cuadrado construido sobre la hipotenusa. La prueba de Einstein (Fig. 3) se basa en la descomposición de un cuadrado construido sobre la hipotenusa en 8 triángulos.

Diapositiva 8

En la Fig. 4 muestra la demostración del teorema de Pitágoras utilizando la partición de al-Nayriziyah, el comentarista medieval de Bagdad de los Elementos de Euclides. En esta partición, el cuadrado construido sobre la hipotenusa se divide en 3 triángulos y 2 cuadriláteros. Aquí: ABC es un triángulo rectángulo con ángulo recto C; DE = BF. Demuestre el teorema usando esta partición. DE

Diapositiva 9

Evidencia por el método de cumplimentación. La esencia de este método es que se suman cifras iguales a los cuadrados construidos sobre los catetos y al cuadrado construido sobre la hipotenusa de tal manera que se obtengan cifras iguales.

Diapositiva 10

La validez del teorema de Pitágoras se deriva del mismo tamaño de los hexágonos AEDFPB y ACBNMQ. F

Diapositiva 11

En la Fig. 13 ABC – rectangular, C – ángulo recto, CM AB, b1 – proyección del cateto b sobre la hipotenusa, a1 – proyección del cateto a sobre la hipotenusa, h – altura del triángulo dibujado hasta la hipotenusa. Como ABC es similar a ACM, se deduce que b2 = c*b1; (1) del hecho de que ABC es similar a BCM, se deduce que a2 = c*a1. (2) Sumando las igualdades (1) y (2) término por término, obtenemos a2 + b2 = c*b1 + c*a1 = c*(b1 + a1) = c2. b

Diapositiva 12

En la Figura 15, tres triángulos rectángulos forman un trapezoide. Por lo tanto, el área de esta figura se puede encontrar usando la fórmula para el área de un trapezoide rectangular, o como la suma de las áreas de tres triángulos. La prueba de Garfield.

Diapositiva 13

Biografía de Pitágoras. El gran científico Pitágoras nació alrededor del año 570 a.C. en la isla de Samos. El padre de Pitágoras era Mnesarco, un tallador de gemas. Se desconoce el nombre de la madre de Pitágoras. Según muchos testimonios antiguos, el niño que nació era fabulosamente guapo y pronto mostró sus extraordinarias habilidades. Entre los maestros del joven Pitágoras se encontraban el mayor Hermodamanto y Ferécides de Siros. El joven Pitágoras pasó días enteros a los pies del mayor Hermo, escuchando la melodía de la cítara y los hexámetros de Homero. Pitágoras conservó su pasión por la música y la poesía del gran Homero durante toda su vida. Y siendo un sabio reconocido, rodeado de una multitud de discípulos, Pitágoras comenzó el día cantando una de las canciones de Homero. Ferecides fue un filósofo y fue considerado el fundador de la escuela italiana de filosofía. Pero sea como fuere, la imaginación inquieta del joven Pitágoras muy pronto quedó abarrotada en el pequeño Samos, y fue a Mileto, donde conoció a otro científico: Tales. Tales le aconseja que vaya a Egipto en busca de conocimientos, lo que hizo Pitágoras. En 548 a.C. Pitágoras llegó a Naucratis, una colonia samia, donde había alguien que podía encontrar refugio y comida.

Diapositiva 14

Después de estudiar la lengua y la religión de los egipcios, parte hacia Menfis. A pesar de la carta de recomendación del faraón, los astutos sacerdotes no tenían prisa por revelar sus secretos a Pitágoras, ofreciéndole pruebas difíciles. Pero, impulsado por la sed de conocimiento, Pitágoras los superó a todos, aunque según las excavaciones, los sacerdotes egipcios no pudieron enseñarle mucho, porque En ese momento, la geometría egipcia era una ciencia puramente aplicada (que satisfacía la necesidad de esa época de contar y medir la tierra). Por lo tanto, habiendo aprendido todo lo que le dieron los sacerdotes, se escapó de ellos y se mudó a su tierra natal en Hellas. Sin embargo, habiendo completado parte del viaje, Pitágoras decidió emprender un viaje por tierra, durante el cual fue capturado por Cambises, el rey de Babilonia, que se dirigía a casa. No es necesario dramatizar la vida de Pitágoras en Babilonia, porque... el gran gobernante Ciro fue tolerante con todos los cautivos. Sin duda, las matemáticas babilónicas estaban más desarrolladas (un ejemplo de ello es el sistema de cálculo posicional) que las egipcias, y Pitágoras tenía mucho que aprender. Pero en el 530 a.C. Ciro emprendió una campaña contra las tribus de Asia Central. Y, aprovechando la conmoción en la ciudad, Pitágoras huyó a su tierra natal.

Diapositiva 15

Y en Samos en ese momento reinaba el tirano Polícrates. Por supuesto, Pitágoras no estaba satisfecho con la vida de un esclavo de la corte y se retiró a cuevas en las cercanías de Samos. Después de varios meses de reclamos por parte de Polícrates, Pitágoras se mudó a Crotona. En Crotona, Pitágoras estableció algo así como una hermandad ético-religiosa o una orden monástica secreta (“pitagóricas”), cuyos miembros se comprometieron a llevar el llamado estilo de vida pitagórico. Era al mismo tiempo una unión religiosa, un club político y una sociedad científica. Hay que decir que algunos de los principios predicados por Pitágoras son dignos de imitación incluso ahora. ...Han pasado 20 años. La fama de la hermandad se extendió por todo el mundo. Un día, Cylon, un hombre rico pero malvado, llega a Pitágoras, queriendo unirse a la hermandad mientras está borracho. Habiendo recibido una negativa, Cylon comienza a luchar contra Pitágoras, aprovechando el incendio de su casa. Durante el incendio, los pitagóricos salvaron la vida de su maestro a costa de la suya propia, tras lo cual Pitágoras se entristeció y pronto se suicidó.

Ver todas las diapositivas

Historia del teorema. China antigua Comencemos nuestro repaso histórico por la China antigua. Aquí llama especialmente la atención el libro de matemáticas Chu-pei. Este ensayo habla sobre el triángulo pitagórico de lados 3, 4 y 5: Comencemos con la antigua China. Aquí llama especialmente la atención el libro de matemáticas Chu-pei. Esta obra dice esto sobre un triángulo pitagórico de lados 3, 4 y 5: “Si un ángulo recto se descompone en sus partes componentes, entonces la recta que une los extremos de sus lados será 5, cuando la base es 3 y la altura es 4.” En el mismo libro se propone un dibujo que coincide con uno de los dibujos de la geometría hindú de Bashara. En el mismo libro se propone un dibujo que coincide con uno de los dibujos de la geometría hindú de Bashara.

Se sabe algo más sobre el teorema de Pitágoras entre los babilonios. En un texto que se remonta a la época de Hammurabi, es decir, al año 2000 a.C. e., se da un cálculo aproximado de la hipotenusa de un triángulo rectángulo. De esto podemos concluir que en Mesopotamia se podían realizar cálculos con triángulos rectángulos, al menos en algunos casos. La geometría entre los hindúes, como entre los egipcios y los babilonios, estaba estrechamente relacionada con el culto. Es muy probable que el teorema del cuadrado de la hipotenusa ya fuera conocido en la India alrededor del siglo XVIII a.C. mi. India antigua

Cantor (el mayor historiador alemán de las matemáticas) cree que la igualdad: 3² + 4² = 5² ya era conocida por los egipcios alrededor del 2300 a.C. e., durante la época del rey Amenemhat I (según el papiro 6619 del Museo de Berlín) Según Cantor, los harpedonaptes, o “tiradores de cuerdas”, construían ángulos rectos utilizando triángulos rectángulos de lados 3, 4 y 5. Su método de La construcción se puede reproducir muy fácilmente. Tomemos una cuerda de 12 metros de largo y le atemos una franja de color a una distancia de 3 metros de un extremo y 4 metros del otro. El ángulo recto quedará encerrado entre lados de 3 y 4 metros de largo.

Basándose, por un lado, en el nivel actual de conocimientos sobre las matemáticas egipcias y babilónicas, y por otro, en un estudio crítico de las fuentes griegas, Van der Waerden (matemático holandés) llegó a la siguiente conclusión: “El mérito de la Los primeros matemáticos griegos, como Tales, Pitágoras y los pitagóricos, no es el descubrimiento de las matemáticas, sino su sistematización y justificación. En sus manos, recetas computacionales basadas en ideas vagas se convirtieron en una ciencia exacta."

El gran científico Pitágoras nació alrededor del año 570 a.C. en la isla de Samos. El padre de Pitágoras era Mnesarco, un tallador de gemas. Se desconoce el nombre de la madre de Pitágoras. Según muchos testimonios antiguos, el niño que nació era fabulosamente guapo y pronto mostró sus extraordinarias habilidades. Pitágoras conservó su pasión por la música y la poesía del gran Homero durante toda su vida. Pronto, la imaginación inquieta del joven Pitágoras quedó abarrotada en el pequeño Samos y se fue a Mileto, donde conoció a otro científico, Tales. Luego emprende un viaje y es capturado por el rey babilónico Ciro. En 530 a.C. Ciro emprendió una campaña contra las tribus de Asia Central. Y, aprovechando la conmoción en la ciudad, Pitágoras huyó a su tierra natal.

Y en Samos en ese momento reinaba el tirano Polícrates. Después de varios meses de reclamos por parte de Polícrates, Pitágoras se mudó a Crotona. En Crotona, Pitágoras estableció algo así como una hermandad ético-religiosa o una orden monástica secreta (“pitagóricos”), cuyos miembros se comprometieron a llevar el llamado estilo de vida pitagórico... Pasaron 20 años. La fama de la hermandad se extendió por todo el mundo. Un día, Cylon, un hombre rico pero malvado, llega a Pitágoras, queriendo unirse a la hermandad mientras está borracho. Habiendo recibido una negativa, Cylon comienza a luchar contra Pitágoras, aprovechando el incendio de su casa. Durante el incendio, los pitagóricos salvaron la vida de su maestro a costa de la suya propia, tras lo cual Pitágoras se entristeció y pronto se suicidó.

Teorema de pitágoras. En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Otras formulaciones del teorema. El teorema de Euclides dice (traducción literal): "En un triángulo rectángulo, el cuadrado del lado que abarca el ángulo recto es igual a los cuadrados de los lados que rodean el ángulo recto". En Geometria Culmonensis (c. 1400), la traducción del teorema dice: “El área de un cuadrado, entonces, medida a lo largo de su lado largo, es tan grande como la de dos cuadrados medidos a lo largo de sus dos lados adyacentes a un lado derecho ángulo."

La prueba más sencilla. La demostración más sencilla del teorema se obtiene en el caso más sencillo de un triángulo rectángulo isósceles. De hecho, basta con mirar el mosaico de triángulos rectángulos isósceles para convencerse de la validez del teorema. Por ejemplo, para el triángulo ABC: el cuadrado construido sobre la hipotenusa AC contiene 4 triángulos originales, y los cuadrados construidos sobre los lados contienen dos.

Prueba por método de resta. Veamos otra prueba usando el método de resta. Incluyamos el dibujo familiar del teorema de Pitágoras en un marco rectangular, cuyas direcciones de los lados coinciden con las direcciones de los catetos del triángulo. Continuamos algunos de los segmentos de la figura como se indica en la figura, mientras el rectángulo se divide en varios triángulos, rectángulos y cuadrados. Primero eliminemos varias partes del rectángulo para que solo quede el cuadrado construido sobre la hipotenusa. Estas partes son las siguientes: 1. triángulos 1, 2, 3, 4; 2. rectángulo 5; 3. rectángulo 6 y cuadrado 8; 4. rectángulo 7 y cuadrado 9;

Luego tiramos las partes del rectángulo para que solo queden los cuadrados construidos a los lados. Estas partes serán: 1. rectángulos 6 y 7; 2. rectángulo 5; 3. rectángulo 1 (sombreado); 4. rectángulo 2 (sombreado); Todo lo que tenemos que hacer es demostrar que las partes quitadas son iguales en tamaño. Esto es fácil de ver debido a la disposición de las figuras. De la figura se desprende claramente que: 1. el rectángulo 5 tiene el mismo tamaño que él mismo; 2. cuatro triángulos 1,2,3,4 tienen el mismo tamaño que dos rectángulos 6 y 7; 3. el rectángulo 6 y el cuadrado 8, tomados juntos, tienen el mismo tamaño que el rectángulo 1 (sombreado); 4. el rectángulo 7 junto con el cuadrado 9 tienen el mismo tamaño que el rectángulo 2 (sombreado); El teorema está demostrado.

La prueba de Einstein Los puntos E, C y F se encuentran en la misma recta; esto se deduce de cálculos simples de la medida en grados del ángulo ECF (está desplegado). CD se dibuja perpendicular a EF. Los lados izquierdo y derecho del cuadrado construido sobre la hipotenusa se extienden hacia arriba hasta que se cruzan con EF; El lado EA se extiende hasta que se cruza con CD. En consecuencia, los triángulos iguales tienen el mismo número.

De hecho, los triángulos ABD y BFC son iguales en dos lados y el ángulo entre ellos: FB = AB, BC = BD, y los ángulos entre ellos son iguales como ángulos obtusos con lados mutuamente perpendiculares. S ABD = 0,5 S BJLD, ya que el triángulo ABD y el rectángulo BJLD tienen una base común BD y una altura común LD. De manera similar, S FBC = 0,5 S ABFH (BF-base común, AB-altura común). Por tanto, teniendo en cuenta que S ABD= S FBC, tenemos S BJLD= S ABFH. De manera similar, si dibujas el segmento AE usando la igualdad de los triángulos ВСК y ACE, demostrarás que S JCEL = S ACKG. Entonces, S ABFH+ S ACKG= S BJLD+ S JCEL= S BCED, que es lo que había que demostrar. Esta prueba la dio Euclides en sus Elementos. Según Proclo (Bizancio), fue inventado por el propio Euclides. La prueba de Euclides se da en la frase 47 del primer libro de los Elementos. Sobre la hipotenusa y los catetos del triángulo rectángulo ABC se construyen los cuadrados correspondientes y se demuestra que el rectángulo BJLD es igual al cuadrado ABFH, y el rectángulo JCEL es igual al cuadrado AGKC. Entonces la suma de las áreas de los cuadrados de los catetos será igual al área del cuadrado de la hipotenusa.

El segundo misterio es el número exactamente desconocido de demostraciones del famoso teorema de Pitágoras de Samos. Fue por esta razón que decidí realizar una encuesta sociológica, que mostró que la mayoría de las personas de la generación mayor están de acuerdo con la existencia de 250 pruebas, aunque sé por fuentes adicionales que hay más de 350 pruebas de este teorema, que es ¡Por qué incluso entró en el Libro Guinness de los Récords! Pero, por supuesto, en estas demostraciones se utilizan relativamente pocas ideas fundamentalmente diferentes.

El tercer secreto es que el teorema de Pitágoras es un símbolo de las matemáticas actuales. El cuarto secreto, el teorema de Pitágoras, nos proporciona una gran cantidad de material para la generalización, el tipo más importante de actividad mental, la base del pensamiento teórico, que muchos científicos dominan. Aquí podemos agregar que del teorema de Pitágoras se puede pasar a otros teoremas.

El quinto secreto es que algunos investigadores atribuyen a Pitágoras la prueba que Euclides dio en el primer libro de sus Elementos. Por otro lado, Proclo (matemático del siglo V) argumentó que la prueba contenida en los Elementos pertenecía al propio Euclides. Pero aún hoy el método de prueba de Pitágoras sigue siendo desconocido.

El sexto secreto es la leyenda sobre el propio Pitágoras, el hombre que demostró por primera vez este teorema. Existe una leyenda que cuenta que cuando Pitágoras de Samos demostró su teorema, agradeció a los dioses sacrificando 100 toros. También hubo leyendas sobre las habilidades hipnóticas del científico: como si pudiera cambiar la dirección de vuelo de los pájaros con solo su mirada. También dijeron que este hombre asombroso fue visto simultáneamente en diferentes ciudades, entre las cuales hubo varios días de viaje. Y que supuestamente poseía una “rueda de la fortuna”, cuya rotación no sólo predecía el futuro, sino que también intervenía, si era necesario, en el curso de los acontecimientos.

Descripción de la presentación por diapositivas individuales:

1 diapositiva

Descripción de la diapositiva:

Profesora del Liceo de KazGASA Auelbekova G.U. "El teorema de Pitágoras y diversas formas de demostrarlo". 2016

2 diapositivas

Descripción de la diapositiva:

OBJETIVO: El objetivo principal es observar las diferentes formas de demostrar el Teorema de Pitágoras. Muestre qué importancia tiene el teorema de Pitágoras en el desarrollo de la ciencia y la tecnología, en las matemáticas en general.

3 diapositivas

Descripción de la diapositiva:

De la biografía de Pitágoras Lo máximo que la población sabe ahora sobre este respetado griego antiguo cabe en una frase: "Los pantalones de Pitágoras son iguales por todos lados". Los autores de esta burla están claramente separados por siglos de Pitágoras, de lo contrario no se habrían atrevido a bromear. Porque Pitágoras no es en absoluto el cuadrado de la hipotenusa, igual a la suma de los cuadrados de los catetos. Este es un filósofo famoso. Pitágoras vivió en el siglo VI a. C., tenía una apariencia hermosa, llevaba una larga barba y una diadema de oro en la cabeza. Pitágoras no es un nombre, sino un apodo que recibió el filósofo porque siempre hablaba de manera correcta y convincente, como un oráculo griego. (Pitágoras - "persuasivo con el habla"). Con sus discursos adquirió 2.000 estudiantes que, junto con sus familias, formaron un estado escolar, donde estaban en vigor las leyes y reglas de Pitágoras. Fue el primero en darle un nombre a su línea de trabajo. La palabra "filósofo", como la palabra "cosmos", nos llegó de Pitágoras. Hay mucho de cósmico en su filosofía. Sostuvo que para comprender a Dios, el hombre y la naturaleza, hay que estudiar álgebra con geometría, música y astronomía. Por cierto, es el sistema de conocimiento pitagórico el que en griego se llama "matemáticas". En cuanto al famoso triángulo con su hipotenusa y sus catetos, éste, según el gran griego, es más que una figura geométrica. Ésta es la "clave" de todos los fenómenos cifrados de nuestra vida. Todo en la naturaleza, decía Pitágoras, se divide en tres partes. Por tanto, antes de resolver cualquier problema, hay que representarlo en forma de diagrama triangular. "Mira el triángulo y el problema está resuelto en dos tercios".

4 diapositivas

Descripción de la diapositiva:

Ahora bien, hay tres formulaciones del teorema de Pitágoras: 1. En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. 2. El área de un cuadrado construido sobre la hipotenusa de un triángulo rectángulo es igual a la suma de las áreas de los cuadrados construidos sobre los catetos. 3. Un cuadrado construido sobre la hipotenusa de un triángulo rectángulo equivale a cuadrados construidos sobre los catetos. Teorema de Pitágoras inverso: por cada triplete de números positivos a, b y c tales que a2 + b2 = c2, existe un triángulo rectángulo con catetos a y b e hipotenusa c. tú

5 diapositiva

Descripción de la diapositiva:

De la historia del teorema De la historia del teorema Estrictamente hablando, aunque el teorema se llama "teorema de Pitágoras", el propio Pitágoras no lo descubrió. El triángulo rectángulo y sus propiedades especiales se estudiaron mucho antes que él. Hay dos puntos de vista opuestos sobre este tema. Según una versión, Pitágoras fue el primero en encontrar una demostración completa del teorema. Según otro, la prueba no pertenece a la autoría de Pitágoras. Hoy ya no se puede comprobar quién tiene razón y quién no. Lo que se sabe es que la prueba de Pitágoras, si alguna vez existió, no ha sobrevivido. Sin embargo, hay sugerencias de que la famosa prueba de los Elementos de Euclides puede pertenecer a Pitágoras, y Euclides sólo la registró. También se sabe hoy que los problemas sobre un triángulo rectángulo se encuentran en fuentes egipcias de la época del faraón Amenemhat I, en tablillas de arcilla babilónicas del reinado del rey Hammurabi, en el antiguo tratado indio "Sulva Sutra" y en la antigua obra china " Zhou-bi suan jin”. Como podemos ver, el teorema de Pitágoras ha ocupado la mente de los matemáticos desde la antigüedad. Esto lo confirman alrededor de 500 pruebas diferentes que existen en la actualidad. En esto ningún otro teorema puede competir con él. Entre los autores famosos de pruebas podemos recordar a Leonardo da Vinci y al vigésimo presidente de los Estados Unidos, James Garfield. Todo esto habla de la extrema importancia de este teorema para las matemáticas: la mayoría de los teoremas de la geometría se derivan de él o están de alguna manera relacionados con él. .

6 diapositiva

Descripción de la diapositiva:

Formulaciones Enunciados del teorema traducidos del griego, latín y alemán En Euclides, este teorema dice (traducción literal): “En un triángulo rectángulo, el cuadrado del lado que abarca el ángulo recto es igual a los cuadrados de los lados que rodean el ángulo recto .” La traducción latina del texto árabe Annairitsi (alrededor del 900 a. C.), realizada por Gerhard de Clemons (principios del siglo XII), traducida al ruso dice: “En todo triángulo rectángulo, el cuadrado formado en el lado extendido sobre el ángulo recto es igual a la suma de dos cuadrados formados por dos lados que forman un ángulo recto." En Geometria Culmonensis (c. 1400), la traducción del teorema dice: “El área de un cuadrado, entonces, medida a lo largo de su lado largo, es tan grande como la de dos cuadrados medidos a lo largo de sus dos lados adyacentes a un lado derecho ángulo." En la primera traducción rusa de los elementos euclidianos, realizada por F. I. Petrushevsky, el teorema de Pitágoras se establece de la siguiente manera: “En los triángulos rectángulos, el cuadrado del lado opuesto al ángulo recto es igual a la suma de los cuadrados de los lados que contienen el ángulo recto ángulo."

7 diapositiva

Descripción de la diapositiva:

La construcción utilizada para la demostración es la siguiente: para un triángulo rectángulo con ángulo recto, cuadrados encima de los catetos y un cuadrado encima de la hipotenusa, se construye una altura y un rayo que lo extiende, dividiendo el cuadrado encima de la hipotenusa en dos rectángulos. y. La prueba tiene como objetivo establecer la igualdad de las áreas del rectángulo con el cuadrado sobre el cateto, la igualdad de las áreas del segundo rectángulo que constituye el cuadrado con la hipotenusa y el rectángulo sobre el otro cateto de manera similar. La igualdad de las áreas de un rectángulo se establece mediante la congruencia de los triángulos y, el área de cada uno de los cuales es igual a la mitad del área de los cuadrados y, en consecuencia, en relación con la siguiente propiedad: el área del triángulo es igual a la mitad del área del rectángulo si las figuras tienen un lado común, y la altura del triángulo al lado común es el otro lado del rectángulo. La congruencia de triángulos se deriva de la igualdad de dos lados (lados de cuadrados) y el ángulo entre ellos (compuesto por un ángulo recto y un ángulo en. Así, la prueba establece que el área de un cuadrado sobre la hipotenusa, compuesta de rectángulos y, es igual a la suma de las áreas de los cuadrados encima de los catetos.PRUEBA SIMPLE

8 diapositivas

Descripción de la diapositiva:

AJ es la altura bajada a la hipotenusa. Demostremos que su continuación divide el cuadrado construido sobre la hipotenusa en dos rectángulos, cuyas áreas son iguales a las áreas de los cuadrados correspondientes construidos sobre los lados. Demostremos que el rectángulo BJLD tiene el mismo tamaño que el cuadrado ABFH. Triángulo ABD=BFC (en dos lados y el ángulo entre ellos BF=AB; BC=BD; ángulo FBC=ángulo ABD).

Diapositiva 9

Descripción de la diapositiva:

S triángulo ABD=1/2 S rectángulo BJLD, porque El triángulo ABD y el rectángulo BJLD tienen una base común BD y una altura común LD. DE MANERA SIMILAR, S triángulo FBC=1/2 S rectángulo ABFH(BF-base común, AB-altura común). Por tanto, teniendo en cuenta que S del triángulo ABD =S del triángulo FBC, tenemos: S BJLD=S ABFH. De manera similar, utilizando la igualdad de los triángulos BCK y ACE, se demuestra que S JCEL=S ACKG. S ABFH+S ACKJ=S BJLD+ S JCEL=S BCED. Triángulo S=1/2AB x BD=1/2LD x BD=1/2 S BJLD El teorema está demostrado. ALBD

10 diapositivas

Descripción de la diapositiva:

La prueba del método del matemático indio Bhaskari a in c in a - in in in c Bhaskari es la siguiente: expresa el área del cuadrado construido sobre la hipotenusa (c ²) como la suma de las áreas de los triángulos (4S = 4· 0,5 a b) y el área del cuadrado (a – c)². Es decir, resulta que c² = 4 · 0,5 a b + (a – c)² c² = 2 a b + a² - 2 a b + b² c² = a² + b² El teorema está demostrado.

11 diapositiva

Descripción de la diapositiva:

La prueba de Waldheim a b c a b c Waldheim utiliza el hecho de que el área de un triángulo rectángulo es igual a la mitad del producto de sus catetos, y el área de un trapezoide es igual al producto de la mitad de la suma de sus bases paralelas y su altura . Ahora, para demostrar el teorema, basta con expresar el área del trapezoide de dos maneras S trapezoide = 0,5(a + b) (a + b) = 0,5 (a + b)² S trapezoide = 0,5 a b + 0, 5 a b + 0,5 c ² Igualando los lados derechos, obtenemos 0,5 (a + b) ² = 0,5 a b + 0,5 a b + 0,5 c ² (a + b) ² = a b + а в + с ² а ² + 2 а в + в ² = 2 а в + с ² с ² = а ² + в ² El teorema está demostrado

12 diapositivas

Descripción de la diapositiva:

Prueba de Hawkins A B C A1 B1 a c D c a c 1. Rotemos el rectángulo ∆ABC (con ángulo recto C) alrededor del centro en el punto C 90º para que tome la posición A1 B1 C, como se muestra en la figura. 2. Continuemos la hipotenusa B1 A1 más allá del punto A1 hasta que se cruce con la recta AB en el punto D. El segmento B1 D tendrá altura ∆B1AB (ya que ∟B1DA = 90º). 3. Considere el cuadrilátero A1AB1B. Por un lado, SА1АВ1В = SАА1 + SСВВ1 =0.5в · в + 0.5а · а=0.5(а² + в²) Por otro lado, SA1АВ1В = SA1ВВ1 + SАА1В1 = 0.5 s · ВД + 0.5 s · AD = = 0.5 · s ·(AD + VD) = 0,5 · s² Igualando las expresiones resultantes obtenemos 0,5 (a² + b²) = 0,5 c² a² + b² = c² El teorema está demostrado.

Diapositiva 13

Descripción de la diapositiva:

Prueba geométrica. (Método de Hoffmann) Construir el triángulo ABC con ángulo recto C. Construir BF=CB, BFCB Construir BE=AB, BEAB Construir AD=AC, ADAC Los puntos F, C, D pertenecen a la misma recta.

Diapositiva 14

Descripción de la diapositiva:

Como vemos, los cuadriláteros ADFB y ACBE son iguales en tamaño, porque ABF=BCE. Los triángulos ADF y ACE tienen el mismo tamaño. Restamos el triángulo ABC que comparten de ambos cuadriláteros iguales, y obtenemos: 1/2a2+1/2b 2=1/2c 2 Por lo tanto: a2+ b 2 =c 2 El teorema está demostrado.

15 diapositivas

Descripción de la diapositiva:

Prueba algebraica (método de Möhlmann) El área de un rectángulo dado por un lado es 0,5ab, por el otro 0,5pr, donde p es el semiperímetro del triángulo, r es el radio del círculo inscrito (r=0,5 (a+b-c)). A C

16 diapositiva

Descripción de la diapositiva:

Tenemos: 0.5ab=0.5pr=0.5(a+b+c)*0.5(a+b-c) Se deduce que c2= a2+b2 El teorema está demostrado. A C

Diapositiva 17

Descripción de la diapositiva:

El significado del teorema de Pitágoras El teorema de Pitágoras es, con razón, uno de los principales teoremas de las matemáticas. La importancia de este teorema es que con su ayuda se pueden deducir la mayoría de los teoremas de geometría. Su valor en el mundo moderno también es grande, ya que el teorema de Pitágoras se utiliza en muchas ramas de la actividad humana. Por ejemplo, se utiliza en la colocación de pararrayos en los tejados de los edificios, en la producción de ventanas de ciertos estilos arquitectónicos e incluso en el cálculo de la altura de las antenas de los operadores de telefonía móvil. Y esta no es la lista completa de aplicaciones prácticas de este teorema. Por eso es muy importante conocer el teorema de Pitágoras y comprender su significado.

18 diapositiva

Descripción de la diapositiva:

Teorema de Pitágoras en la literatura. Pitágoras no sólo es un gran matemático, sino también un gran pensador de su tiempo. Conozcamos algunas de sus afirmaciones filosóficas...

Diapositiva 19

Descripción de la diapositiva:

1. El pensamiento está por encima de todo entre las personas de la tierra. 2. No se siente sobre una medida de grano (es decir, no viva de brazos cruzados). 3. Al partir, no mires atrás (es decir, antes de la muerte, no te aferres a la vida). 4. No sigas el camino trillado (es decir, no sigas las opiniones de la multitud, sino las opiniones de unos pocos que entienden). 5. No tengas golondrinas en tu casa (es decir, no recibas invitados que hablen o desenfrenen su idioma). 6. Esté con quienes llevan la carga, no esté con quienes la arrojan (es decir, anime a la gente no a la ociosidad, sino a la virtud, al trabajo). 7. No uses imágenes en el ring (es decir, no hagas alarde frente a la gente de cómo juzgas y piensas sobre los dioses).

Máximo de Chernov

Un proyecto sobre geometría, diseñado en forma de presentación sobre el tema "Teorema de Pitágoras y varios métodos para demostrarlo".

Descargar:

Avance:

Para utilizar vistas previas de presentaciones, cree una cuenta de Google e inicie sesión en ella: https://accounts.google.com

Títulos de diapositivas:

El teorema de Pitágoras y varios métodos para demostrarlo Completado por: Chernov Maxim 8A

Objetivo del proyecto: Presentar el teorema de Pitágoras y presentar diferentes formas de demostrarlo.

Historia El antiguo libro chino Zhou Bi Xuan Jing habla de un triángulo pitagórico de lados 3, 4 y 5. El mismo libro ofrece un dibujo que coincide con uno de los dibujos de la geometría hindú de Bashara. Moritz Cantor (el principal historiador alemán de las matemáticas) cree que la igualdad 3² + 4² = 5² ya era conocida por los egipcios alrededor del 2300 a. C., durante la época del rey Amenemhat I (según el papiro 6619 del Museo de Berlín). Según Cantor, los harpedonaptes, o “tiradores de cuerdas”, construían ángulos rectos utilizando triángulos rectángulos con lados de 3, 4 y 5. Su método de construcción se puede reproducir muy fácilmente. Tomemos una cuerda de 12 m de largo y le atemos una tira de color a una distancia de 3 m de un extremo y 4 metros del otro. El ángulo recto tendrá entre lados 3 y 4 metros de largo. A los Harpedonaptios se les podría objetar que su método de construcción se vuelve superfluo si se utiliza, por ejemplo, una escuadra de madera, que utilizan todos los carpinteros. De hecho, se conocen dibujos egipcios en los que se encuentra dicha herramienta, por ejemplo, dibujos que representan un taller de carpintería. Se sabe algo más sobre el teorema de Pitágoras entre los babilonios. Un texto que data de la época de Hammurabi, es decir, del año 2000 a.C., da un cálculo aproximado de la hipotenusa de un triángulo rectángulo isósceles. De esto podemos concluir que en Mesopotamia se podían realizar cálculos con triángulos rectángulos, al menos en algunos casos. Basándose, por un lado, en el nivel actual de conocimiento sobre las matemáticas egipcias y babilónicas, y por otro, en un estudio crítico de fuentes griegas, Van der Varden (matemático holandés) concluyó que existía una alta probabilidad de que el teorema en el cuadrado de la hipotenusa ya se conocía en Babilonia alrededor del siglo XVIII a.C. mi. Según el comentario de Proclo sobre Euclides, Pitágoras (cuyos años generalmente se consideran entre 570 y 490 a. C.) utilizó métodos algebraicos para encontrar trillizos pitagóricos. Sin embargo, Proclo escribió entre 410 y 485. norte. mi. Thomas Little Heath creía que no hay ninguna referencia explícita, que se remonta a los cinco siglos posteriores a la muerte de Pitágoras, de que Pitágoras fuera el autor del teorema. Sin embargo, cuando autores como Plutarco y Cicerón escriben sobre el teorema de Pitágoras, lo hacen como si la autoría de Pitágoras fuera ampliamente conocida e indudable: “Si esta fórmula pertenece personalmente a Pitágoras..., pero podemos asumir con confianza que pertenece a el período de las matemáticas pitagóricas." Según la leyenda, Pitágoras celebró el descubrimiento de su teorema con un banquete gigantesco, sacrificando cien toros para celebrarlo. Alrededor del 400 a.C. Antes de Cristo, según Proclo, Platón dio un método para encontrar tripletes pitagóricos, combinando álgebra y geometría. Alrededor del 300 a.C. mi. La prueba axiomática más antigua del teorema de Pitágoras apareció en los Elementos de Euclides.

Formulaciones: Formulación geométrica: Inicialmente el teorema se formuló de la siguiente manera: En un triángulo rectángulo, el área del cuadrado construido sobre la hipotenusa es igual a la suma de las áreas de los cuadrados construidos sobre los catetos. Formulación algebraica: En un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos. Es decir, denotar la longitud de la hipotenusa del triángulo por, y las longitudes de los catetos por a y b: a2+b2=c2 Ambas formulaciones del teorema son equivalentes, pero la segunda formulación es más elemental, no requiere el concepto de área. Es decir, la segunda afirmación se puede verificar sin saber nada sobre el área y midiendo sólo las longitudes de los lados de un triángulo rectángulo.

Demostraciones Actualmente, se han registrado en la literatura científica 367 demostraciones de este teorema. Probablemente el teorema de Pitágoras sea el único teorema con un número tan impresionante de demostraciones. Esta diversidad sólo puede explicarse por la importancia fundamental del teorema para la geometría. Por supuesto, conceptualmente todos ellos se pueden dividir en un pequeño número de clases. Las más famosas: pruebas por el método de áreas, pruebas axiomáticas y exóticas (por ejemplo, mediante ecuaciones diferenciales).

A través de triángulos semejantes La siguiente prueba de la formulación algebraica es la más simple de las pruebas construidas directamente a partir de los axiomas. En particular, no utiliza el concepto de área de una figura. Sea ABC un triángulo rectángulo con ángulo recto C. Dibujemos la altura de C y denotemos su base por H. El triángulo ACH es semejante al triángulo ABC en dos ángulos. Asimismo, el triángulo CBH es semejante a ABC. Introduciendo la notación obtenemos Qué es equivalente Sumando, obtenemos o, que es lo que necesitábamos demostrar

Demostraciones utilizando el método del área Las siguientes demostraciones, a pesar de su aparente simplicidad, no lo son en absoluto. Todos ellos utilizan las propiedades del área, cuya demostración es más compleja que la prueba del propio teorema de Pitágoras.Demostración mediante equicomplementariedad Dispongamos cuatro triángulos rectángulos iguales como se muestra en la Figura 1. Un cuadrilátero con lados c es un cuadrado, ya que la suma de dos ángulos agudos es 90°, y un ángulo llano es 180°. El área de toda la figura es igual, por un lado, al área de un cuadrado de lado (a + b), y por otro lado, a la suma de las áreas de los cuatro triángulos y el Área de la plaza interior. Q.E.D. .

La prueba de Euclides La idea de la prueba de Euclides es la siguiente: intentemos demostrar que la mitad del área del cuadrado construido sobre la hipotenusa es igual a la suma de las medias áreas de los cuadrados construidos sobre los catetos, y luego la las áreas de los cuadrados grande y dos pequeños son iguales. Miremos el dibujo de la izquierda. En él construimos cuadrados en los lados de un triángulo rectángulo y dibujamos un rayo s desde el vértice del ángulo recto C perpendicular a la hipotenusa AB, que corta el cuadrado ABIK, construido sobre la hipotenusa, en dos rectángulos: BHJI y HAKJ, respectivamente. Resulta que las áreas de estos rectángulos son exactamente iguales a las áreas de los cuadrados construidos sobre los catetos correspondientes. Intentemos demostrar que el área del cuadrado DECA es igual al área del rectángulo AHJK. Para hacer esto, usaremos una observación auxiliar: El área de un triángulo con la misma altura y base que el rectángulo dado es igual a la mitad del área del rectángulo dado. Esto es consecuencia de definir el área de un triángulo como la mitad del producto de la base por la altura. De esta observación se deduce que el área del triángulo ACK es igual al área del triángulo AHK (no mostrado en la figura), que a su vez es igual a la mitad del área del rectángulo AHJK. Demostremos ahora que el área del triángulo ACK también es igual a la mitad del área del cuadrado DECA. Lo único que hay que hacer para esto es demostrar la igualdad de los triángulos ACK y BDA (ya que el área del triángulo BDA es igual a la mitad del área del cuadrado según la propiedad anterior). Esta igualdad es obvia: los triángulos son iguales en ambos lados y el ángulo entre ellos. Es decir - AB=AK, AD=AC - la igualdad de los ángulos CAK y BAD es fácil de demostrar mediante el método del movimiento: rotamos el triángulo CAK 90° en el sentido contrario a las agujas del reloj, entonces es obvio que los lados correspondientes de los dos triángulos en La pregunta coincidirá (debido a que el ángulo en el vértice del cuadrado es de 90°). El razonamiento para la igualdad de las áreas del cuadrado BCFG y del rectángulo BHJI es completamente similar. Así, demostramos que el área de un cuadrado construido sobre la hipotenusa se compone de las áreas de los cuadrados construidos sobre los catetos. La idea detrás de esta prueba se ilustra con más detalle en la animación anterior. Esta prueba también se llama “pantalones pitagóricos”.

La prueba de Leonardo da Vinci Los principales elementos de la prueba son la simetría y el movimiento. Consideremos el dibujo, como se puede ver en la simetría, el segmento corta el cuadrado en dos partes idénticas (ya que los triángulos son iguales en construcción). Usando una rotación de 90 grados en sentido antihorario alrededor del punto, vemos la igualdad de las figuras sombreadas y. Ahora queda claro que el área de la figura que hemos sombreado es igual a la suma de la mitad de las áreas de los cuadrados pequeños (construidos sobre los catetos) y el área del triángulo original. Por otro lado, es igual a la mitad del área del cuadrado grande (construido sobre la hipotenusa) más el área del triángulo original. Así, la mitad de la suma de las áreas de los cuadrados pequeños es igual a la mitad del área del cuadrado grande y, por tanto, la suma de las áreas de los cuadrados construidos sobre los catetos es igual al área del cuadrado construido sobre los hipotenusa.

El significado del teorema de Pitágoras El teorema de Pitágoras es uno de los principales y, podría decirse, el más importante teorema de la geometría. Su importancia radica en el hecho de que la mayoría de los teoremas de la geometría se pueden deducir de él o con su ayuda.

¡Gracias por su atención!