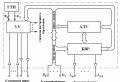
Zajímavé způsoby, jak dokázat prezentaci Pythagorovy věty. Prezentace na téma "metody dokazování Pythagorovy věty"
Plán lekce Organizační moment Organizační moment Opakování Zpráva o životě Pythagora ze Samosu Zpráva o životě Pythagora ze Samos Historické pozadí Pythagorovy věty Historické pozadí Pythagorovy věty Práce na větě Práce na větě Řešení problémů pomocí věty Řešení problémy s použitím věty Shrnutí hodiny Shrnutí hodiny domácí úkol domácí úkol



Pythagoras Pythagoras ze Samosu se narodil v roce 580 před naším letopočtem. ve starověkém Řecku na ostrově Samos, který se nachází v Egejském moři u pobřeží Malé Asie, proto se mu říká Pythagoras ze Samosu. V rodině kamenosochaře, který našel spíše slávu než bohatství. Už jako dítě projevoval mimořádné schopnosti, a když vyrostl, neklidná fantazie mladého muže se tísnila na malém ostrůvku.

Pythagoras Pythagoras se přestěhoval do města Mileyus a stal se žákem Thalese, kterému v té době táhlo na osmdesátku. Moudrý vědec poradil mladému muži, aby odešel do Egypta, kde sám kdysi studoval vědu. Před Pythagorem se otevřela neznámá země. Zarazilo ho, že v jeho rodném Řecku byli bohové v podobě lidí a egyptští bohové – v podobě napůl lidí – napůl zvířat. Znalosti byly soustředěny v chrámech, do kterých byl omezený přístup.

Pythagorovi trvalo roky, než hluboce prostudoval egyptskou kulturu, než mu bylo dovoleno seznámit se se staletými úspěchy egyptské vědy. Když Pythagoras pochopil vědu egyptských kněží, šel domů, aby tam založil vlastní školu. Kněží, kteří nechtěli šířit své znalosti mimo chrámy, ho nechtěli pustit. S velkými obtížemi se mu podařilo tuto překážku překonat.

Nicméně na cestě domů byl Pythagoras zajat a skončil v Babylonu. Babyloňané si vážili chytrých lidí, a tak si našel své místo mezi babylonskými mudrci. Babylonská věda byla rozvinutější než egyptská. Nejmarkantnější byly úspěchy algebry Pythagoras Babyloňané vynalezli a používali poziční číselnou soustavu při počítání, byli schopni řešit lineární, kvadratické a některé typy kubických rovnic. Pythagoras žil v Babylonu asi deset let a do vlasti se vrátil ve čtyřiceti letech. Na ostrově Samos ale dlouho nezůstal. Na protest proti tyranovi Polykratovi, který tehdy ostrovu vládl, se usadil v jedné z řeckých kolonií jižní Itálie ve městě Crotone.

Tam Pythagoras zorganizoval tajný svazek mládeže ze zástupců aristokracie. Toto spojení bylo po dlouhých zkouškách přijato s velkými ceremoniemi. Každý vstupující se zřekl svého majetku a složil přísahu, že zachová učení zakladatele v tajnosti. Pythagorejci, jak byli později nazýváni, se zabývali matematikou, filozofií a přírodními vědami. Škola měla vyhlášku, podle které bylo autorství všech matematických prací připisováno učiteli. Spojení Pythagorejců bylo tajné. Znakem či identifikačním znakem svazu byl pentagram – pěticípá hvězda. Pentagramu byla dána schopnost chránit člověka před zlými duchy.

Pythagorejci učinili mnoho důležitých objevů v aritmetice a geometrii. Je také známo, že vedle duchovního a mravního rozvoje Pythagorových žáků šlo o rozvoj fyzický. Nejenže se sám zúčastnil olympijských her a vyhrál dvě pěstní pěsti, ale také vychoval galaxii velkých olympioniků v době lidového povstání. Po jeho smrti studenti opředili jméno svého učitele mnoha legendami.

V babylonských textech se vyskytuje 1200 let před Pythagorem. Zřejmě byl první, kdo našel její důkaz. V tomto ohledu byl proveden následující záznam: "... když zjistil, že v pravoúhlém trojúhelníku přepona odpovídá nohám, obětoval býka z pšeničného těsta." Historie Pythagorovy věty Historie Pythagorovy věty je zajímavá. Přestože je tato věta spojena se jménem Pythagoras, byla známá již dávno před ním.



Věta V pravoúhlém trojúhelníku je druhá mocnina přepony rovna součtu čtverců nohou. Dáno: Δ ABC, C = 90° Dokaž: Důkaz: D Uvážíme-li cos B, dostaneme: Sečtením (1) a (2) dostaneme: Uvážíme-li cos B, dostaneme: Snižme výšku SD od vrcholu pravý úhel


snímek 2
a2+b2=c2 c a b P
snímek 3
Pythagoras tuto vlastnost pravoúhlého trojúhelníku neobjevil, byl pravděpodobně první, kdo ji zobecnil a dokázal, čímž ji přenesl z oblasti praxe do oblasti vědy. Nevíme, jak to udělal. Předpokládá se, že nicméně Pythagorův důkaz nebyl zásadní, ale pouze potvrzením, ověřením této vlastnosti na řadě konkrétních typů trojúhelníků, počínaje rovnoramenným pravoúhlým trojúhelníkem, pro který zjevně vyplývá z Obr. 1.
snímek 4
snímek 5
Důkazy založené na použití konceptu stejné oblasti čísel.
snímek 6
Je jasné, že pokud odečteme čtyřnásobnou plochu pravoúhlého trojúhelníku s nohami a, b od plochy čtverce, zůstanou stejné plochy, tj. c2 = a2 + b2. Staří hinduisté, jimž tato úvaha patří, ji však obvykle nezapsali, ale doprovázeli kresbu pouze jedním slovem: „Podívejte se!“ Je docela možné, že stejný důkaz nabídl i Pythagoras.
Snímek 7
aditivní důkaz. Tyto důkazy jsou založeny na rozkladu čtverců postavených na nohách do obrazců, z nichž je možné přidat čtverec postavený na přeponě. Einsteinův důkaz (obr. 3) je založen na rozkladu čtverce postaveného na přeponě na 8 trojúhelníků.
Snímek 8
Na Obr. 4 ukazuje důkaz Pythagorovy věty pomocí rozdělení al-Nairiziya, středověkého bagdádského komentátora Euklidových „Počátků“. V této přepážce je čtverec postavený na přeponě rozdělen na 3 trojúhelníky a 2 čtyřúhelníky. Zde: ABC je pravoúhlý trojúhelník s pravým úhlem C; DE = BF. Dokažte větu pomocí tohoto oddílu. D E
Snímek 9
Důkazy metodou rozšíření. Podstata této metody spočívá v tom, že ke čtvercům postaveným na nohách a ke čtverci postavenému na přeponě se připojují stejné figury tak, že se získají figury stejné velikosti.
Snímek 10
Platnost Pythagorovy věty vyplývá ze stejné velikosti šestiúhelníků AEDFPB a ACBNMQ. F
snímek 11
Na Obr. 13 ABC - obdélník, C - pravý úhel, CM AB, b1 - průmět nohy b na přeponu, a1 - průmět nohy a na přeponu, h - výška trojúhelníku nakresleného na přeponu. Protože ABC je podobné ACM, vyplývá z toho, že b2 = c*b1; (1) protože ABC je podobné BCM, vyplývá z toho, že a2 = c*a1. (2) Sečtením rovností (1) a (2) člen po členu dostaneme a2 + b2 = c*b1 + c*a1 = c*(b1 + a1) = c2. b
snímek 12
Na obrázku 15 tvoří tři pravoúhlé trojúhelníky lichoběžník. Proto lze plochu tohoto obrázku nalézt podle vzorce pro oblast obdélníkového lichoběžníku nebo jako součet ploch tří trojúhelníků. Garfieldův důkaz.
snímek 13
Životopis Pythagora. Velký vědec Pythagoras se narodil kolem roku 570 před naším letopočtem. na ostrově Samos. Pythagorův otec byl Mnesarchos, řezbář drahokamů. Jméno Pythagorovy matky není známo. Podle mnoha starověkých svědectví byl narozený chlapec pohádkově hezký a brzy ukázal své vynikající schopnosti. Mezi učiteli mladého Pythagora patřili starší Germodamant a Pherekides ze Syrosu. Mladý Pythagoras trávil celé dny u nohou staršího Herma a poslouchal melodie cithary a Homérových hexametrů. Vášeň pro hudbu a poezii velkého Homéra si Pythagoras zachoval po celý život. A jako uznávaný mudrc, obklopený davem studentů, začal Pythagoras den zpěvem jedné z Homérových písní. Pherecydes byl filozof a byl považován za zakladatele italské filozofické školy. Ale ať je to jak chce, neklidná fantazie mladého Pythagora se brzy naplnila na malém Samosovi a on se vydává do Milétu, kde se setkává s dalším vědcem Thalesem. Thales mu radí, aby se vydal za poznáním do Egypta, což Pythagoras udělal. V roce 548 př.n.l Pythagoras dorazil do Navcratis, kolonie Samian, kde byl někdo, kdo našel úkryt a jídlo.
Snímek 14
Po studiu jazyka a náboženství Egypťanů odjíždí do Memphisu. Navzdory faraónovu doporučujícímu dopisu mazaní kněží nijak nespěchali, aby odhalili svá tajemství Pythagorovi a nabídli mu těžké zkoušky. Ale Pythagoras, hnán touhou po vědění, všechny přemohl, i když podle vykopávek ho egyptští kněží nemohli mnoho naučit, protože. v té době byla egyptská geometrie čistě aplikovanou vědou (uspokojující tehdejší potřebu počítání a měření země). Proto, když se dozvěděl vše, co mu kněží dali, utekl od nich a přestěhoval se do své vlasti v Hellas. Když však Pythagoras urazil část cesty, rozhodne se pro cestu po zemi, během níž byl zajat Kambýsem, babylonským králem, který mířil domů. Život Pythagora v Babylonu není nutné dramatizovat, protože velký vládce Kýros byl tolerantní ke všem zajatcům. Babylonská matematika byla nepopiratelně pokročilejší (příkladem toho je poziční systém počtu) než egyptská a Pythagoras se musel hodně učit. Ale v roce 530 př.n.l. Cyrus se vydal na tažení proti kmenům ve Střední Asii. A Pythagoras využil rozruchu ve městě a uprchl do své vlasti.
Snímek 15
A na Samosu v té době vládl tyran Polykrates. Pythagoras samozřejmě nebyl spokojen se životem dvorního polootroka a odešel do jeskyní v okolí Samosu. Po několika měsících nároků od Polykrata se Pythagoras stěhuje do Crotonu. V Krotónu Pythagoras založil něco jako nábožensko-etické bratrstvo nebo tajný mnišský řád („Pythagorejci“), jehož členové byli povinni vést tzv. pythagorejský způsob života. Byla to zároveň náboženská unie, politický klub a vědecká společnost. Je třeba říci, že některé zásady hlásané Pythagorem jsou hodné napodobování i nyní. ...je to 20 let. Sláva bratrství se rozšířila po celém světě. Jednoho dne Cylon, bohatý, ale zlý muž, přichází k Pythagorovi, který se chce v opilosti připojit k bratrstvu. Poté, co byl Cylon odmítnut, zahájí boj s Pythagorasem a využije žhářství jeho domu. Pythagorejci při požáru zachránili na vlastní náklady život svému učiteli, načež se Pythagorasovi stýskalo po domově a brzy spáchal sebevraždu.
Zobrazit všechny snímky
Historie věty. Starověká Čína Začněme náš historický přehled starověkou Čínou. Zde přitahuje zvláštní pozornost matematická kniha Chu-peie. Tato esej říká o Pythagorejském trojúhelníku se stranami 3, 4 a 5 toto: Začněme historický přehled starověkou Čínou. Zde přitahuje zvláštní pozornost matematická kniha Chu-peie. Tato esej říká o pythagorejském trojúhelníku se stranami 3, 4 a 5 toto: „Pokud se pravý úhel rozloží na jednotlivé části, pak čára spojující konce jeho stran bude 5, když základna je 3 a výška je 4. ." Ve stejné knize je navržena kresba, která se shoduje s jednou z kreseb hinduistické geometrie Bashara. Ve stejné knize je navržena kresba, která se shoduje s jednou z kreseb hinduistické geometrie Bashara.
Poněkud více je známo o Pythagorově větě mezi Babyloňany. V jednom textu pocházejícím z doby Hammurabiho, tedy do roku 2000 před naším letopočtem. e. je uveden přibližný výpočet přepony pravoúhlého trojúhelníku. Z toho můžeme usoudit, že v Mezopotámii byli schopni provádět výpočty s pravoúhlými trojúhelníky, alespoň v některých případech. Geometrie u Hindů, stejně jako u Egypťanů a Babyloňanů, byla úzce spjata s kultem. Je velmi pravděpodobné, že věta o čtverci přepony byla známa již v Indii kolem 18. století před naším letopočtem. E. starověká Indie

Kantor (největší německý historik matematiky) věří, že rovnost: 3² + 4² = 5² byla Egypťanům známa již kolem roku 2300 př.nl. př. n. l., za dob krále Amenemhata I. (podle Papyru 6619 Berlínského muzea) Podle Cantora harpedonapty neboli „napínače strun“ stavěly pravé úhly pomocí pravoúhlých trojúhelníků se stranami 3, 4 a 5. Je to velmi snadno reprodukovat jejich způsob konstrukce. Vezměte lano dlouhé 12 metrů a přivažte ho k němu po barevném pruhu ve vzdálenosti 3 metry od jednoho konce a 4 metry od druhého. Mezi stranami o délce 3 a 4 metry bude uzavřen pravý úhel.

Na jedné straně na základě současné úrovně znalostí o egyptské a babylonské matematice a na druhé straně na základě kritického studia řeckých pramenů dospěl Van der Waerden (nizozemský matematik) k závěru: „Zásluhy prvních řeckých matematiků , jako byli Thales, Pythagoras a Pythagorejci, není objevem matematiky, ale její systematizací a zdůvodněním. V jejich rukou se výpočetní recepty založené na vágních představách proměnily v exaktní vědu."


Velký vědec Pythagoras se narodil kolem roku 570 před naším letopočtem. na ostrově Samos. Pythagorův otec byl Mnesarchos, řezbář drahokamů. Jméno Pythagorovy matky není známo. Podle mnoha starověkých svědectví byl narozený chlapec pohádkově hezký a brzy ukázal své vynikající schopnosti. Vášeň pro hudbu a poezii velkého Homéra si Pythagoras zachoval po celý život. Neklidná představivost mladého Pythagora se brzy naplnila na malém Samosovi a on odchází do Milétu, kde se setkává s dalším vědcem Thalesem. Poté se vydá na cestu a je zajat babylonským králem Kýrem. V roce 530 př.n.l Cyrus se vydal na tažení proti kmenům ve Střední Asii. A Pythagoras využil rozruchu ve městě a uprchl do své vlasti.

A na Samosu v té době vládl tyran Polykrates. Po několika měsících nároků od Polykrata se Pythagoras stěhuje do Crotonu. V Krotónu založil Pythagoras něco jako nábožensko-etické bratrstvo nebo tajný mnišský řád („Pythagorejci“), jehož členové byli povinni vést tzv. pythagorejský způsob života....Uplynulo dvacet let. Sláva bratrství se rozšířila po celém světě. Jednoho dne Cylon, bohatý, ale zlý muž, přichází k Pythagorovi, který se chce v opilosti připojit k bratrstvu. Poté, co byl Cylon odmítnut, zahájí boj s Pythagorasem a využije žhářství jeho domu. Pythagorejci při požáru zachránili na vlastní náklady život svému učiteli, načež se Pythagorasovi stýskalo po domově a brzy spáchal sebevraždu.


Pythagorova věta. V pravoúhlém trojúhelníku se čtverec přepony rovná součtu čtverců nohou. Další formulace věty. V Euklidovi tato věta zní (doslovný překlad): "V pravoúhlém trojúhelníku se čtverec strany natažené přes pravý úhel rovná čtvercům na stranách, které svírají pravý úhel." V Geometria Culmonensis (cca 1400) v překladu zní věta takto: „Takže plocha čtverce, měřená podél dlouhé strany, je stejně velká jako plocha dvou čtverců, které se měří na dvou jeho stranách. vedle pravého úhlu."

Nejjednodušší důkaz. Nejjednodušší důkaz věty získáme v nejjednodušším případě rovnoramenného pravoúhlého trojúhelníku. Vskutku, stačí se jen podívat na skládání rovnoramenných pravoúhlých trojúhelníků, abychom viděli, že věta je pravdivá. Například pro trojúhelník ABC: čtverec postavený na přeponě AC obsahuje 4 počáteční trojúhelníky a čtverce postavené na nohách obsahují dva.

Důkaz odčítáním. Seznámíme se s dalším důkazem metodou odčítání. Známou kresbu Pythagorovy věty uzavřeme do obdélníkového rámečku, jehož směry stran se shodují se směry nohou trojúhelníku. Pokračujme v některých segmentech obrázku, jak je znázorněno na obrázku, zatímco obdélník se rozpadne na několik trojúhelníků, obdélníků a čtverců. Nejprve odeberme z obdélníku několik částí tak, aby zůstal pouze čtverec postavený na přeponě. Tyto části jsou následující: 1. trojúhelníky 1, 2, 3, 4; 2. obdélník 5; 3. obdélník 6 a čtverec 8; 4. obdélník 7 a čtverec 9;

Poté díly z obdélníku vyhodíme tak, aby zůstaly jen čtverce postavené na nožičkách. Tyto části budou: 1. obdélníky 6 a 7; 2. obdélník 5; 3. obdélník 1 (stínovaný); 4. obdélník 2 (stínovaný); Zbývá nám pouze ukázat, že odečtené části jsou stejné. To je dobře vidět díky uspořádání figurek. Z obrázku je zřejmé, že: 1. obdélník 5 má stejnou velikost; 2. čtyři trojúhelníky 1,2,3,4 se svou plochou rovnají dvěma obdélníkům 6 a 7; 3. obdélník 6 a čtverec 8 dohromady mají stejnou velikost jako obdélník 1 (stínovaný); 4. obdélník 7 spolu se čtvercem 9 mají stejnou plochu jako obdélník 2 (stínovaný); Věta prokázaná

Einsteinův důkaz Body E, C a F leží na stejné přímce; to vyplývá z jednoduchých výpočtů mírové míry úhlu ECF (je rozvinutý). CD je nakresleno kolmo k EF. Levá a pravá strana čtverce postaveného na přeponě pokračuje vzhůru ke křižovatce s EF; boční EA je prodloužena až k průsečíku s CD. Stejné trojúhelníky jsou tedy stejně očíslovány.

Ve skutečnosti jsou trojúhelníky ABD a BFC stejné ve dvou stranách a úhlu mezi nimi: FB = AB, BC = BD a úhly mezi nimi jsou stejné jako tupé úhly se vzájemně kolmými stranami. S ABD \u003d 0,5 S BJLD, protože trojúhelník ABD a obdélník BJLD mají společnou základnu BD a společnou výšku LD. Podobně S FBC=0,5 S ABFH (BF-společná základna, AB-společná výška). Pokud tedy vezmeme v úvahu, že S ABD= S FBC, máme S BJLD= S ABFH. Podobně, pokud nakreslíte segment AE pomocí rovnosti trojúhelníků BCK a ACE, dokážete, že S JCEL = S ACKG. Takže S ABFH+ S ACKG= S BJLD+ S JCEL= S BCED, což mělo být prokázáno. Tento důkaz podal Euklides ve svých Živlech. Podle Prokla (Byzanc) jej vynalezl sám Eukleidés. Euklidův důkaz je uveden ve výroku 47 první knihy Počátků. Na přeponu a ramena pravoúhlého trojúhelníku ABC se sestrojí příslušné čtverce a je dokázáno, že obdélník BJLD se rovná čtverci ABFH a obdélník JCEL se rovná čtverci AGKS. Potom se součet ploch čtverců na nohách bude rovnat ploše čtverce na přeponě.



Druhou záhadou je blíže nespecifikovaný počet důkazů slavné Pythagorovy věty o Samose. Právě při této příležitosti jsem se rozhodl provést sociologický průzkum, který ukázal, že většina starší generace souhlasí s existencí 250 důkazů, i když z dalších zdrojů vím, že existuje více než 350 důkazů této věty, takže dokonce dostali do Guinessovy knihy rekordů! Ale samozřejmě je v těchto důkazech použito relativně málo zásadně odlišných myšlenek.

Třetí záhadou je, že Pythagorova věta je dnes symbolem matematiky. Čtvrté tajemství – Pythagorova věta nám poskytuje nejbohatší materiál pro zobecnění – nejdůležitější druh duševní činnosti, základ teoretického myšlení, kterým se mnozí vědci vyznají. Zde můžeme dodat, že od Pythagorovy věty lze přejít k větám jiným.

Pátou záhadou je, že někteří učenci připisují Pythagorovi důkaz, který Euklides podal v první knize svých Živlů. Na druhé straně Proclus (matematik 5. století) tvrdil, že důkaz v Elementech byl způsoben samotným Euklidem. Ale přesto dnes zůstává metoda dokazování Pythagoras neznámá.

Šestou záhadou jsou legendy o samotném Pythagorovi, muži, který jako první dokázal tuto větu. Existuje legenda, že když Pythagoras ze Samosu dokázal svou větu, poděkoval bohům obětováním 100 býků. Existovaly také legendy o hypnotických schopnostech vědce: jako by jediným pohledem mohl změnit směr letu ptáků. A také řekli, že tato úžasná osoba byla současně viděna v různých městech, mezi nimiž bylo několik dní cestování. A že prý vlastnil „kolo štěstí“, jehož otáčením nejen předpovídal budoucnost, ale v případě potřeby i zasahoval do běhu událostí.

Popis prezentace na jednotlivých snímcích:
1 snímek
Popis snímku:
Lyceum teacher ve společnosti KazGASA Auelbekova G.U. "Pythagorova věta a různé způsoby, jak ji dokázat." 2016
2 snímek
Popis snímku:
CÍL: Hlavním úkolem je zvážit různé způsoby důkazu Pythagorovy věty. Ukázat význam Pythagorovy věty pro rozvoj vědy a techniky, v matematice obecně.
3 snímek
Popis snímku:
Z životopisu Pythagora To nejvíce, co je nyní obyvatelstvu známo o tomto respektovaném starověkém Řekovi, zapadá do jedné věty: "Pythagorejské kalhoty jsou stejné na všech stranách." Autory tohoto teaseru od Pythagora jasně dělí staletí, jinak by se neodvážili škádlit. Protože Pythagoras není vůbec druhou mocninou přepony, rovna součtu čtverců nohou. Toto je slavný filozof. Pythagoras žil v šestém století před naším letopočtem, měl krásný vzhled, nosil dlouhé vousy a na hlavě zlatý diadém. Pythagoras není jméno, ale přezdívka, kterou filozof dostal za to, že vždy mluvil správně a přesvědčivě, jako řecký orákulum. (Pythagoras - "přesvědčovací řeč".) Svými projevy získal 2000 studentů, kteří spolu se svými rodinami vytvořili školní stát, kde platily Pythagorovy zákony a pravidla. Byl první, kdo pojmenoval svou práci. Slovo „filosof“ k nám stejně jako slovo „kosmos“ přišlo od Pythagora. V jeho filozofii je hodně prostoru. Tvrdil, že k pochopení Boha, člověka a přírody je třeba studovat algebru s geometrií, hudbou a astronomií. Mimochodem, právě pythagorejský systém vědění se v řečtině nazývá „matematika“. Pokud jde o notoricky známý trojúhelník s přeponou a nohami, je to podle velkého Řeka více než jen geometrická postava. To je „klíč“ ke všem zašifrovaným jevům našeho života. Všechno v přírodě, řekl Pythagoras, je rozděleno do tří částí. Proto před řešením jakéhokoli problému musí být prezentován ve formě trojúhelníkového diagramu. "Podívejte se na trojúhelník - a problém je ze dvou třetin vyřešen."
4 snímek
Popis snímku:
Nyní existují tři formulace Pythagorovy věty: 1. V pravoúhlém trojúhelníku je druhá mocnina přepony rovna součtu čtverců nohou. 2. Plocha čtverce postaveného na přeponě pravoúhlého trojúhelníku se rovná součtu ploch čtverců postavených na nohách. 3. Čtverec postavený na přeponě pravoúhlého trojúhelníku je stejně vzdálený se čtverci postavenými na nohách. Inverzní Pythagorova věta: Pro libovolnou trojici kladných čísel a, b a c taková, že a2 + b2 = c2, existuje pravoúhlý trojúhelník s rameny a a b a přeponou c. vy
5 snímek
Popis snímku:
Z historie teorému Z historie teorému Přísně vzato, ačkoli se teorém nazývá „Pythagorova věta“, Pythagoras sám ji neobjevil. Pravoúhlý trojúhelník a jeho speciální vlastnosti byly studovány dávno před ním. Na tuto otázku existují dva polární pohledy. Podle jedné verze byl Pythagoras první, kdo našel úplný důkaz teorému. Podle jiného důkaz nepatří k autorství Pythagora. Dnes již nelze kontrolovat, kdo má pravdu a kdo ne. Ví se pouze, že důkaz o Pythagorovi, pokud vůbec existoval, se nedochoval. Existují však návrhy, že slavný důkaz z Euklidových prvků může patřit Pythagorovi a Euklides jej pouze zaznamenal. Dnes je také známo, že problémy o pravoúhlém trojúhelníku se nacházejí v egyptských pramenech z doby faraona Amenemheta I., na babylonských hliněných tabulkách z doby vlády krále Hammurabiho, ve starověkém indickém pojednání Sulva Sutra a starověkém čínském díle Zhou -bi suan jin. Jak vidíte, Pythagorova věta zaměstnávala mysl matematiků již od starověku. Jako potvrzení slouží přibližně 500 různých důkazů, které dnes existují. Žádná jiná věta jí v tomto ohledu nemůže konkurovat. Mezi významné autory důkazů patří Leonardo da Vinci a 20. prezident Spojených států James Garfield. To vše vypovídá o mimořádné důležitosti této věty pro matematiku: většina vět o geometrii je z ní odvozena nebo s ní tak či onak spojena. .
6 snímek
Popis snímku:
Výroky Výroky věty přeložené z řečtiny, latiny a němčiny V Euklidovi tato věta zní (doslovný překlad): „V pravoúhlém trojúhelníku se čtverec strany natažené přes pravý úhel rovná čtvercům na stranách, které uzavírají pravý úhel." Latinský překlad arabského textu Annairici (asi 900 př. n. l.), který vytvořil Gerhard z Clemons (začátek 12. století), přeložený do ruštiny zní: „V každém pravoúhlém trojúhelníku se čtverec vytvořený na straně táhl přes pravý úhel se rovná součtu dvou čtverců vytvořených na dvou stranách, které svírají pravý úhel. V Geometria Culmonensis (cca 1400) v překladu zní věta takto: „Takže plocha čtverce, měřená podél dlouhé strany, je stejně velká jako plocha dvou čtverců, které se měří na dvou jeho stranách. vedle pravého úhlu." V prvním ruském překladu euklidovských „Počátků“, který provedl F. I. Petruševskij, je Pythagorova věta uvedena takto: „V pravoúhlých trojúhelníkech se čtverec strany protilehlé pravému úhlu rovná součtu čtverců strany obsahující pravý úhel."
7 snímek
Popis snímku:
Konstrukce použitá pro důkaz je následující: pro pravoúhlý trojúhelník s pravým úhlem, čtverce přes nohy a a čtverec nad přeponou se sestrojí výška a paprsek, který v ní pokračuje a rozděluje čtverec přes přeponu. na dva obdélníky a. Důkaz je zaměřen na stanovení rovnosti ploch obdélníku se čtvercem nad ramenem, rovnosti ploch druhého obdélníku, který je druhou mocninou přepony, a obdélníku nad druhým ramenem podobným způsobem. . Rovnost ploch obdélníku a je stanovena kongruencí trojúhelníků a plocha každého z nich se rovná polovině plochy čtverců, respektive ve spojení s následující vlastností: plocha trojúhelníku se rovná polovině plochy obdélníku, pokud mají postavy společnou stranu, a výška trojúhelníku ke společné straně je druhá strana obdélníku. Shoda trojúhelníků vyplývá z rovnosti dvou stran (strany čtverců) a úhlu mezi nimi (složeného z pravého úhlu a úhlu u. Důkaz tedy stanoví, že plocha čtverce nad přeponou , složený z obdélníků a, je roven součtu ploch čtverců nad nohama. JEDNODUCHÝ DŮKAZ
8 snímek
Popis snímku:
AJ je výška odečtená od přepony. Dokažme, že jeho pokračování rozděluje čtverec postavený na přeponě na dva obdélníky, jejichž plochy se rovnají plochám odpovídajících čtverců postavených na nohách. Dokažme, že obdélník BJLD je svou plochou roven čtverci ABFH. Trojúhelník ABD=BFC (na dvou stranách a úhel mezi nimi BF=AB; BC=BD; úhel FBC=úhel ABD).
9 snímek
Popis snímku:
S trojúhelníku ABD=1/2 S obdélníku BJLD, protože Triangle ABD a Rectangle BJLD mají společnou základnu BD a společnou výšku LD. PODOBNĚ S trojúhelníku FBC=1/2 S obdélníku ABFH(BF-společná základna, AB-společná výška). Uvážíme-li tedy, že S trojúhelníku ABD =S trojúhelníku FBC, máme: S BJLD=S ABFH. PODOBNĚ pomocí rovnosti trojúhelníků BCK a ACE je dokázáno, že S JCEL=S ACKG. S ABFH+S ACKJ=S BJLD+ S JCEL=S BCED. Trojúhelník S=1/2AB x BD=1/2LD x BD=1/2 S BJLD Věta je dokázána. A L B D
10 snímek
Popis snímku:
Důkaz indického matematika Bhaskariho (a - c) ². To znamená, že se ukazuje, že c ² \u003d 4 0,5 a b + (a - c) ² c ² \u003d 2 a b + a ² - 2 a b + c ² c ² \u003d a ² + c ² Věta je prokázána.
11 snímek
Popis snímku:
Waldheimův důkaz а в са в с Waldheim využívá skutečnosti, že plocha pravoúhlého trojúhelníku je rovna polovině součinu jeho ramen a plocha lichoběžníku je rovna součinu poloviny součtu rovnoběžky. základny a výšku. Nyní, abychom dokázali větu, stačí vyjádřit obsah lichoběžníku dvěma způsoby S lichoběžník = 0,5 (a + b) (a + b) = 0,5 (a + b) ² S lichoběžník = 0,5 a b + 0, 5 a b + 0,5 s ² Porovnáním správných částí dostaneme 0,5 (a + b) ² \u003d 0,5 a b + 0,5 a b + 0,5 s ² (a + b) ² \u003d a b + a c + c ² a ² + 2 a c + c ² = 2 a c + c ² c ² = a ² + c ² Věta je dokázána
12 snímek
Popis snímku:
Hawkinsův důkaz A B C A1 B1 a c D c a c c 1. Otočte obdélníkový ∆ABC (s pravým úhlem C) kolem středu v bodě C o 90º tak, aby zaujal pozici A1 B1 C, jak je znázorněno na obrázku. 2. Pokračujeme v přeponě B1 A1 za bod A1, dokud se neprotne s přímkou AB v bodě D. Úsek B1 D bude ∆B1AB (protože ∟B1DA = 90º). 3. Uvažujme čtyřúhelník A1AB1B. Na jedné straně SA1AB1B \u003d SCAA1 + SSBB1 \u003d 0,5v + 0,5a a \u003d 0,5 (a² + b²) PEKLO \u003d \u003d 0,5 s (HELL + VD) \u003d rovná se 0,5 s 0,5 (a² + b²) \u003d 0,5 s² a² + b² \u003d s² Věta je dokázána.
13 snímek
Popis snímku:
geometrický důkaz. (Hoffmannova metoda) Sestrojme trojúhelník ABC s pravým úhlem C. Sestrojme BF=CB, BFCB Sestrojme BE=AB, BEAB Sestrojme AD=AC, ADAC Body F, C, D patří jedné přímce .
14 snímek
Popis snímku:
Jak vidíme, čtyřúhelníky ADFB a ACBE jsou stejně velké, protože ABF=ECB. Trojúhelníky ADF a ACE jsou stejné. Odečtěte od obou stejně velkých čtyřúhelníků pro ně společný trojúhelník ABC, dostaneme: 1/2а2+1/2b 2=1/2с 2 Odpovídajícím způsobem: a2+ b 2 =с 2 Věta je dokázána.
15 snímek
Popis snímku:
Algebraický důkaz (Mölmannova metoda) Plocha tohoto obdélníku se rovná 0,5ab na jedné straně a 0,5pr na druhé straně, kde p je semiperimetr trojúhelníku, r je poloměr kružnice do něj vepsané (r = 0,5 (a+b-c)). A C
16 snímek
Popis snímku:
Máme: 0,5ab=0,5pr=0,5(a+b+c)*0,5(a+b-c) Z toho plyne, že c2= a2+b2 Věta je dokázána. A C
17 snímek
Popis snímku:
Význam Pythagorovy věty Pythagorova věta je právem jednou ze základních teorémů matematiky. Význam této věty spočívá v tom, že s její pomocí je možné odvodit většinu vět v geometrii. Jeho hodnota v moderním světě je také velká, protože Pythagorova věta se používá v mnoha oblastech lidské činnosti. Používá se například při umisťování hromosvodů na střechách budov, při výrobě oken některých architektonických stylů a dokonce i při výpočtech výšky antén mobilních operátorů. A to není celý seznam praktických aplikací této věty. Proto je velmi důležité znát Pythagorovu větu a rozumět jejímu významu.
18 snímek
Popis snímku:
Pythagorova věta v literatuře. Pythagoras je nejen skvělý matematik, ale také velký myslitel své doby.Seznámíme se s některými jeho filozofickými výroky ...
19 snímek
Popis snímku:
1. Myšlení je především mezi lidmi na zemi. 2. Nesedejte si na obilnou míru (t. j. nežijte nečinně). 3. Při odchodu se neohlížej (tedy před smrtí neulpívej na životě). 4. Nechoďte po vyšlapaných cestách (to znamená, že se neřiďte názory davu, ale názory těch pár, kteří rozumí). 5. Nenechávejte v domě vlaštovky (t. j. nepřijímejte hosty, kteří jsou upovídaní a nejsou zdrženliví v jazyce). 6. Buď s tím, kdo břemeno bere, nebuď s tím, kdo břemeno odhazuje (to je povzbuzuj lidi ne k zahálce, ale ke ctnosti, k práci). 7. Nenoste obrazy v prstenu (t. j. nechoďte před lidmi, jak soudíte a přemýšlíte o bozích).
Černov Maxim
Projekt o geometrii, koncipovaný jako prezentace na téma "Pythagorova věta a různé způsoby jejího dokazování"
Stažení:
Náhled:
Chcete-li používat náhled prezentací, vytvořte si účet Google (účet) a přihlaste se: https://accounts.google.com
Popisky snímků:
Pythagorova věta a různé způsoby jejího dokazování Vyplnil: Černov Maxim 8A
Účel projektu: Vyslovit Pythagorovu větu, představit různé způsoby jejího dokazování.
Historie Starověká čínská kniha Zhou bi suan jing mluví o pythagorejském trojúhelníku se stranami 3, 4 a 5. Ve stejné knize je navržena kresba, která se shoduje s jednou z kreseb hinduistické geometrie Baskhary. Moritz Cantor (největší německý historik matematiky) se domnívá, že rovnost 3 ² + 4 ² = 5 ² znali Egypťané již kolem roku 2300 př. n. l., v době krále Amenemheta I. (podle papyru 6619 Berlínského muzea). Podle Cantora harpedonapty neboli „napínače strun“ stavěly pravé úhly pomocí pravoúhlých trojúhelníků se stranami 3, 4 a 5. Je velmi snadné reprodukovat jejich konstrukční metodu. Vezmeme lano dlouhé 12 m a přivážeme ho k němu po barevném pruhu ve vzdálenosti 3 m od jednoho konce a 4 metry od druhého. Mezi stranami o délce 3 a 4 metry bude uzavřen pravý úhel. Harpedonaptům by se dalo namítnout, že jejich způsob stavby se stane nadbytečným, pokud se například použije dřevěný čtverec, který používají všichni tesaři. Jsou totiž známy egyptské kresby, ve kterých se takový nástroj nachází – například kresby zobrazující truhlářskou dílnu. Poněkud více je známo o Pythagorově větě mezi Babyloňany. V jednom textu z doby Hammurabiho, tedy do roku 2000 př. n. l., je uveden přibližný výpočet přepony rovnoramenného pravoúhlého trojúhelníku. Z toho můžeme usoudit, že v Mezopotámii byli schopni provádět výpočty s pravoúhlými trojúhelníky, alespoň v některých případech. Na jedné straně na základě současné úrovně znalostí egyptské a babylonské matematiky a na druhé straně na základě kritického studia řeckých pramenů dospěl van der Waerden (nizozemský matematik) k závěru, že existuje vysoká pravděpodobnost, že věta o čtverci přepony byla známa v Babylonu kolem 18. století před naším letopočtem. E. Podle Proklova komentáře k Euklidovi použil Pythagoras (o kterém se obecně předpokládá, že žil mezi lety 570-490 př. n. l.) algebraické metody k nalezení pythagorejských trojic. Nicméně, Proclus psal mezi 410 a 485. n. E. Thomas Little Heath věřil, že neexistuje žádná výslovná zmínka, pocházející z období 5 století po Pythagorově smrti, že Pythagoras byl autorem věty. Když však autoři jako Plutarchos a Cicero píší o Pythagorově větě, píší, jako by autorství Pythagora bylo všeobecně známé a jisté.období Pythagorovy matematiky. Podle legendy oslavil Pythagoras objevení své věty obří hostinou, kdy na oslavu porazil sto býků. Kolem roku 400 př.n.l. e., podle Proclus, Plato dal metodu pro nalezení Pythagorean trojice, kombinovat algebru a geometrii. Kolem roku 300 př. Kr. E. v Euklidově Principia se objevil nejstarší axiomatický důkaz Pythagorovy věty.
Výroky: Geometrická formulace: Původně byla věta formulována takto: V pravoúhlém trojúhelníku se plocha čtverce postaveného na přeponě rovná součtu ploch čtverců postavených na nohách. Algebraická formulace: V pravoúhlém trojúhelníku je druhá mocnina délky přepony rovna součtu druhých mocnin délek nohou. Tedy označení délky přepony trojúhelníku skrz, a délek ramen skrz a a b: a2+b2=c2 Obě formulace věty jsou ekvivalentní, ale druhá formulace je elementárnější, nevyžaduje koncept oblasti. To znamená, že druhé tvrzení lze ověřit, aniž bychom věděli cokoli o ploše a měřením pouze délek stran pravoúhlého trojúhelníku.
Důkazy V současné době je ve vědecké literatuře zaznamenáno 367 důkazů této věty. Pravděpodobně je Pythagorova věta jedinou větou s tak působivým počtem důkazů. Takovou rozmanitost lze vysvětlit pouze základním významem věty pro geometrii. Samozřejmě, koncepčně je lze všechny rozdělit do malého počtu tříd. Nejznámější z nich: důkazy plošnou metodou, axiomatické a exotické důkazy (např. pomocí diferenciálních rovnic).
Prostřednictvím podobných trojúhelníků Následující důkaz algebraické formulace je nejjednodušší z důkazů vytvořených přímo z axiomů. Zejména nepoužívá koncept plochy obrázku. Nechť ABC je pravoúhlý trojúhelník s pravým úhlem C . Nakreslete výšku z C a označte její základnu H . Trojúhelník ACH je podobný trojúhelníku ABC ve dvou úhlech. Podobně trojúhelník CBH je podobný ABC. Zavedením zápisu získáme Což je ekvivalentní Sečtením získáme nebo, které bylo potřeba dokázat
Důkazy plošnou metodou Následující důkazy i přes zdánlivou jednoduchost nejsou vůbec tak jednoduché. Všechny využívají plošných vlastností, jejichž důkaz je složitější než samotný důkaz Pythagorovy věty Důkaz ekvikomplementací Položme čtyři stejné pravoúhlé trojúhelníky, jak je znázorněno na obrázku 1. Čtyřúhelník o stranách c je čtverec, protože součet dvou ostrých úhlů je 90° a rozvinutý úhel je 180°. Plocha celého obrazce se na jedné straně rovná ploše čtverce se stranou (a + b) a na druhé straně součtu ploch čtyř trojúhelníků a plochy vnitřního náměstí. Q.E.D. .
Euklidův důkaz Myšlenka Euklidova důkazu je následující: zkusme dokázat, že polovina plochy čtverce postaveného na přeponě se rovná součtu polovičních ploch čtverců postavených na nohách, a pak plochy velkého a dvou malých čtverců jsou stejné. Zvažte výkres vlevo. Na něj jsme postavili čtverce po stranách pravoúhlého trojúhelníku a nakreslili paprsek s z vrcholu pravého úhlu C kolmo na přeponu AB, ten rozřízne čtverec ABIK, postavený na přeponě, na dva obdélníky - BHJI a HAKJ. , resp. Ukazuje se, že plochy těchto obdélníků jsou přesně stejné jako plochy čtverců postavených na odpovídajících nohách. Pokusme se dokázat, že plocha čtverce DECA se rovná ploše obdélníku AHJK. K tomu použijeme pomocné pozorování: Plocha trojúhelníku se stejnou výškou a základnou jako daný obdélník se rovná polovině plochy daného obdélníku. Je to důsledek definování plochy trojúhelníku jako poloviny součinu základny a výšky. Z tohoto pozorování vyplývá, že plocha trojúhelníku ACK se rovná ploše trojúhelníku AHK (nezobrazeno), což se zase rovná polovině plochy obdélníku AHJK. Nyní dokažme, že plocha trojúhelníku ACK se také rovná polovině plochy čtverce DECA. Jediné, co je pro to třeba udělat, je dokázat rovnost trojúhelníků ACK a BDA (protože plocha trojúhelníku BDA se rovná polovině plochy čtverce podle výše uvedené vlastnosti). Tato rovnost je zřejmá: trojúhelníky jsou stejné ve dvou stranách a úhlu mezi nimi. Totiž - AB=AK, AD=AC - rovnost úhlů CAK a BAD lze snadno dokázat pohybovou metodou: otočme trojúhelník CAK o 90° proti směru hodinových ručiček, pak je zřejmé, že odpovídající strany dvou uvažovaných trojúhelníků se budou shodovat. (vzhledem k tomu, že úhel ve vrcholu čtverce je 90°). Argument o rovnosti ploch čtverce BCFG a obdélníku BHJI je zcela analogický. Tím jsme dokázali, že plocha čtverce postaveného na přeponě je součtem ploch čtverců postavených na nohách. Myšlenka tohoto důkazu je dále ilustrována animací výše. Tento důkaz se také nazývá „pythagorejské kalhoty“.
Důkaz Leonarda da Vinci Hlavními prvky důkazu jsou symetrie a pohyb. Zvažte výkres, jak je vidět ze symetrie, segment rozřízne čtverec na dvě identické části (protože trojúhelníky a jsou stejné v konstrukci). Pomocí otočení o 90 stupňů proti směru hodinových ručiček kolem bodu vidíme rovnost stínovaných čísel a. Nyní je jasné, že plocha obrázku, kterou jsme vystínovali, se rovná součtu poloviny ploch malých čtverců (postavených na nohách) a plochy původního trojúhelníku. Na druhé straně se rovná polovině plochy velkého čtverce (postaveného na přeponě) plus plocha původního trojúhelníku. Poloviční součet ploch malých čtverců se tedy rovná polovině plochy velkého čtverce, a proto se součet ploch čtverců postavených na nohách rovná ploše postaveného čtverce. na přeponu.
Význam Pythagorovy věty Pythagorova věta je jednou z hlavních a dalo by se říci nejdůležitější věty geometrie. Jeho význam spočívá v tom, že z něj nebo s jeho pomocí lze odvodit většinu geometrických vět.
Děkuji za pozornost!