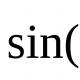Колебания и волны. Гармонические колебания Формулы нахождения амплитуды колебаний

4.2. Понятия и определения раздела «колебания и волны»

Уравнение гармонических колебаний и его решение:

, x=Acos(ω 0 t+ α) ,

A – амплитуда колебаний;

α – начальная фаза колебаний.

Период колебаний материальной точки, совершающей колебаний под действием силы упругости:

где m – масса материальной точки;

k – коэффициент жесткости.

Период колебаний математического маятника:

где l – длина маятника;

g = 9,8 м/с 2 – ускорение свободного падения.

Амплитуда колебаний, получаемых при сложении двух одинаково направленных гармонических колебаний:

где A 1 и А 2 – амплитуды слагаемых колебаний;

φ 1 и φ 2 – начальные фазы слагаемых колебаний.

Начальная фаза колебаний, получаемых при сложении двух одинаково направленных гармонических колебаний:

.

Уравнение затухающих колебаний и его решение:

, ,

– частота затухающих колебаний,

здесь ω 0 – собственная частота колебаний.

Логарифмический декремент затухания:

где β – коэффициент затухания;

– период затухающих колебаний.

Добротность колебательной системы:

где θ – логарифмический декремент затухания

Уравнение вынужденных колебаний и его установившееся решение:

, x=A cos(ωt- φ),

где F 0 – амплитудное значение силы;

– амплитуда затухающих колебаний;

φ= – начальная фаза.

Резонансная частота колебаний:

,

где ω 0 – собственная циклическая частота колебаний;

β – коэффициент затухания.

Затухающие электромагнитные колебания в контуре, состоящем из емкости C , индуктивности L и сопротивления R :

,

где q – заряд на конденсаторе;

q m – амплитудное значение заряда на конденсаторе;

β =R /2L – коэффициент затухания,

здесь R – сопротивление контура;

L – индуктивность катушки;

– циклическая частота колебаний;

здесь ω 0 – собственная частота колебаний;

α – начальная фаза колебаний.

Период электромагнитных колебаний:

,

где С – емкость конденсатора;

L – индуктивность катушки;

R – сопротивление контура.

Если сопротивление контура мало, что (R /2L ) 2 <<1/LC , то период колебаний:

Длина волны:

где v – скорость распространения волны;

T – период колебаний.

Уравнение плоской волны:

ξ = A cos (ωt-kx),

где A – амплитуда;

ω – циклическая частота;

– волновое число.

Уравнение сферической волны:

,

где A – амплитуда;

ω – циклическая частота;

k – волновое число;

r – расстояние от центра волны до рассматриваемой точки среды.

? Свободные гармонические колебания в контуре

Идеальный контур – электрическая цепь, состоящая из последовательно соединенного конденсатора емкостью С и катушки индуктивности L. По гармоническому закону будут меняться напряжение на обкладках конденсатора и ток в катушке индуктивности.

? Гармонический осциллятор. Пружинный, физический и математический маятники, их периоды колебаний

Гармонический осциллятор- любая физическая система, совершающая колебания. Классические осцилляторы - пружинный, физический и математический маятники. Пружинный маятник - груз массой m , подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы. Т = . Физический маятник - твердое тело произвольной формы, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести. Т = . Математический маятник – изолированная система, состоящая из материальной точки массой m , подвешенной на нерастяжимой невесомой нити длиной L , и колеблющейся под действием силы тяжести. Т = .

? Свободные незатухающие механические колебания (уравнение, скорость, ускорение, энергия). Графическое изображение гармонических колебаний.

Колебания называются свободными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему. Величина меняется по закону синуса или косинуса. , S - смещение от положения равновесия, А –амплитуда, w 0 - циклическая частота, –начальная фаза колебаний. Скорость , ускорение . Энергия полная – Е = . Графически – с помощью синусоиды или косинусоиды.

? Понятие о колебательных процессах. Гармонические колебания и их характеристики. Период, амплитуда, частота и фаза колебаний. Графическое изображение гармонических колебаний.

Периодические процессы, повторяющиеся со временем, называют колебательными. Периодические колебания, при которых координата тела меняется со временем по закону синуса или косинуса, называются гармоническими. Период - время одного колебания. Амплитуда – максимальное смещение точки от положения равновесия. Частота – число полных колебаний в единицу времени. Фаза - величина, стоящая под знаком синуса или косинуса. Уравнение: , здесь S - величина, характеризующая состояние колеблющейся системы, - циклическая частота. Графически – с помощью синусоиды или косинусоиды.

? Затухающие колебания. Дифференциальное уравнение этих колебаний. Логарифмический декремент затухания, время релаксации, добротность.

Колебания, амплитуда которых со временем уменьшается, например, за счет силы трения. Уравнение: , здесь S - величина, характеризующая состояние колеблющейся системы, - циклическая частота, -коэффициент затухания. Логарифмический декремент затухания , где N – число колебаний, совершенных за время уменьшения амплитуды в N раз. Время релаксации t- в течение которого амплитуда уменьшается в е раз. Добротность Q= .

? Незатухающие вынужденные колебания. Дифференциальное уравнение этих колебаний. Что называют резонансом? Амплитуда и фаза вынужденных колебаний.

Если потери энергии колебаний, приводящие к их затуханию, полностью компенсировать, устанавливаются незатухающие колебания. Уравнение: . Здесь правая часть – меняющееся по гармоническому закону внешнее воздействие. Если собственная частота колебаний системы совпадает с внешней, имеет место резонанс - резкое возрастание амплитуды системы. Амплитуда , .

? Опишите сложение колебаний одинакового направления и одинаковой частоты, взаимоперпендикулярных колебаний. Что такое биения?

Амплитуда результирующего колебания, получающегося при сложении двух гармонических колебаний одинакового направления и одинаковой частоты , здесь А – амплитуды, j - начальные фазы. Начальная фаза результирующего колебания . Взаимоперпендикулярные колебания – уравнение траектории , здесь А и В амплитуды складываемых колебаний, j-разность фаз.

? Охарактеризуйте релаксационные колебания; автоколебания.

Релаксационные – автоколебания, резко отличающиеся по форме от гармонических, благодаря значительному рассеянию энергии в автоколебательных системах (трение в механических системах). Автоколебания – незатухающие колебания, поддерживаемые внешними источниками энергии при отсутствии внешней переменной силы. Отличие от вынужденных – частота и амплитуда автоколебаний определяются свойствами самой колебательной системы. Отличие от свободных колебаний – отличаются независимостью амплитуды от времени и от начального кратковременного воздействия, возбуждающего процесс колебаний. Пример автоколебательной системы –часы.

? Волны (основные понятия). Продольные и поперечные волны. Стоячая волна. Длина волны, связь ее с периодом и частотой.

Процесс распространения колебаний в пространстве называют волной. Направление переноса волной энергии колебаний – это направление движения волны. Продольная – колебание частиц среды происходит в направлении распространения волны. Поперечная - колебания частиц среды происходит перпендикулярно направлению распространения волны. Стоячая волна - образуется при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами, а в случае поперечных волн и одинаковой поляризацией. Длина волны - расстояние, на которое волна распространяется за один период. ( длина волны, v - скорость волны, Т - период колебаний)

? Принцип суперпозиции (наложения) волн. Групповая скорость и ее связь с фазовой скоростью.

Принцип суперпозиции – при распространении в линейной среде нескольких волн каждая распространяется так, будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов. Групповая скорость – скорость движения группы волн, образующих в каждый момент времени в пространстве локализованный волновой пакет. Скорость перемещения фазы волны – фазовая скорость. В недиспергированной среде они совпадают.

? Электромагнитная волна и ее свойства. Энергия электромагнитных волн.

Электромагнитная волна – электромагнитные колебания, распространяющиеся в пространстве. Экспериментально получены Герцем в 1880 г. Свойства- могут распространяться в средах и вакууме, в вакууме равна с, в средах меньше, поперечны, E и B взаимноперпендикулярны и перпендикулярны направлению распространения. Интенсивность увеличивается с ростом ускорения излучающей заряженной частицы, в определенных условиях проявляются типичные волновые свойства – дифракции и пр. Объемная плотность энергии .

Оптика

Основные формулы оптики

Скорость света в среде:

где c – скорость света в вакууме;

n – показатель преломления среды.

Оптическая длина пути световой волны:

L = ns ,

где s – геометрическая длина пути световой волны в среде с показателем преломления n.

Оптическая разность хода двух световых волн:

∆ = L 1 – L 2 .

Зависимость разности фаз от оптической разности хода световых волн:

где λ – длина световой волны.

Условие максимального усиления света при интерференции:

∆ = k λ ( = 0, 1, 2, …) .

Условие максимального ослабления света:

Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки:

∆ = 2d ,

где d – толщина пленки;

n – показатель преломления пленки;

I i – угол преломления света в пленке.

Радиус светлых колец Ньютона в отраженном свете:

r k = , (k = 1, 2, 3, …),

где k – номер кольца;

R – радиус кривизны.

Радиус темных колец Ньютона в отраженном свете:

r k = .

Угол φ отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели, определяется из условия

a sinφ = (k = 0, 1, 2, 3, … ),

где a – ширина щели;

k – порядковый номер максимума.

Угол φотклонения лучей, соответствующий максимуму (светлая полоса) при дифракции света на дифракционной решетке, определяется из условия

d sinφ = (k = 0, 1, 2, 3, …),

где d – период дифракционной решетки.

Разрешающая способность дифракционной решетки:

R = = kN ,

где ∆λ – наименьшая разность длин волн двух соседних спектральных линий (λ и λ+∆λ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки;

N – полное число щелей решетки.

Формула Вульфа – Брэггов:

2d sin θ = κ λ,

где θ – угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле);

d – расстояние между атомными плоскостями кристалла.

Закон Брюстера:

tg ε B = n 21 ,

где ε B – угол падения, при котором отразившийся от диэлектрика луч полностью поляризован;

n 21 – относительный показатель преломления второй среды относительно первой.

Закон Малюса:

I = I 0 cos 2 α,

где I 0 – интенсивность плоскополяризованного света, падающего на анализатор;

I – интенсивность этого света после анализатора;

α – угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора (если колебания электрического вектора падающего света совпадают с этой плоскостью, то анализатор пропускает данный свет без ослабления).

Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:

а) φ = αd (в твердых телах),

где α – постоянная вращения;

d – длина пути, пройденного светом в оптически активном веществе;

б) φ = [α]pd (в растворах),

где [α] – удельное вращение;

p – массовая концентрация оптически активного вещества в растворе.

Давление света при нормальном падении на поверхность:

,

где Е е – энергетическая освещенность (облученность);

ω – объемная плотность энергии излучения;

ρ– коэффициент отражения.

4.2. Понятия и определения раздела «оптика»

? Интерференции волн. Когерентность. Условие максимума и минимума.

Интерференция – взаимное усиление или ослабление когерентных волн при их наложении (когерентные – имеющие одинаковую длину и постоянную разность фаз в точке их наложения).

Максимум ;

минимум .

Здесь D-оптическая разность хода, l-длина волны.

? Принцип Гюйгенса-Френеля. Явление дифракции. Дифракция на щели, дифракционная решетка.

Принцип Гюйгенса-Френеля –каждая точка пространства, которой достигла в данный момент времени распространяющаяся волна, становится источником элементарных когерентных волн. Дифракция – огибание волнами препятствий, если размер препятствия сравним с длиной волны, отклонения света от прямолинейного распространения. Дифракция на щели – в параллельных лучах. На препятствие падает плоская волна, дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути прошедшего через препятствие света. На экране получается «дифракционное изображение» удаленного источника света. Дифракционная решетка – система параллельных щелей равной ширины, лежащих в одной плоскости, разделенных равными по ширине непрозрачными промежутками. Используется для разложения света в спектр и измерения длин волн.

? Дисперсия света (нормальная и аномальная). Закон Бугера. Смысл коэффициента поглощения.

Дисперсия света – зависимость абсолютного показателя преломления вещества n от частоты ν (или длины волны λ) падающего на вещество света (). Скорость света в вакууме не зависит от частоты, поэтому в вакууме дисперсии нет. Нормальная дисперсия света - если показатель преломления монотонно возрастает с увеличением частоты (убывает с увеличением длины волны). Аномальная дисперсия – если показатель преломления монотонно убывает с увеличением частоты (возрастает с увеличением длины волны). Следствие дисперсии – разложение белого света в спектр при его преломлении в веществе. Поглощение света в веществе описывается законом Бугера

I 0 и I – интенсивности плоской монохроматической световой волны на входе и выходе слоя поглощающегося вещества толщиной х , a - коэффициент поглощения, зависит от длины волны, для разных веществ различен.

? Что называют поляризацией волн? Получение поляризованных волн. Закон Малюса.

Поляризация заключается в приобретении преимущественной ориентации направления колебаний в поперечных волнах. Упорядоченность в ориентации векторов напряженностей электрических и магнитных полей электромагнитной волны в плоскости, перпендикулярной направлению распространения светового луча. E , B -перпендикулярны. Естественный свет можно преобразовать в поляризованный с помощью поляризаторов. Закон Малюса (I 0 – прошедший через анализатор, I – прошедший через поляризатор).

? Корпускулярно – волновой дуализм. Гипотеза де Бройля.

Исторически были выдвинуты две теории света: корпускулярная – светящиеся тела испускают частицы-корпускулы (доказательство – излучение черного тела, фотоэффект) и волновая – светящееся тело вызывает в окружающей среде упругие колебания, распространяющиеся подобно звуковым волнам в воздухе (доказательство – явления интерференции, дифракции, поляризации света). Гипотеза Бройля – корпускулярно-волновые свойства присущи не только фотонам, но и частицам, имеющим массу покоя – электронам, протонам, нейтронам, атомам, молекулам. ? Фотоэффект. Уравнение Эйнштейна.

Фотоэффект- явление взаимодействия света с веществом, в результате которого энергия фотонов передается электронам вещества. Уравнение: (энергия фотона расходуется на работу выхода электрона и сообщение электрону кинетической энергии)

Период.

Периодом T называется промежуток времени, в течение которого система совершает одно полное колебание:

N - число полных колебаний за время t .

Частота.

Частота ν - число колебаний в единицу времени:

Единица частоты - 1 герц (Гц) = 1 с -1

Циклическая частота:

Уравнение гармонического колебания:

x - смещение тела от положения. X m - амплитуда, то есть максимальное смещение, (ωt + φ 0) - фаза колебаний, Ψ 0 - его начальная фаза.

Скорость.

При φ 0 = 0:

Ускорение.

При φ 0 = 0:

Свободные колебания.

Свободными называются колебания, возникающие в механической системе (осцилляторе) при единичном отклонении её от положения равновесия, имеющие собственную частоту ω 0 , задаваемую только параметрами системы, и затухающие со временем из-за наличия трения.

Математический маятник.

Частота:

l - длина маятника, g - ускорение свободного падения.

Максимальную кинетическую энергию маятник имеет в момент прохождения положения равновесия:

Пружинный маятник.

Частота:

k - жёсткость пружины, m - масса груза.

Максимальную потенциальную энергию маятник имеет при максимальном смещении:

Вынужденные колебания.

Вынужденными называют колебания, возникающие в колебательной системе (осцилляторе) под действием периодически меняющейся внешней силы.

Резонанс.

Резонанс - резкое увеличение амплитуды X m вынужденных колебаний при совпадении частоты ω вынуждающей силы с частотой ω 0 собственных колебаний системы.

Волны.

Волны - это колебания вещества (механические) или поля (электромагнитные), распространяющиеся в пространстве с течением времени.

Скорость волны.

Скорость распространения волны υ - скорость передачи энергии колебания. При этом частицы среды колеблются около положения равновесия, а не движутся с волной.

Длина волны.

Длина волны λ - расстояние, на которое распространяется колебание за один период:

Единица длины волны - 1 метр (м).

Частота волны:

Единица частоты волны - 1 герц(Гц).

Темы кодификатора ЕГЭ: гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания - это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания - это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия - это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание . Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела - это величина его наибольшего отклонения от положения равновесия.

Период колебаний - это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний - это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них - синус и косинус - являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания - это колебания, при которых координата зависит от времени по гармоническому закону:

(1)

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому - амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .

Величина называется циклической частотой . Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда

(2)

(3)

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1) :

График функции (1) , выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1 .

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:

График гармонических колебаний в этом случае представлен на рис. 2 .

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:

График колебаний представлен на рис. 3 .

Рис. 3. Закон синуса

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1) . Дифференцируем это равенство:

. (4)

Теперь дифференцируем полученное равенство (4) :

. (5)

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :

. (6)

Это соотношение называется уравнением гармонических колебаний . Его можно переписать и в таком виде:

. (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением . Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

Решением уравнения (7) является всякая функция вида (1) с произвольными ;

Никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6) , (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий - по начальным значениям координаты и скорости.

Пружинный маятник.

Пружинный маятник - это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4 ). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

. (8)

Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то . Знаки и всё время противоположны, поэтому закон Гука можно записать так:

Тогда соотношение (8) принимает вид:

Мы получили уравнение гармонических колебаний вида (6) , в котором

Циклическая частота колебаний пружинного маятника, таким образом, равна:

. (9)

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

. (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10) .

Математический маятник.

Математический маятник - это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5 ). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

и спроектируем его на ось :

Если маятник занимает положение как на рисунке (т. е. ), то:

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

Итак, при любом положении маятника имеем:

. (11)

Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11) :

Это - уравнение гармонических колебаний вида (6) , в котором

Следовательно, циклическая частота колебаний математического маятника равна:

. (12)

Отсюда период колебаний математического маятника:

. (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания , если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6 ).

Вынужденные колебания - это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7 .

Рис. 7. Резонанс

Мы видим, что вблизи частоты наступает резонанс - явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .

Гармонические колебания происходят по закону:

x = A cos(ωt + φ 0),

где x – смещение частицы от положения равновесия, А – амплитуда колебаний, ω – круговая частота, φ 0 – начальная фаза, t – время.

Период колебаний T = .

Скорость колеблющейся частицы:

υ = = – A ω sin (ωt + φ 0),

ускорение a = = – A ω 2 cos (ωt + φ 0).

Кинетическая энергия частицы, совершающей колебательное движение: E k = =
sin 2 (ωt + φ 0).

Потенциальная энергия:

E n =
cos 2 (ωt + φ 0).

Периоды колебаний маятников

– пружинного T =
,

где m – масса груза, k – коэффициент жесткости пружины,

– математического T = ,

где l – длина подвеса, g – ускорение свободного падения,

– физического T =
,

где I – момент инерции маятника относительно оси, проходящей через точку подвеса, m – масса маятника, l – расстояние от точки подвеса до центра масс.

Приведенная длина физического маятника находится из условия: l np = ,

обозначения те же, что для физического маятника.

При сложении двух гармонических колебаний одной частоты и одного направления получается гармоническое колебание той же частоты с амплитудой:

A = A 1 2 + A 2 2 + 2A 1 A 2 cos(φ 2 – φ 1)

и начальной фазой: φ = arctg
.

где А 1 , A 2 – амплитуды, φ 1 , φ 2 – начальные фазы складываемых колебаний.

Траектория результирующего движения при сложении взаимноперпендикулярных колебаний одной частоты:

+ – cos (φ 2 – φ 1) = sin 2 (φ 2 – φ 1).

Затухающие колебания происходят по закону:

x = A 0 e - β t cos(ωt + φ 0),

где β – коэффициент затухания, смысл остальных параметров тот же, что для гармонических колебаний, А 0 – начальная амплитуда. В момент времени t амплитуда колебаний:

A = A 0 e - β t .

Логарифмическим декрементом затухания называют:

λ = ln
= βT ,

где Т – период колебания: T = .

Добротностью колебательной системы называют:

Уравнение плоской бегущей волны имеет вид:

y = y 0 cos ω(t ± ),

где у – смещение колеблющейся величины от положения равновесия, у 0 – амплитуда, ω – круговая частота, t – время, х – координата, вдоль которой распространяется волна, υ – скорость распространения волны.

Знак «+» соответствует волне, распространяющейся против оси X , знак «–» соответствует волне, распространяющейся по оси Х .

Длиной волны называют ее пространственный период:

λ = υ T ,

где υ –скорость распространения волны, T –период распространяющихся колебаний.

Уравнение волны можно записать:

y = y 0 cos 2π (+).

Стоячая волна описывается уравнением:

y = (2y 0 cos ) cos ωt.

В скобки заключена амплитуда стоячей волны. Точки с максимальной амплитудой называются пучностями,

x п = n ,

точки с нулевой амплитудой – узлами,

x у = (n + ) .

Примеры решения задач

Задача 20

Амплитуда гармонических колебаний равна 50 мм, период 4 с и начальная фаза . а) Записать уравнение этого колебания; б) найти смещения колеблющейся точки от положения равновесия при t =0 и при t = 1,5 с; в) начертить график этого движения.

Решение

Уравнение колебания записывается в виде x = a cos(t +  0).

По условию известен период колебаний. Через него можно выразить круговую частоту  = . Остальные параметры известны:

а) x = 0,05 cos(t + ).

б) Смещение x при t = 0.

x 1 = 0,05 cos= 0,05 = 0,0355 м.

При t = 1,5 c

x 2 = 0,05 cos( 1,5 + )= 0,05 cos  = – 0,05 м.

в) график функцииx =0,05cos (t + ) выглядит следующим образом:

Определим положение нескольких точек. Известны х 1 (0) и х 2 (1,5), а также период колебаний. Значит, через t = 4 c значение х повторяется, а через t = 2 c меняет знак. Между максимумом и минимумом посередине – 0 .

Задача 21

Точка совершает гармоническое колебание. Период колебаний 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда ее смещение от положения равновесия равно 25 мм.

Решение

1 способ. Записываем уравнение колебания точки:

x = 0,05 cos  t , т. к.  = =.

Находим скорость в момент времени t :

υ = = – 0,05 cos  t.

Находим момент времени, когда смещение равно 0,025 м:

0,025 = 0,05 cos  t 1 ,

отсюда cos t 1 = , t 1 = . Подставляем это значение в выражение для скорости:

υ = – 0,05  sin = – 0,05  = 0,136 м/c.

2 способ. Полная энергия колебательного движения:

E =
,

где а – амплитуда,  – круговая частота, m – масса частицы.

В каждый момент времени она складывается из потенциальной и кинетической энергии точки

E k = , E п = , но k = m  2 , значит, E п =
.

Запишем закон сохранения энергии:

= +
,

отсюда получаем: a 2  2 = υ 2 +  2 x 2 ,

υ = 
= 
= 0,136 м/c.

Задача 22

Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия Е = 3∙10 -7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 2,25∙10 -5 Н?

Решение

Полная энергия точки, совершающей гармонические колебания, равна: E =
. (13)

Модуль упругой силы выражается через смещение точек от положения равновесия x следующим образом:

F = k x (14)

В формулу (13) входят масса m и круговая частота , а в (14) – коэффициент жесткости k . Но круговая частота связана с m и k :

 2 = ,

отсюда k = m  2 и F = m  2 x . Выразив m  2 из соотношения (13) получим: m  2 = , F = x .

Откуда и получаем выражение для смещения x : x = .

Подстановка числовых значений дает:

x =
= 1,5∙10 -2 м = 1,5 см.

Задача 23

Точка участвует в двух колебаниях с одинаковыми периодами и начальными фазами. Амплитуды колебаний А 1 = 3 см и А 2 = 4 см. Найти амплитуду результирующего колебания, если: 1) колебания происходят в одном направлении; 2) колебания взаимно перпендикулярны.

Решение

Если колебания происходят в одном направлении, то амплитуда результирующего колебания определится как:

где А 1 и А 2 – амплитуды складываемых колебаний,  1 и  2 –начальные фазы. По условию начальные фазы одинаковы, значит  2 –  1 = 0, а cos 0 = 1.

Следовательно:

A =
=
= А 1 +А ­ 2 = 7 см.

Если колебания взаимно перпендикулярны, то уравнение результирующего движения будет:

cos( 2 –  1) = sin 2 ( 2 –  1).

Так как по условию  2 –  1 = 0, cos 0 = 1, sin 0 = 0, то уравнение запишется в виде:
=0,

или
=0,

или
.

Полученное соотношение между x и у можно изобразить на графике. Из графика видно, что результирующим будет колебание точки на прямой MN . Амплитуда этого колебания определится как: A =
= 5 см.

Задача 24

Период затухающих колебаний Т =4 с, логарифмический декремент затухания  = 1,6 , начальная фаза равна нулю. Смещение точки при t = равно 4,5 см. 1) Написать уравнение этого колебания; 2) Построить график этого движения для двух периодов.

Решение

Уравнение затухающих колебаний с нулевой начальной фазой имеет вид:

x = A 0 e -  t cos2 .

Для подстановки числовых значений не хватает величин начальной амплитуды А 0 и коэффициента затухания .

Коэффициент затухания можно определить из соотношения для логарифмического декремента затухания:

 = Т .

Таким образом  = = = 0,4 с -1 .

Начальную амплитуду можно определить, подставив второе условие:

4,5 см = A 0
cos 2= A 0
cos =A 0
.

Отсюда находим:

A 0 = 4,5∙

(см) = 7,75 см.

Окончательно уравнение движения:

x = 0,0775
cost.

Задача 25

Чему равен логарифмический декремент затухания математического маятника, если за t = 1 мин амплитуда колебаний уменьшилась в два раза? Длина маятника l = 1 м.

Решение

Логарифмический декремент затухания можно найти из соотношения: = Т ,

где  – коэффициент затухания, Т – период колебаний. Собственная круговая частота математического маятника:

 0 =
= 3,13 с -1 .

Коэффициент затухания колебаний можно определить из условия: A 0 = A 0 e -  t ,

t = ln2 = 0,693 ,

 =
= 0,0116c -1 .

Поскольку  <<  0 , то в формуле  =
можно пренебречь по сравнению с  0 и период колебаний определить по формуле: T = = 2c.

Подставляем  и Т в выражение для логарифмического декремента затухания и получаем:

 = T = 0,0116 с -1 ∙ 2 с = 0,0232.

Задача 26

Уравнение незатухающих колебаний дано в виде x = 4 sin600 t см.

Найти смещение от положения равновесия точки, находящейся на расстоянии l = 75 см от источника колебаний, через t = 0,01 с после начала колебаний. Скорость распространения колебаний υ = 300 м/с.

Решение

Запишем уравнение волны, распространяющейся от данного источника: x = 0,04 sin 600 (t – ).

Находим фазу волны в данный момент времени в данном месте:

t – = 0,01 –= 0,0075 ,

600 ∙ 0,0075 = 4,5 ,

sin 4,5 = sin = 1.

Следовательно, смещение точки x = 0,04 м, т.е. на расстоянии l =75 см от источника в момент времени t = 0,01 c смещение точки максимально.

Список литературы

Волькенштейн В.С . Сборник задач по общему курсу физики. – СПб.: СпецЛит, 2001.

Савельев И.В . Сборник вопросов и задач по общей физике. – М.: Наука, 1998.

Колебательным называется любое периодически повторяющееся движение. Поэтому зависимости координаты и скорости тела от времени при колебаниях описываются периодическими функциями времени. В школьном курсе физики рассматриваются такие колебания, в которых зависимости и скорости тела представляют собой тригонометрические функции , или их комбинацию, где - некоторое число. Такие колебания на-зываются гармоническими (функции и часто называют гармоническими функциями). Для решения задач на колебания, входящих в программу единого государственного экзамена по физике, нужно знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний. Дадим эти определения и свяжем перечисленные величины с параметрами зависимости координаты тела от времени , которая в случае гармонических колебаний всегда может быть представлена в виде

где , и - некоторые числа.

Амплитудой колебаний называется максимальное отклонение колеблющегося тела от положения равновесия. Поскольку максимальное и минимальное значение косинуса в (11.1) равно ±1, то амплитуда колебаний тела, совершающего колебания (11.1), равна величине . Период колебаний - это минимальное время, через которое движение тела повторяется. Для зависимости (11.1) период можно установить из следующих соображений. Косинус - периодическая функция с периодом . Поэтому движение полностью повторяется через такое значение , что . Отсюда получаем

Круговой (или циклической) частотой колебаний называется число колебаний, совершаемых за единиц времени. Из формулы (11.3) заключаем, что круговой частотой является величина из формулы (11.1).

Фазой колебаний называется аргумент тригонометрической функции, описывающей зависимость координаты от времени. Из формулы (11.1) видим, что фаза колебаний тела, движение которого описывается зависимостью (11.1), равна . Значение фазы колебаний в момент времени = 0 называется начальной фазой. Для зависимости (11.1) начальная фаза колебаний равна величине . Очевидно, начальная фаза колебаний зависит от выбора начала отсчета времени (момента = 0), которое всегда является условным. Изменением начала отсчета времени начальная фаза колебаний всегда может быть «сделана» равной нулю, а синус в формуле (11.1) «превращен» в косинус или наоборот.

В программу единого государственного экзамена входит также знание формул для частоты колебаний пружинного и математического маятников. Пружинным маятником принято называть тело, которое может совершать колебания на гладкой горизонтальной поверхности под действием пружины, второй конец которой закреплен (левый рисунок). Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити (правый рисунок). Название этой системы – «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического ) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника

где - длина нити, - ускорение свободного падения. Рассмотрим применение этих определений и законов на примере решения задач.

Чтобы найти циклическую частоту колебаний груза в задаче 11.1.1 найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 м 28 с - это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1 c -1 (ответ 2 ). В задаче 11.1.2 груз за 600 с совершил 60 колебаний, поэтому частота колебаний - 0,1 с -1 (ответ 1 ).

Чтобы понять, какой путь пройдет груз за 2,5 периода (задача 11.1.3 ), проследим за его движением. Через период груз вернется назад в точку максимального отклонения, совершив полное колебание. Поэтому за это время груз пройдет расстояние, равное четырем амплитудам: до положения равновесия - одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону - вторая, назад в положение равновесия - третья, из положения равновесия в начальную точку - четвертая. За второй период груз снова пройдет четыре амплитуды, а за оставшиеся половину периода - две амплитуды. Поэтому пройденный путь равен десяти амплитудам (ответ 4 ).

Величина перемещения тела - расстояние от начальной точки до конечной. За 2,5 периода в задаче 11.1.4 тело успеет совершить два полных и половину полного колебания, т.е. окажется на максимальном отклонении, но с другой стороны от положения равновесия. Поэтому величина перемещения равна двум амплитудам (ответ 3 ).

По определению фаза колебаний - это аргумент тригонометрической функции, которой описывается зависимость координаты колеблющегося тела от времени. Поэтому правильный ответ в задаче 11.1.5 - 3 .

Период - это время полного колебания. Это значит, что возвращение тела назад в ту же точку, из которой тело начало движение, еще не означает, что прошел период: тело должно вернуться в ту же точку с той же скоростью. Например, тело, начав колебания из положения равновесия, за период успеет отклониться на максимальную величину в одну сторону, вернуться назад, отклонится на максимум в другую сторону и снова вернуться назад. Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения (задача 11.1.6 ) тело затрачивает четвертую часть периода (ответ 3 ).

Гармоническими называются такие колебания, при которых зависимость координаты колеблющегося тела от времени описывается тригонометрической (синус или косинус) функцией времени. В задаче 11.1.7 таковыми являются функции и , несмотря на то, что входящие в них параметры обозначены как 2 и 2 . Функция же - тригонометрическая функция квадрата времени. Поэтому гармоническими являются колебания только величин и (ответ 4 ).

При гармонических колебаниях скорость тела изменяется по закону , где - амплитуда колебаний скорости (начало отсчета времени выбрано так, чтобы начальная фаза колебаний равнялась бы нулю). Отсюда находим зависимость кинетической энергии тела от времени
(задача 11.1.8 ). Используя далее известную тригонометрическую формулу, получаем

Из этой формулы следует, что кинетическая энергия тела изменяется при гармонических колебаниях также по гармоническому закону, но с удвоенной частотой (ответ 2 ).

За соотношением между кинетической энергий груза и потенциальной энергией пружины (задача 11.1.9 ) легко проследить из следующих соображений. Когда тело отклонено на максимальную величину от положения равновесия, скорость тела равна нулю, и, следовательно, потенциальная энергия пружины больше кинетической энергии груза. Напротив, когда тело проходит положение равновесия, потенциальная энергия пружины равна нулю, и, следовательно, кинетическая энергия больше потенциальной. Поэтому между прохождением положения равновесия и максимальным отклонением кинетическая и потенциальная энергия один раз сравниваются. А поскольку за период тело четыре раза проходит от положения равновесия до максимального отклонения или обратно, то за период кинетическая энергия груза и потенциальная энергия пружины сравниваются друг с другом четыре раза (ответ 2 ).

Амплитуду колебаний скорости (задача 11.1.10 ) проще всего найти по закону сохранения энергии. В точке максимального отклонения энергия колебательной системы равна потенциальной энергии пружины , где - коэффициент жесткости пружины, - амплитуда колебаний. При прохождении положения равновесия энергия тела равна кинетической энергии , где - масса тела, - скорость тела при прохождении положения равновесия, которая является максимальной скоростью тела в процессе колебаний и, следовательно, представляет собой амплитуду колебаний скорости. Приравнивая эти энергии, находим

(ответ 4 ).

Из формулы (11.5) заключаем (задача 11.2.2 ), что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ 1 ).

Часы - это колебательный процесс, который используется для измерения интервалов времени (задача 11.2.3 ). Слова часы «спешат» означают, что период этого процесса меньше того, каким он должен быть. Поэтому для уточнения хода этих часов необходимо увеличить период процесса. Согласно формуле (11.5) для увеличения периода колебаний математического маятника необходимо увеличить его длину (ответ 3 ).

Чтобы найти амплитуду колебаний в задаче 11.2.4 , необходимо представить зависимость координаты тела от времени в виде одной тригонометрической функции. Для данной в условии функции это можно сделать с помощью введения дополнительного угла. Умножая и деля эту функцию на и используя формулу сложения тригонометрических функций, получим

где - такой угол, что . Из этой формулы следует, что амплитуда колебаний тела - (ответ 4 ).