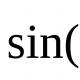Графические задачки. Графические задачи по физике и графическое решение задач

Все построения в процессе графического счисления выполняют при помощи прокладочного инструмента:

навигационного транспортира,

параллельной линейки,

циркуля-измерителя,

чертежного циркуля с карандашом.

Линии наносят простым карандашом и убирают мягкой резинкой.

Снять с карты координаты заданной точки. Наиболее точно эту задачу можно выполнить с помощью циркуля-измерителя. Для снятия широты одну ножку циркуля ставят в заданную точку, а другую так подводят к ближайшей параллели, чтобы описанная циркулем дуга ее касалась.

Не изменяя угла раствора ножек циркуля, подносят его к вертикальной рамке карты и ставят одну ножку на параллель, до которой измерялось расстояние.
Другую ножку ставят на внутреннюю половину вертикальной рамки в сторону заданной точки и снимают отсчет широты с точностью до 0,1 наименьшего деления рамки. Долготу заданной точки определяют таким же образом, только расстояние измеряют до ближайшего меридиана, а отсчет долготы снимают по верхней или нижней рамке карты.

Нанести точку по заданным координатам. Работу выполняют обычно с помощью параллельной линейки и циркуля-измерителя. Линейку прикладывают к ближайшей параллели и отодвигают одну ее половину до заданной широты. Затем раствором циркуля берут расстояние от ближайшего меридиана до заданной долготы по верхней или нижней рамке карты. Одну ножку циркуля ставят у среза линейки на тот же меридиан, а другой ножкой делают слабый укол также у среза линейки в сторону заданной долготы. Место укола и будет являться заданной точкой

Измерить расстояние между двумя точками на карте или отложить известное расстояние от заданной точки. Если расстояние между точками небольшое и может быть измерено одним раствором циркуля, то ножки циркуля ставят в одну и другую точки, не меняя его раствора, приставляют к боковой рамке карты в той же примерно широте, в которой лежит измеряемое расстояние.

Большое расстояние при измерении разбивают на части. Каждую часть расстояния измеряют милями в широте данного участка. Можно также раствором циркуля взять с боковой рамки карты "круглое" число миль (10,20 и т. д.) и сосчитать, сколько раз уложить это число по всей измеряемой линии.
При этом мили снимают с боковой рамки карты примерно против середины измеряемой линии. Остаток расстояния измеряют обычным способом. Если нужно отложить от заданной точки небольшое расстояние, то его снимают циркулем с боковой рамки карты и откладывают на проложенной линии.
Расстояние берут с рамки примерно в широте заданной точки с учетом его направления. Если откладываемое расстояние большое, то берут с рамки карты примерно против середины заданного расстояния 10, 20 миль, и т.д. и откладывают нужное число раз. От последней точки отмеряют остаток расстояния.

Измерить направление проложенной на карте линии истинного курса или пеленга. Параллельную линейку прикладывают к линии на карте и приставляют к срезу линейки транспортир.
Транспортир перемещают вдоль линейки до тех пор, пока его центральный штрих не совпадет с каким-либо меридианом. Деление на транспортире, через которое проходит тот же меридиан, соответствует направлению курса или пеленга.
Так как на транспортире нанесены два отсчета, то при измерении направления проложенной линии следует учитывать четверть горизонта, в которой лежит заданное направление.

Проложить от заданной точки линию истинного курса или пеленга. При выполнении этой задачи используют транспортир и параллельную линейку. Транспортир накладывают на карту так, чтобы его центральный штрих совпал с каким-либо меридианом.

Затем транспортир поворачивают в ту и другую сторону до тех пор, пока с тем же меридианом не совпадет штрих дуги, соответствующей отсчету заданного курса или пеленга. К нижнему срезу линейки транспортира прикладывают параллельную линейку, и, убрав транспортир, раздвигают ее, подводя к заданной точке.

По срезу линейки в нужную сторону проводят линию. Перенести точку с одной карты на другую. С карты снимают направление и расстояние до заданной точки от какого-либо маяка или другого ориентира, нанесенного на обе карты.
На другой карте, проложив от этого ориентира нужное направление и отложив по нему расстояние, получают заданную точку. Эта задача является комбинированной

Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.

Рассмотрим задачу линейного программирования с двумя переменными и :
(1.1) ;
(1.2)
Здесь , есть произвольные числа. Задача может быть как на нахождение максимума (max), так и на нахождение минимума (min). В системе ограничений могут присутствовать как знаки , так и знаки .

Построение области допустимых решений

Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.

Так, первое неравенство
(1.2.1)
определяет полуплоскость, ограниченную прямой . С одной стороны от этой прямой , а с другой стороны . На самой прямой . Чтобы узнать, с какой стороны выполняется неравенство (1.2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку. Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).

Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.

Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.

Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых. Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.

Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).

Нахождение экстремума целевой функции

Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.

Теперь мы можем искать экстремум целевой функции
(1.1) .

Для этого выбираем любое число и строим прямую
(3) .
Для удобства дальнейшего изложения считаем, что эта прямая проходит через ОДР. На этой прямой целевая функция постоянна и равна . такая прямая называется линией уровня функции . Эта прямая разбивает плоскость на две полуплоскости. На одной полуплоскости
.
На другой полуплоскости
.
То есть с одной стороны от прямой (3) целевая функция возрастает. И чем дальше мы отодвинем точку от прямой (3), тем больше будет значение . С другой стороны от прямой (3) целевая функция убывает. И чем дальше мы отодвинем точку от прямой (3) в другую сторону, тем меньше будет значение . Если мы проведем прямую, параллельную прямой (3), то новая прямая также будет линией уровня целевой функции, но с другим значением .

Таким образом, чтобы найти максимальное значение целевой функции, надо провести прямую, параллельную прямой (3), максимально удаленную от нее в сторону возрастания значений , и проходящую хотя бы через одну точку ОДР. Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.

Если ОДР неограниченна, то может возникнуть случай, когда такую прямую провести нельзя. То есть как бы мы ни удаляли прямую от линии уровня (3) в сторону возрастания (убывания) , то прямая всегда будет проходить через ОДР. В этом случае может быть сколь угодно большим (малым). Поэтому максимального (минимального) значения нет. Задача решений не имеет.

Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.

Также может встретиться случай, когда прямая параллельна одной из граней ОДР. Тогда прямая проходит через две вершины многоугольника ОДР. Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
.
Задача имеет бесконечно много решений. Решением является любая точка, расположенная на отрезке между точками и , включая сами точки и .

Пример решения задачи линейного программирования графическим методом

Условие задачи

Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида - 10 м, третьего вида - 16 м. Выпуск одного изделия типа А приносит доход 400 ден. ед., одного изделия типа В - 300 ден. ед.

Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.

Решение

Пусть переменные и означают количество произведенных платьев моделей А и В, соответственно. Тогда количество израсходованной ткани первого вида составит:
(м)
Количество израсходованной ткани второго вида составит:
(м)
Количество израсходованной ткани третьего вида составит:
(м)
Поскольку произведенное количество платьев не может быть отрицательным, то
и .
Доход от произведенных платьев составит:
(ден. ед.)

Тогда экономико-математическая модель задачи имеет вид:

Решаем графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 7) и (10,5; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 10) и (10; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (8; 0).

Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.

(П1.1) .
При .
При .
Проводим прямую через точки (0; 4) и (3; 0).

Далее замечаем, что поскольку коэффициенты при и целевой функции положительны (400 и 300), то она возрастает при увеличении и . Проводим прямую, параллельную прямой (П1.1), максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку четырехугольника OABC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

Решение задачи: ;

Ответ

.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.

Пример 2

Условие задачи

Решить задачу линейного программирования графическим методом.

Решение

Решаем графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 6) и (6; 0).

Строим прямую .
Отсюда .
При .
При .
Проводим прямую через точки (3; 0) и (7; 2).

Строим прямую .
Строим прямую (ось абсцисс).

Область допустимых решений (ОДР) ограничена построенными прямыми. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.

Строим произвольную линию уровня целевой функции, например,
.
При .
При .
Проводим прямую линию уровня через точки (0; 6) и (4; 0).
Поскольку целевая функция увеличивается при увеличении и , то проводим прямую, параллельную линии уровня и максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку треугольника АВC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

Решение задачи: ;

Ответ

Пример отсутствия решения

Условие задачи

Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.

Решение

Решаем задачу графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (2,667; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 3) и (6; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (3; 0) и (6; 3).

Прямые и являются осями координат.

Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.

Строим произвольную линию уровня целевой функции, например,
(П3.1) .
При .
При .
Проводим прямую через точки (0; 7) и (7; 0).
Поскольку коэффициенты при и положительны, то возрастает при увеличении и .

Чтобы найти максимум, нужно провести параллельную прямую, максимально удаленную в сторону возрастания , и проходящую хотя бы через одну точку области ABCDE. Однако, поскольку область неограниченна со стороны больших значений и , то такую прямую провести нельзя. Какую бы прямую мы не провели, всегда найдутся точки области, более удаленные в сторону увеличения и . Поэтому максимума не существует. можно сделать сколь угодно большой.

Ищем минимум. Проводим прямую, параллельную прямой (П3.1) и максимально удаленную от нее в сторону убывания , и проходящую хотя бы через одну точку области ABCDE. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Минимальное значение целевой функции:

Ответ

Максимального значения не существует.
Минимальное значение
.

К задачам этого типа относятся такие, в которых все или часть данных заданы в виде графических зависимостей меж­ду ними. В решении таких задач можно выделить следующие этапы:

2 этап - выяснить из приведенного графика, между какими величинами представлена связь; выяснить, какая физическая величина является независимой, т. е. аргументом; какая величина является зависимой, т. е. функцией; определить по виду графика, какая это зависимость; выяснить, что требуется - определить функцию или аргумент; по возможности, записать уравнение, которое описывает приведенный график;

3 этап - отметить на оси абсцисс (или ординат) заданное значение и восстановить перпендикуляр до пересечения с графиком. Опустить перпендикуляр из точки пересечения на ось ординат (или абсцисс) и определить значение искомой величины;

4 этап - оценить полученный результат;

5 этап - записать ответ.

Прочитать график координаты – это значит, что из графика следует определить: начальную координату и скорость движения; записать уравнение координаты; определить время и место встречи тел; определить, в какой момент времени тело имеет данную координату; определить координату, которую тело имеет в указанный момент времени.

Задачи четвертого типа - экспериментальные . Это задачи, в которых для нахождения неизвестной величины требуется часть данных измерить опытным путем. Предлагается следующий порядок работы:

2 этап - определить, какое явление, закон лежат в основе опыта;

3 этап - продумать схему опыта; определить перечень приборов и вспомогательных предметов или оборудования для проведения эксперимента; продумать последовательность проведения эксперимента; в случае необходимости разработать таблицу для регистрации результатов эксперимента;

4 этап - выполнить эксперимент и результаты записать в таблицу;

5 этап - сделать необходимые расчеты, если это требуется согласно условию задачи;

6 этап - обдумать полученные результаты и записать ответ.

Частные алгоритмы для решения задач по кинематике и динамике имеют следующий вид.

Алгоритм решения задач по кинематике:

2 этап - выписать численные значения заданных величин; выразить все величины в единицах «СИ»;

3 этап - сделать схематический чертеж (траекторию движения, векторы скорости, ускорения, перемещения и т.д.);

4 этап - выбрать систему координат (при этом следует выбрать такую систему, чтобы уравнения были несложными);

5 этап - составить для данного движения основные уравнения, которые отражают математическую связь между изображенными на схеме физическими величинами; число уравнений должно быть равно числу неизвестных величин;

6 этап - решить составленную систему уравнений в общем виде, в буквенных обозначениях, т.е. получить расчетную формулу;

7 этап - выбрать систему единиц измерения («СИ»), подставить в расчетную формулу вместо букв наименования единиц, произвести действия с наименованиями и проверить, получается ли о результате единица измерения искомой величины;

8 этап - выразить все заданные величины в избранной системе единиц; подставить в расчетные формулы и вычислить значения искомых величин;

9 этап - проанализировать решение и сформулировать ответ.

Сравнение последовательности решения задач по динамике и кинематике дает возможность увидеть, что некоторые пункты являются общими для обоих алгоритмов, это помогает лучше их запомнить и более успешно применять при решении задач.

Алгоритм решения задач по динамике:

2 этап - записать условие задачи, выразив все величины в единицах «СИ»;

3 этап - сделать чертеж с указанием все сил, действующих на тело, векторы ускорений и системы координат;

4 этап - записать уравнение второго закона Ньютона в векторном виде;

5 этап - записать основное уравнение динамики (уравнение второго закона Ньютона) в проекциях на оси координат с учетом направления осей координат и векторов;

6 этап - найти все величины, входящие в эти уравнения; подставить в уравнения;

7 этап - решить задачу в общем виде, т.е. решить уравнение или систему уравнений относительно неизвестной величины;

8 этап - проверить размерность;

9 этап - получить численный результат и соотнести его с реальными значениями величин.

Алгоритм решения задач на тепловые явления:

1 этап - внимательно прочитать условие задачи, выяснить, сколько тел участвует в теплообмене и какие физические процессы происходят (например, нагревание или охлаждение, плавление или кристаллизация, парообразование или конденсация);

2 этап - кратко записать условие задачи, дополняя необходимыми табличными величинами; все величины выразить в системе «СИ»;

3 этап - записать уравнение теплового баланса с учетом знака количества теплоты (если тело получает энергию, то ставят знак «+», если тело отдает - знак «-»);

4 этап - записать необходимые формулы для расчета количества теплоты;

5 этап - записать полученное уравнение в общем виде относительно искомых величин;

6 этап - произвести проверку размерности полученной величины;

7 этап - вычислить значения искомых величин.

РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫ

Работа № 1

ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ

Основные положения:

Механическое движение – изменение положения тела относительно других тел или изменение положения частей тела со временем.

Материальная точка – тело, размерами которого можно пренебречь в данной задаче.

Физические величины бывают векторные и скалярные.

Вектором называется величина, характеризующаяся числовым значением и направлением (сила, скорость, ускорение и т.д.).

Скаляром называется величина, характеризующаяся только числовым значением.(масса, объем, время и т.д.).

Траектория - линия, вдоль которой движется тело.

Пройденный путь - длина траектории движущегося тела, обозначение - l , единица измерения в системе СИ: 1 м, скаляр (имеет модуль, но не имеет направления), однозначно не определяет конечное положение тела.

Перемещение - вектор, соединяющий начальное и последующее положения тела, обозначение - S, единица измерения в СИ: 1 м, вектор (имеет модуль и направление), однозначно определяет конечное положение тела.

Скорость – векторная физическая величина, равная отношению перемещения тела к промежутку времени, за которое это перемещение произошло.

Механическое движение бывает поступательным, вращательным и колебательным.

Поступательным движением называют движение, при котором любая прямая, жестко связанная с телом, перемещается, оставаясь параллельной самой себе. Примерами поступательного движения являются движение поршня в цилиндре двигателя, движение кабин «чертова колеса» и т.д. При поступательном движении все точки твердого тела описывают одинаковые траектории и в каждый момент времени имеют одинаковые скорости и ускорения.

Вращательным движением абсолютно твердого тела называют такое движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения , и описывают окружности, центры которых лежат на этой оси (роторы турбин, генераторов и двигателей).

Колебательное движение – это движение, периодически повторяющееся в пространстве с течением времени.

Системой отсчета называется совокупность тела отсчета, системы координат и способа измерения времени.

Тело отсчета – любое тело, выбираемое произвольно и условно считаемое неподвижным, относительно которого изучается расположение и движение других тел.

Система координат состоит из выделенных в пространстве направлений – осей координат, пересекающихся в одной точке, называемой началом отсчета и выбранного единичного отрезка (масштаба). Система координат нужна для количественного описания движения.

В декартовой системе координат положение точки А в данный момент времени по отношению к этой системе определяется тремя координатами х, у и z, или радиусом-вектором .

Траекторией движения материальной точки называется линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным и криволинейным .

Движение называется равномерным, если скорость материальной точки с течением времени не изменяется.

Действия с векторами:

Скорость – векторная величина, показывающая направление и быстроту перемещения тела в пространстве.

Всякому механическому движению присущ абсолютный и относительный характер .

Абсолютный смысл механического движения состоит в том, что если два тела сближаются или удаляются друг от друга, то они будут сближаться или удаляться в любой системе отсчета.

Относительность механического движения заключается в том, что:

1) бессмысленно говорить о движении, не указав тело отсчета;

2) в разных системах отсчета одно и то же движение может выглядеть по-разному.

Закон сложения скоростей : Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости этого же тела относительно подвижной системы отсчета и скорости подвижной системы относительно неподвижной.

Контрольные вопросы

1. Определение механического движения (примеры).

2. Виды механического движения (примеры).

3. Понятие материальной точки (примеры).

4. Условия, при выполнении которых тело можно считать материальной точкой.

5. Поступательное движение (примеры).

6. Что включает в себя система отсчета?

7. Что такое равномерное движение (примеры)?

8. Что называется скоростью?

9. Закон сложения скоростей.

Выполните задания:

1. Улитка проползла прямолинейно 1 м, затем сделала поворот, описав четверть окружности радиусом 1 м, и проползла далее перпендикулярно первоначальному направлению движения еще 1 м. Сделать чертеж, рассчитать пройденный путь и модуль перемещения, на чертеже не забыть показать вектор перемещения улитки.

2. Движущийся автомобиль сделал разворот, описав половину окружности. Сделать чертеж, на котором указать путь и перемещение автомобиля за треть времени разворота. Во сколько раз путь, пройденный за указанный промежуток времени, больше модуля вектора соответствующего перемещения?

3. Может ли спортсмен на водных лыжах двигаться быстрее катера? Может ли катер двигаться быстрее лыжника?

Эксперты доказывают преимущество технического образования перед гуманитарным, доказывают, что Россия остро нуждается в высококвалифицированных инженерах и технических специалистах, и эта тенденция сохранится не только в 2014 году, но и на протяжении последующих лет. По мнению специалистов по подбору персонала, если страну будет ждать экономический рост в ближайшие годы (а предпосылки к этому есть), то весьма вероятно, что российская образовательная база "не потянет" многие отрасли (высокие технологии, промышленность). "На данный момент на рынке труда ощущается острый дефицит специалистов в области инженерно-технических специальностей, в области IT: программистов, разработчиков ПО. Востребованными остаются инженеры практически всех специализаций. В то же время рынок перенасыщен юристами, экономистами, журналистами, психологами", - говорит генеральный директор Кадрового агентства уникальных специалистов Екатерина Крупина. Аналитики, делая долгосрочные прогнозы до 2020 года, уверены: спрос на технические специальности будет с каждым годом стремительно расти. Актуальность проблемы. Следовательно, актуально качество подготовки к ЕГЭ по физике. Решающим является овладение методами решения физических задач. Разновидностью физических задач являются графические задачи. 1) Решение и анализ графических задач позволяют понять и запомнить основные законы и формулы по физике. 2) В КИМах для проведения ЕГЭ по физике включены задания с графическим содержанием.

Скачать работу с презентацией.

ЦЕЛЬ ПРОЕКТНОЙ РАБОТЫ:

Изучение типов графических задач, разновидностей, особенностей и методов решения.

ЗАДАЧИ РАБОТЫ:

1. Изучение литературы о графических заданиях; 2. Изучение материалов ЕГЭ (распространенность и уровень сложности графических заданий); 3. Исследование общего и особенного графических задач из разных разделов физики, степени сложности. 4. Изучение методов решения; 5. Проведение социологического опроса среди учащихся и учителей школы.

Физическая задача

В методической и учебной литературе под учебными физическими задачами понимают целесообразно подобранные упражнения, главное назначение которых заключается в изучении физических явлений, формировании понятий, развитии физического мышления учащихся и привитии им умений применять свои знания на практике.

Научить учащихся решать физические задачи - одна из сложнейших педагогических проблем. Я считаю данную проблему очень актуальной. Мой проект имеет своей целью решить две задачи:

1. Помочь в обучении школьников умению решать графические задачи;

2. Привлечь учащихся к данному виду работы.

Решение и анализ задачи позволяют понять и запомнить основные законы и формулы физики, создают представление об их характерных особенностях и границах применение. Задачи развивают навык в использовании общих законов материального мира для решения конкретных вопросов, имеющих практическое и познавательное значение. Умение решать задачи является лучшим критерием оценки глубины изучения программного материала и его усвоения.

В исследованиях по выявлению степени усвоения учащимися отдельных операций, входящих в умение решать задачи, установлено, что 30-50% учащихся различных классов указывают на отсутствие у них такого умения.

Неумение решать задачи является одной из основных причин снижения успеха в изучении физики. Проведенные исследования показали, что неумение самостоятельно решать задачи является основной причиной нерегулярного выполнения домашних заданий. Только небольшая часть учащихся овладевает умением решать задачи, рассматривает как одно из важнейших условий повышения качества знаний по физике.

Такое состояние в практике обучения можно объяснить отсутствием четких требований к формированию данного умения, отсутствие внутренних побудительных мотивов и познавательного интереса у учащихся.

Решение задач в процессе обучения физики имеет многогранные функции:

• Овладение теоретическими знаниями.
• Овладение понятиями о физических явлениях и величинах.
• Умственного развития, творческого мышления и специальных способностей учащихся.
• Знакомит учащихся с достижениями науки и техники.
• Воспитывает трудолюбие, настойчивость, волю, характер, целеустремленность.
• Является средством контроля за знаниями, умениями и навыками учащихся.

Графическая задача.

Графические задачи - это такие задачи, в процессе решения которых используют графики, диаграммы, таблицы, чертежи и схемы.

Например:

1. Построить график пути равномерного движения, если v = 2 м/с или равноускоренного при v 0 =5 м/с и а = 3 м/с 2 .

2. Какие явления характеризует каждая часть графика…

3. Какое тело движется быстрее

4. На каком участке тело двигалось быстрее

5. Определить по графику скорости величину, пройденного пути.

6. На каком участке движения тело покоилось. Скорость увеличивалась, уменьшалась.

Решение графических задач способствует уяснению функциональной зависимостью между физическими величинами, привитию навыков работы с графиками, развитию умения работать с масштабами.

По роли графиков в решении задач их можно подразделить на два вида: - задачи, ответ на вопрос которых может быть найден в результате построения графика; - задачи, ответ на вопрос которых может быть найден с помощью анализа графика.

Графические задачи могут быть комбинированными с экспериментальными.

Например:

С помощью мензурки с водой определить вес деревянного бруска…

Подготовка к решению графических задач.

Для решения графических задач ученик должен знать различные виды функциональных зависимостей, что означает пересечение графиков с осями, графиков между собой. Нужно понимать чем отличаются зависимости, например, x = x 0 + vt и x = v 0 t + at 2 /2 или x =x m sinω 0 t и x = - x m sinω 0 t; x =x m sin(ω 0 t+ α) и x =x m cos (ω 0 t+ α) и т.д.

План подготовки должен содержать следующие разделы:

· а) Повторить графики функций (линейной, квадратичной, степенной) · б) Выяснить - какую роль играют графики в физике, какую информацию несут. · в) Систематизировать физические задачи по значимости графиков в них. · г) Изучить методы и приемы анализа физических графиков · д) Выработать алгоритм решения графических задач по различным разделам физики · е) Выяснить общую закономерность в решении графических задач. Для овладения методами решения задач необходимо решать большое количество разнотипных задач, соблюдая принцип - «От простого к сложному». Начиная с простых, осваивать методы решения, сравнивать, обобщать разные задачи как на основе графиков, так и на основе таблиц, диаграмм, схем. Следует обращать внимание на обозначение величин по координатным осям (единицы физических величин, наличие дольных или кратных приставок), масштаб, вид фукциональной зависимости (линейная, квадратичная, логарифмическая, тригонометрическая и т.п.), на углы наклона графиков, точки пересечения графиков с координатными осями или графиков между собой. Особенно внимательно необходимо подходить к задачам с заложенными «ощибками», так же к задачам с фотографиями шкал измерительных приборов. В этом случае нужно правильно определить цену деления измерительных приборов и безошибочно считать значения измеряемых величин. В задачах на геометрическую оптику особенно важно аккуратно и точно делать построение лучей и определить пересечения их с осями и между собой.

Как решать графические задачи

Овладение общим алгоритмом решения физических задач

1. Осуществление анализа условия задачи с выделением задач системы, явлений и процессов, описанных в задаче, с определением условий их протекания

2. Осуществление кодирования условия задачи и процесса решения на различных уровнях:

а) краткая запись условия задачи;

б) выполнение рисунков, электрических схем;

в) выполнение чертежей, графиков, векторных диаграмм;

г) запись уравнения (системы уравнений) или построение логического умозаключения

3. Выделение соответствующего метода и способов решения конкретной задачи

4. Применение общего алгоритма для решения задач различных видов

Решение задачи начинается с чтения условия. Нужно убедиться в том, что все термины и понятия в условии ясны для учащихся. Непонятные термины выясняются после первичного чтения. Одновременно необходимо выделить, какое явление, процесс или свойство тел описывается в задаче. Затем задача читается повторно, но уже с выделением данных и искомых величин. И только после этого осуществляют краткую запись условия задачи.

Составление плана

Действие ориентировки позволяет осуществить вторичный анализ воспринятого условия задачи, в результате выполнения которого выделяются физические теории, законы, уравнений, объясняющие конкретную задачу. Затем выделяются методы решения задач одного класса и находится оптимальный метод решения данной задачи. Результатом деятельности учащихся является план решения, который включает цепочку логических действий. Правильность выполнения действий по составлению плана решения задачи контролируется.

Процесс решения

Во-первых, необходимо уточнить содержание известных уже действий. Действие ориентации на данном этапе предполагает еще раз выделение метода решения задачи и уточнение вида решаемой задачи по способу задания условия. Последующим действием является планирование. Планируется способ решения задачи, тот аппарат (логический, математический, экспериментальный) с помощью которого возможно осуществить дальнейшее ее решение.

Анализ решения

Последний этап процесса решения задачи заключается в проверке полученного результата. Осуществляется он снова теми же действиями, но содержание действий изменяется. Действие ориентации - это выяснение сущности того, что необходимо проверить. Например, результатами решения могут быть значения величин коэффициентов, физических постоянных характеристик механизмов и машин, явлений и процессов.

Результат, полученный в ходе решения задачи, должен быть правдоподобным и соответствовать здравому смыслу.

Распространенность графических задач в КИМах в заданиях ЕГЭ

Изучение материалов ЕГЭ ряда лет (2004 - 2013г.г.) показало, в заданиях ЕГЭ по различным разделам физики распространены графические задачи по различным разделам физики. В заданиях А: по механике - 2-3 по молекулярной физике - 1 по термодинамике - 3 по электродинамике - 3-4 по оптике - 1-2 по квантовой физике - 1 по атомной и ядерной физике - 1 В заданиях В: по механике -1 по молекулярной физике - 1 по термодинамике - 1 по электродинамике - 1 по оптике - 1 по квантовой физике - 1 по атомной и ядерной физике - 1 В заданиях С: по механике - по молекулярной физике - по термодинамике - 1 по электродинамике - 1 по оптике - 1 по квантовой физике - по атомной и ядерной физике - 1

Наши исследования

А. Анализ ошибок при решении графических задач

Анализ решения графических задач показал, что встречаются следующие распостранённые ошибки:

Ошибки в чтении графиков;

Ошибки в действиях с векторными величинами;

Ошибки при анализе графиков изопроцессов;

Ошибки на графическую зависимость электрических величин;

Ошибки при построении с применением законов геометрической оптики;

Ошибки в графических заданиях на квантовые законы и фотоэффект;

Ошибки на применение законов атомной физики.

Б. Социологический опрос

Для того, чтобы выяснить как учащиеся школы осведомлены о графических задачах, мы провели социологический опрос.

Ученикам и учителям нашей школы мы предлагали следующие вопросы анкеты:

1. 1. Что такое графическая задача?

а) задачи с рисунками;

б) задачи, содержащие схемы, диаграммы;

в) не знаю.

1. 2. Для чего графические задачи?

б) для развития умения строить графики;

в) не знаю.

3. Можете ли решать графические задачи?

а) да; б) нет; в) не уверен;

4. Хотите ли научиться решать графические задачи?

А) да; б) нет; в) затрудняюсь ответить.

Было опрошено 50 человек. В результате опроса были получены следующие данные:

ВЫВОДЫ:

1. В результате работы над проектом «Графические задачи» изучили особенности графических задач.
2. Изучили особенности методики решения графических задач.
3. Провели анализ характерных ошибок.
4. Провели социологический опрос.

Рефлексия деятельности:

1. Нам было интересно работать над проблемой графических задач.
2. Мы научились проводить исследовательскую деятельность, сопоставлять и сравнивать результаты исследований.
3. Мы выяснили, что владение методами решения графических задач необходимо для понимания физических явлений.
4. Мы выяснили, что владение методами решения графических задач необходимо для успешной сдачи ЕГЭ.

Графические головоломки

1. Соединить четыре точки тремя линиями, не отрывая руки и вернуться в исходную точку.

. .

1. Соединить девять точек четырьмя линиями, не отрывая руки.

. . .

. . .

. . .

1. Покажите, как нужно разрезать прямоугольник со строками 4 и 9 единиц на две равные части, чтобы при сложении их получился квадрат.

1. Куб, окрашенный со всех сторон, распилили, как показано на рис.

а) Сколько получится кубиков

Совсем не окрашенных?

б) У скольких кубиков окрашенной

Будет одна грань?

в) У скольких кубиков будут

Окрашены две грани?

г) У скольких кубиков окрашенными

Будут три грани?

д) У скольких кубиков окрашенными

Будут четыре грани?

Ситуативные, конструкторские

И технологические задачи

Задача. Шарики трех размеров под действием собственного веса непрерывным потоком скатываются по наклонному лотку. Как осуществить непрерывную сортировку шариков на группы в зависимости от размеров?

Решение. Необходимо разработать конструкцию калибрующего приспособления.

Шарики, покинув лоток, скатываются далее по клиновидному калибру. В том месте, где ширина щели совпадает с диаметром шарика, он проваливается в соответствующий приемник.

Задача. Герои одного фантастического рассказа берут в полет вместо тысяч необходимых запчастей синтезатор-машину, умеющую делать все. При посадке на другую планету корабль повреждается. Нужно 10 одинаковых деталей для ремонта. Тут выясняется, что синтезатор делает все в одном экземпляре. Как найти выход из этой ситуации?

Решение. Необходимо заказать синтезатору произвести самого себя. Второй синтезатор выдает им еще один и т.д.

Ответы на графические головоломки.

1. . .

2. . . .

. . .

. . .